Энергия заряженного тела и электрического поля
5. Для использования граничных условий необходимо повторить пункты с 1 по 3 для второй среды, получив еще две константы.
Литература: [1], глава 2, §15; [3], глава 1, §11.
Основной блок задач
1. Дан шар радиуса ![]() , равномерно заряженный по объему с плотностью заряда
, равномерно заряженный по объему с плотностью заряда ![]() . Вычислить потенциал, создаваемый шаром в точке наблюдения
. Вычислить потенциал, создаваемый шаром в точке наблюдения ![]() при условии:
при условии:
· а) точка ![]() лежит вне шара
лежит вне шара 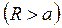 ;
;
· б) точка ![]() лежит внутри шара
лежит внутри шара 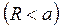 .
.
2. Рассчитайте потенциал, создаваемый бесконечно длинным цилиндром радиуса ![]() , заряженного по объему с плотностью
, заряженного по объему с плотностью 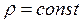 .
.
3. Дана бесконечная пластинка, ориентированная в пространстве перпендикулярно оси ![]() . Толщина пластинки
. Толщина пластинки ![]() , она заряжена с объемной плотностью заряда
, она заряжена с объемной плотностью заряда ![]() . Точка наблюдения находится на расстоянии
. Точка наблюдения находится на расстоянии ![]() от центра пластины. Найдите потенциал электрического поля в точке наблюдения.
от центра пластины. Найдите потенциал электрического поля в точке наблюдения.
Дополнительный блок задач
4. В сферических координатах объемная плотность заряда внутри шара радиуса ![]() симметрична относительно оси
симметрична относительно оси ![]() и имеет вид
и имеет вид 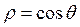 , где
, где ![]() – полярный угол, а начало координат совпадает с центром шара. Найдите потенциал и напряженность электрического поля, создаваемого этим шаром, во всем пространстве. Учтите, что в данном случае потенциал не зависит от азимутального угла
– полярный угол, а начало координат совпадает с центром шара. Найдите потенциал и напряженность электрического поля, создаваемого этим шаром, во всем пространстве. Учтите, что в данном случае потенциал не зависит от азимутального угла ![]() .
.
5. Бесконечный цилиндр радиуса ![]() заряжен равномерно по своей длине. Объемная плотность заряда
заряжен равномерно по своей длине. Объемная плотность заряда 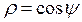 , где
, где ![]() – полярный угол, а ось
– полярный угол, а ось ![]() цилиндрической системы координат совпадает с осью цилиндра. Найдите потенциал и напряженность электрического поля, создаваемого этим цилиндром, во всем пространстве.
цилиндрической системы координат совпадает с осью цилиндра. Найдите потенциал и напряженность электрического поля, создаваемого этим цилиндром, во всем пространстве.
6. Найдите распределение объемной плотности ![]() заряда, создавшего в пространстве электрическое поле, потенциал которого в сферических координатах имеет вид:
заряда, создавшего в пространстве электрическое поле, потенциал которого в сферических координатах имеет вид:
· 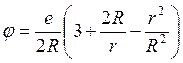 при
при ![]() ;
;
· 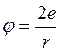 при
при ![]() ; где
; где ![]() и
и ![]() – некоторые постоянные.
– некоторые постоянные.
7. Потенциал ![]() электрического поля в сферических координатах имеет вид
электрического поля в сферических координатах имеет вид 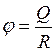 при
при ![]() и
и 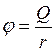 при
при ![]() , где
, где ![]() и
и ![]() – постоянные. Найдите распределение заряда, создавшего это поле
– постоянные. Найдите распределение заряда, создавшего это поле
Замечание: Условия упражнений 4-7 записаны в системе СГСЭ, однако методы решения остаются теми же.
Практическое занятие №4
Энергия заряженного тела и электрического поля
Краткие теоретические сведения
Выражение для работы по перемещению единичного положительного заряда в электрическом поле позволяет получить связь потенциальной энергии заряда ![]() в поле с потенциалом
в поле с потенциалом ![]()
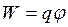 . (4.1)
. (4.1)
Энергия взаимодействия большого числа зарядов рассчитывается по формуле
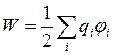 , (4.2)
, (4.2)
где ![]() – потенциал электрического поля в точке расположения заряда
– потенциал электрического поля в точке расположения заряда ![]() . При непрерывном распределении заряда по поверхности или объему от суммирования переходят к интегрированию, например, для распределенного по поверхности заряда энергия равна
. При непрерывном распределении заряда по поверхности или объему от суммирования переходят к интегрированию, например, для распределенного по поверхности заряда энергия равна
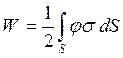 . (4.3)
. (4.3)
Для энергии диполя во внешнем поле можно получить формулу
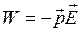 . (4.4)
. (4.4)
От расчета энергии заряженного тела в электрическом поле можно перейти к рассмотрению энергии электрического поля, создаваемого данным заряженным телом


