Теория пластичности

Теория пластичности является одной из основных дисциплин для студентов, обучающихся по направлению " Механика, прикладная математика ".

В соответствии с учебным планом данная дисциплина изучается в течение 7 семестра. Предусмотрено выполнение курсовой работы. Целью данной работы является закрепление общих положений теории в процессе решения конкретных задач. Самостоятельное решение этих задач способствует овладению методами теории пластичности, выработке необходимой интуиции и способности количественно описывать основные механические процессы. В данных методических указаниях приведены примеры заданий к курсовой работе, выполняемой в 7-ом семестре, и подробно описан метод их решения. Необходимые теоретические положения содержатся в курсе лекций по теории пластичности, а также могут быть почерпнуты из учебников (см. список литературы). Отметим, что наряду с типовыми заданиями могут выполняться и задания, содержащие элементы исследования.

1. Цель и задачи КР

Курсовая работа «Решение упругопластической задачи» является обязательным этапом курса «Теория пластичности». КР выполняется в течение седьмого семестра.

Целью КР является углубление теоретических знаний, полученных в процессе обучения, и развитие навыков их применения к решению конкретных задач.

Основные задачи КР:

·  математическая постановка задачи;

·  построение решения упругопластической задачи методом упругих решений;

·  разработка алгоритма решения задач линейной теории упругости, которые необходимо решать в каждой итерации метода упругих решений;

·  составление компьютерной программы;

·  выполнение расчётов и анализ их результатов.

2. Основные требования к КР

Содержание КР

КР включает в себя индивидуальное задание, а также подробное изложение работы, раскрывающее решение основных задач КР (см. предыдущий раздел).

Задание на КР

Задание на КР выдаётся преподавателем. Задание содержит расчётную схему рассчитываемой конструкции (статически неопределимую балку) с указанием необходимых размеров, а также численные значения следующих величин (подробнее см. ниже):

— размеров поперечного сечения b, h;

— модуля Юнга Е и предела текучести материала.

Содержание задания является исходными данными для выполнения КР.

Результаты выполнения КР

В итоге выполнения КР студент должен получить (и обязательно описать в пояснительной записке) решение поставленной задачи, представляющее собой компьютерную программу, которая позволяет:

·  вычислять предельное значение параметра нагрузки;

·  строить эпюры максимальных напряжений (по поперечному сечению и по длине балки) при произвольном значении параметра нагрузки;

·  строить эпюры прогибов при произвольном значении параметра нагрузки, в том числе и после разгрузки.

Оформление КР

КР оформляется в виде пояснительной записки. Программа для компьютера представляется на магнитном носителе, который после защиты КР возвращается студенту.

Пояснительная записка (ПЗ) оформляется в соответствии с общепринятыми требованиями[1]. ПЗ может не содержать введения и списка литературы.

Защита КР

Готовая пояснительная записка сдаётся на проверку преподавателю. Проверенная ПЗ возвращается студенту, который знакомится с замечаниями преподавателя. Студент обязан, по требованию преподавателя, доработать КР (исправить ошибки, доделать незавершённое и т. д.) и вновь сдать ПЗ на проверку. После того, как все существенные, по мнению преподавателя, недочеты работы будут исправлены, студент допускается к её защите. В процессе защиты студент должен продемонстрировать:

·  детальное понимание всех этапов выполнения работы;

·  знание теории;

·  умение решать задачи.

Если в процессе защиты преподаватель убеждается в несамостоятельности студента при выполнении КР, он выдает студенту новое задание.

Студент, не защитивший КР, не допускается к зачету по курсу “Теория пластичности”.

3. Пояснения к основным этапам КР

Расчетная схема

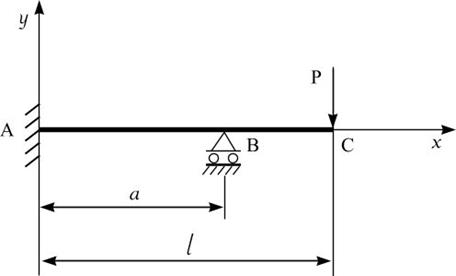
Рис. 1. Статически неопределимая балка

Типичная расчётная схема изображена на рис. 1. Нагрузок может быть несколько (может быть приложена и распределённая нагрузка), но все они изменяются пропорционально одному параметру — параметру нагрузки (в данном случае – это величина нагрузки P).

Поперечное сечение балки – это прямоугольник (рис. 2).

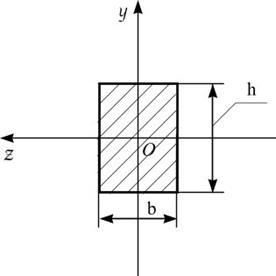
Рис. 2. Поперечное сечение балки. Линия действия нагрузки лежит в плоскости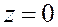

Свойства материала

Материал предполагается упругопластическим, деформации малыми. В упругой области справедлив закон Гука. Материал рассматривается как идеально пластический. В качестве критерия текучести используется критерий Мизеса.

Таким образом, упругопластическое деформирование описывается следующей системой уравнений

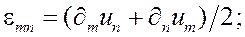
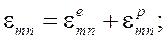
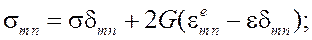
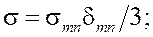
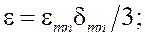
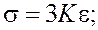
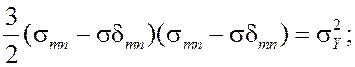
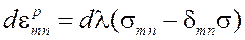(1)

где — тензор деформаций; — вектор перемещений; — оператор дифференцирования; — символ Кронекера; — тензор напряжений; G – модуль сдвига; K – объёмный модуль; 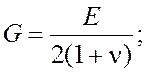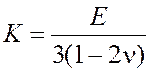; E – модуль Юнга; — коэффициент Пуассона; — предел текучести; — неопределённый множитель, учитывающий условие текучести.

Последние два соотношения выполняются при пластическом деформировании.

В данном случае (изгиб балки) соотношения (1) существенно упрощаются. Согласно гипотезам Бернулли-Эйлера, из компонент тензора напряжений отлична от нуля только одна:. В результате получаются выражения:

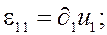
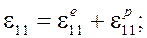
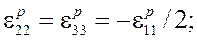
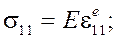
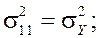
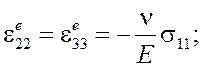
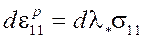(2)

Далее вместо и будем писать и , вместо — писать x , вместо — писать u, а вместо — писать . Приходим к формулам

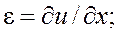
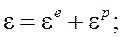
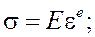
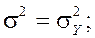
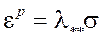(3)

где — неопределённый множитель (последнее соотношение (2) в данном случае интегрируется, так как реализуется простое нагружение).

Разрешающая система уравнений

В соответствии с гипотезой плоских сечений Бернулли-Эйлера

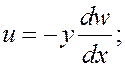
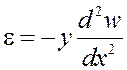(4)

где ордината y отсчитывается от нейтральной оси сечения .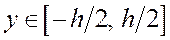

Рассмотрим условия равновесия части балки, левая граница которой находится в сечении с абсциссой x. Действие опоры В учитывается реакцией связи R. Величина R определяется в процессе решения задачи из условия .

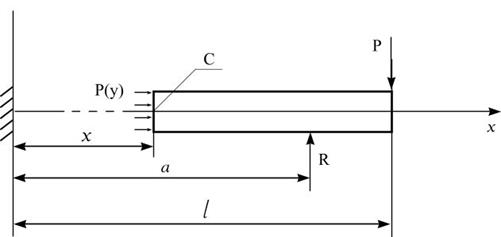
Рис.3. Равновесие части балки

Со стороны отброшенной части балки на рассматриваемую часть действует распределённая по сечению нагрузка .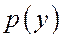

Условия равновесия части балки имеют вид

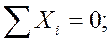
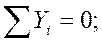
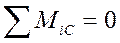(5)

то есть должны быть равны нулю главный вектор и главный момент.

Первое уравнение даёт

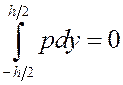(6)

а третье уравнение:

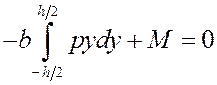(7)

где М – момент внешних сил (изгибающий момент). В данном случае

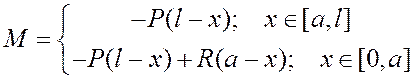(8)

Второе уравнение (5), в соответствии с гипотезами Бернулли-Эйлера, из рассмотрения исключается.

Используем соотношение , где – единичная нормаль (внешняя) к торцовой поверхности в сечении с абсциссой x. Очевидно, что . Следовательно, и уравнения (6) и (7) записываются в виде

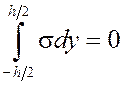
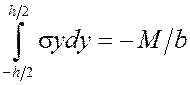; (9)

В предположении, что — нечётная функция y, первое уравнение удовлетворяется тождественно, а второе записывается в виде

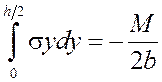(10)

Это уравнение, а также соотношения (3) и (4) являются основными уравнениями задачи. Их решение должно удовлетворять граничным условиям. В данном случае это условия заделки при :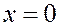

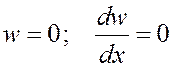(11)

и условия опирания при :

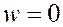(12)

Решение задачи методом упругих решений

Напряжение представляется в виде

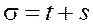(13)

где составляющая t связана c деформациями законом Гука, то есть

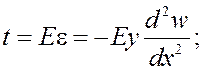
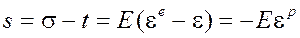(14)

Уравнение (10) преобразуется к виду

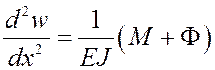(15)

где 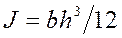— момент инерции поперечного сечения,

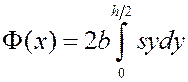(16)

В уравнении (15) M(x) – известная функция (с точностью до констант, определяемых из граничных условий), а Ф(x) – функция определяемая в процессе решения задачи. Уравнение (15) можно представить в интегральном виде

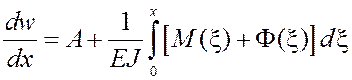(17)

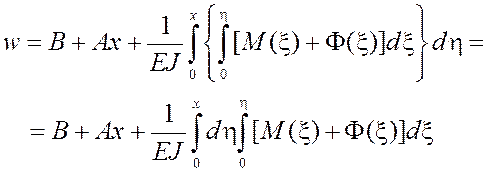(18)

Изменяя порядок интегрирования в выражении (18), получим

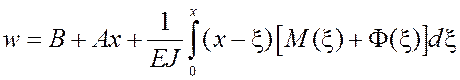(19)

Здесь А, В – константы интегрирования. Выражения (17) и (19) позволяют получить формулы для определения неизвестной постоянной в выражении для изгибающего момента М. Так, в данном случае А=В=0 (см. условия (11)), а условие (12) даёт

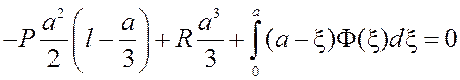(20)

Если функция 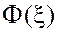известна, то из уравнения (20) находится константа R.

Решение задачи получается следующим образом. Задаётся шаг приращения параметра нагружения (в данном случае ).

Процесс нагружения разбивается на этапы; на очередном этапе нагружения нагрузка увеличивается на величину :

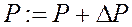(21)

К началу очередного этапа функция Ф(x) известна из расчёта предыдущего этапа (для первого этапа Ф(x)=0 – чисто упругое деформирование). С использованием формул (17), (19) находится неизвестная константа в выражении для М(x) (в данном случае R из уравнения (20)). Теперь по формуле (15) можно определить 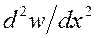в любом сечении балки.

Рассмотрим последовательность дальнейшего расчета. Итак, в некотором сечении балки с абсциссой x известна величина 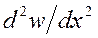. По формуле (14) находится распределение t по толщине балки, и далее по формуле (13) – распределение напряжений (начальные напряжения s известны из расчёта предыдущего этапа; при расчёте первого этапа – упругое деформирование). Если для какого-либо значения y оказывается, что , величина s корректируется таким образом, чтобы выполнялось условие :

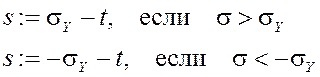(22)

По скорректированным таким образом начальным напряжениям вычисляется функция Ф(х) (по формуле (16)). Далее строится итерационный процесс: с использованием формул (17), (19) находится константа в выражении для М(х), далее по формуле (15) находится 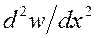, затем по формуле (14) – распределение t по толщине балки и вновь, если это необходимо корректируются значения начальных напряжений и вычисляется функция Ф(х). Интегралы от функции 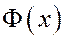в формулах (17), (19), (20) находятся численно. Итерационный процесс продолжается до тех пор, пока приращения начальных напряжений от итерации к итерации не станут пренебрежимо малыми.

После этого выполняется следующий этап нагружения — параметр нагружения увеличивается на величину .

Определение предельной нагрузки

С ростом параметра нагружения скорость сходимости итерационного процесса уменьшается (зона пластического деформирования становится все больше). При некотором предельном параметре нагружения итерационный процесс начинает расходиться — начинается неограниченное пластическое деформирование (пластическое течение). Таким образом, расходимость итерационного процесса свидетельствует о достижении предельной нагрузки.

Определение остаточных деформаций, напряжений, перемещений

Пусть найдено решение упругопластической задачи при некотором значении параметра нагружения. Чтобы определить остаточные напряжения, деформации, перемещения, нужно из полученного решения вычесть решение упругой задачи при том же значении параметра нагружения.

Точность решения задачи

Для оценки точности решения необходимо проводить несколько расчётов с последовательно уменьшающимся значением до тех пор, пока расхождение в найденных величинах предельной нагрузки не станет приемлемым ~.

литература

1. Качанов Л. М. Основы теории пластичности. — М.: Наука, 1969. — 420 с.

2. Клюшников В. Д. Математическая теория пластичности. — М.: Изд-во МГУ, 1979. — 208 с.

3. Малинин Н. Н. Прикладная теория пластичности и ползучести. — М.: Машиностроение, 1968. — 400 с.

4. Соколовский В. В. Теория пластичности. — М.: Высш. школа, 1969. — 608 с.

5. Фрейденталь А., Гейрингер Х. Математические теории неупругой сплошной среды. — М.: ГИФМЛ, 1962. — 431 с.

Рассмотрено на заседании кафедры

Протокол №_____ от "___" ______________ 2012 г.

Зав. кафедрой ____________________ А. А. Маркин

[1] см. «Методические указания по выполнению выпускной квалификационной работы для студентов, обучающихся по направлению 511300 «Механика. Прикладная математика»