ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнФизика и биофизика задачи
ε — угловое ускорение, которое равно (ω1- ω2)/t, т. е.
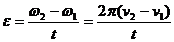
Подставляя в (1) 
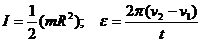
найдем
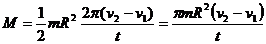(2)
Подставляя в (2) численные значения величин и произведя вычисления,
получим:
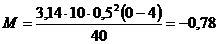Нм.
Знак «минус» показывает, что силы трения оказывают на маховик тормозящее действие.
Ответ: М= -0,78 Нм.
Пример 5
Определить массу т0 молекулы кислорода и число молекул кислорода, содержащихся в объеме V= 1 смЗ, при плотности газа ρ = 1,43 кг/м3.
Дано:
V=1 см3=10-6м3;
М=32·10-3 кг/моль;
ρ = 1,43 кг/м3.
N=?
m0 = ?
Решение
Число молекул массой m равно произведению числа Авогадро NA на число молей v. Поскольку число молей v = т/М, где М— молярная масса, то N=NА т/М. Массу газа можно выразить через плотность и объем: m=Vp, тогда
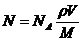. (1)
Подставим в (1) числовые значения величин и произведем вычисления:
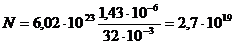молекул.
Массу одной молекулы т0 найдем делением молярной массы на число Авогадро:
;
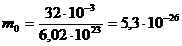кг.
Ответ: N = 2,7·1019молекул; т0 = 5,3·10-26 кг.
Пример 6
1 кг водорода при температуре 27 °С изотермически расширили до двойного объема, а затем изохорно охладили, уменьшив давление в 5 раз. Дать схему процесса в системе координат p, V. Подсчитать изменение внутренней энергии и внешнюю работу газа.
Дано:
i = 5;
т = 1 кг;
М=2·10-3 кг/моль;
T1 = 300 К;
Т2=Т1;
V2= 2V1;
р3 =1/5 р1;
DU = ?
А = ?
Решение
Схема процесса представлена на рис. 3. Внутренняя энергия газа:
,
а изменение внутренней энергии определяется по уравнению:
.
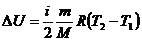При переходе газа из состояния 1 в 2 (см. рис. 3): Т1 = Т2, следовательно,
DU1,2 = 0. (2)
При переходе из состояния 2 в 3 (см. рис. 3):
, (3)
где T2 = Т1
Нужно найти Т3. Напишем уравнение изохорного процесса при переходе газа из состояний 2 и 3:
p2/p3 = Т2/Т3, откуда Т3 = (р3T1) /р2 (4)
Здесь неизвестно p2. Найдем его из уравнения изотермического процесса состояния 1→2:
p1V1= p2V2 и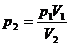 
. (5)
Подставим р2 в выражение (4) для Т3:
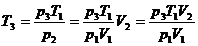. (6)
Тогда
. (7)
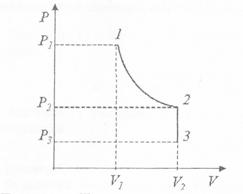
Рис.3
Подставим в (7) числовые значения величин и произведем вычисления:
(Дж)
Следовательно, DU2,3 = -5,99·106 (Дж). Внутренняя энергия газа уменьшилась. Найдем работу газа. Очевидно, что А1,3 = А1,2 + А2,3 = А1,2, так как на участке 2,3: А2,3 = 0 (V2= V3). На участке 1,2 — процесс изотермический,
а .
Подсчитаем:
А = ·8,31·300·ln2 = 8,64·105(Дж) = 0,86МДж.
Ответ: DU2,3 = -5,99 Дж; А = 0,86 МДж.
Пример 7
В вершинах квадрата расположены равные положительные заряды q = 10-8 Кл (рис. 4). В центре квадрата помещен отрицательный заряд q0. Определить значение этого заряда q0, если он уравновешивает силы взаимного отталкивания зарядов q.
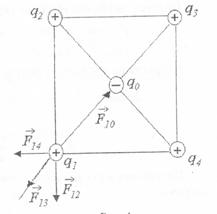
Рис. 4
Дано:
q1=q2 = q3= q4=10-8Кл;
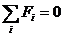
q0 = ?
Решение
Для вычисления q0 используем закон Кулона и принцип суперпозиции. Заряды q1, q2, q3, q4 одинаковы и расположены симметрично. Поэтому рассуждения проводим для одного из них, например q1. Определим условие, при котором заряд q1 находился бы в равновесии с зарядом q0. Силы, которые действуют на заряд q1 со стороны зарядов, q2, q3, q4, q0, обозначим F12, F13, F14, F10 соответственно. Для равновесия заряда q1 надо, чтобы векторная сумма этих сил была бы равна 0:
(1)
Направления этих сил показаны на рис. 4. Переходим от векторного выражения к скалярному, проецируя все силы на направление диагонали квадрата, проходящей через заряд q :
F12cosα + F14cosα + F13 — F10 = 0, (2)
где α = 45°.
По закону Кулона
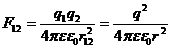, (3)
где r — расстояние между зарядами, равное стороне квадрата;
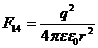; (4)
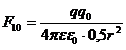, (5)
так как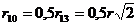 
;
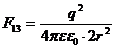, (6)
так как r132 = r2 + r2 = 2r2.
Подставляя (3), (4), (5), (6) в (2), получим:
.
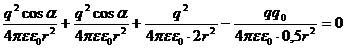Сократив на q и 4πεε0r2, получим:
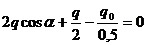, или 4qcosα + q — 4q0 = 0, откуда
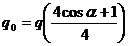. (7)
Подставляя в (7) численные значения величин и произведя вычисления, получим:
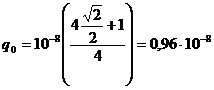Кл.
Ответ: q0 = 0,96·10-8Kл.
Пример 8
ЭДС батареи 6В, внутреннее сопротивление 0,5 Ом. Определить: 1) мощность, развиваемую источником тока; 2) полезную мощность; 3) КПД батареи, если она включена на внешнее сопротивление 1,5 Ом.
Дано:
ε=6В;
r0 = 0,5 Ом;
R = 1,5 0м.
P0 = ?
P = ?
h = ?
Решение
Мощность Р0, развиваемая источником тока, равна Р0 = IE. Так как по закону Ома для полной цепи:
,
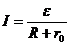то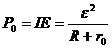 
. (1)
Полезная мощность, мощность, выделяемая на внешнем сопротивлении:
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломная работа