Физика колебаний и волн

«Физика колебаний и волн. Квантовая физика»

Тема I. Волновые процессы

Лекция №1

Общие представления о волновом движении

1. Волновое движение. Волновая функция. Скалярные и векторные волны.

2. Скалярное волновое уравнение. Граничные и начальные условия. Стоячая волна.

3. Бегущая плоская монохроматическая волна и ее основные кинематические характеристики.

4. Комплексная форма записи волновой функции. Формула Эйлера.

5. Сферическая монохроматическая волна.

6. Метод Фурье.

В этом разделе общей физики изучается новый универсальный вид движения материи – волновое движение. Волновое движение осуществляет пространственный перенос временных изменений физических характеристик, а не вещества как в случае механического движения тел. Волновое движение присуще физическим полям, включая гравитационное поле, состоящее из взаимодействующих между собой частиц, описываемой законами квантовой механики.

Наиболее важные и часто встречающиеся волны — упругие волны в газах, жидкостях и твердых телах, волны на поверхности жидкости и электромагнитные волны. Эти волны переносят энергию, импульс, момент импульса и информацию, которые могут передаваться частицам вещества при их взаимодействии.

Для возникновения в некоторой среде волны необходим источник, создающий в данной среде локальное возмущение её параметров, зависящее от времени. Благодаря взаимодействию между соседними элементами среды это возмущение перемещается в среде в виде волны. Энергия волны определяется работой, которую совершает источник при возбуждении волны.

В основу теории линейных волн, для которых выполняется принцип суперпозиции, положен пространственный перенос гармонических колебаний различных физических величин, описываемых известной формулой

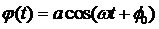, (1.1)

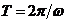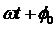где a=const>0 – амплитуда колебаний, — круговая (циклическая) частота, – период колебаний, — начальная фаза и — фаза колебаний.

В качестве модели среды, в которой возможно волновое движение, часто используется множество одинаковых гармонических осцилляторов, распределенных в некоторой пространственной области и взаимодействующих между собой. Благодаря взаимодействию по такой системе осцилляторов возникает перенос колебании. В результате формируется согласованное определенным образом в пространстве и времени коллективное движение большого количества осцилляторов среды, представляющее собой волну.

Данное согласованное движение множества осцилляторов образует волновое поле меняющихся во времени и пространстве физических величин, которое описывается с помощью волновой функции, зависящей от координат и времени. В зависимости от вида волновой функции различают скалярные и векторные волны. Звук в газе и жидкости, переносящий временные изменения давления p, является скалярной волной, а электромагнитные волны, переносящие временные изменения векторов напряженности электрического и магнитного полей, — векторными волнами. Важно отметить, что волновое поле рассматривается как система с бесконечным числом степеней свободы, а его динамика описывается уравнениями в частных производных, которые называются волновыми уравнениями.

Вид волнового уравнения зависит от физической природы волны. В случае механических волн в дискретной или сплошной среде волновое уравнение получается путем применения II-ого закона Ньютона для описания движения макроскопического элемента среды. Простейшее одномерное скалярное волновое уравнение, описывающее механическое волновое движение вдоль оси х в сплошной среде, имеет вид

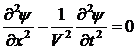. (1.2)

Здесь ψ – волновая функция, определяющая отклонение некоторой физической характеристики макроскопического элемента среды от ее равновесного значения в отсутствие волнового движения, V – постоянная, имеющая размерность скорости и зависящая от параметров среды, и t – время. Уравнение (1.2) описывает свободное распространение волны в пассивной среде без источников, где нет поглощения или усиления волн.

Для нахождения единственного решения уравнения (1.2) при t>0 в некоторой области необходимо в момент времени t=0 задать два начальных условия:

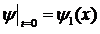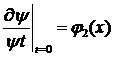, , х1<x<x2 (1.3)

вместе с двумя граничными условиями в точках х=х1 и х=х2.

В случае волны на натянутой струне с закрепленными концами граничные условия принимают вид

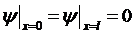, (1.4)

где l – длина струны, координаты х=0 и х=l определяют начало и конец струны соответственно – смещение элемента струны в поперечном направлении.

При граничных условиях (1.4) волновое уравнение (1.2), которое пригодно для описания поперечного волнового движения струны, имеет счетное множество решений в виде

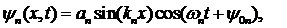(1.5)

которые определяют стоячие волны. Здесь – амплитуда стоячей волны, равная максимальному поперечному отклонению любого элемента струны в области 0<x<l от его равновесного положения,

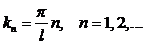(1.6)

– волновое число, с которым связаны длина волны

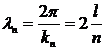(1.7)

и частота

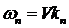. (1.8)

Скорость V, входящая в волновое уравнение (1.2), определяется линейной плотностью струны (масса элемента струны единичной длины) и натяжением струны Т согласно формуле

.

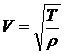Отметим, что при возбуждении произвольной стоячей волны на струне с закрепленными концами на длине струны l,как видно из (1.7), укладывается целое число полуволн . Счетное множество различных решений (1.5) соответствует бесконечному числу степеней свободы волнового поля. Любое волновое движение на струне с закрепленными концами может быть представлено в виде суперпозиции стоячих волн (1.5).

Обобщение одномерного волнового уравнения (1.2) на трехмерный случай выполняется очевидным образом

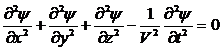. (1.9)

Простейшее решение этого уравнения, описывающее плоскую монохроматическую волну с частотой ω, которая распространяется в направлении, задаваемом единичным вектором , имеет вид

, (1.10)