Геометрический способ приведения системы сил к простейшему виду

F1 = 3 H, F2 = 4 H.

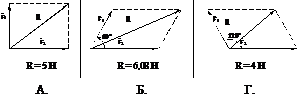
19.

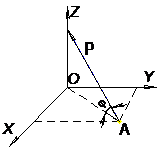
Определите проекцию силы на ось если и

и сила приложена в точке А(3;3;0).

а)Ру = Р;б) Ру = 0,5Р;

в) Ру = ; г) Ру=2Р;

20.

Определите проекцию силы на ось если и

и сила приложена в точке А, координаты которой(3;3;0).

а)Рх = Р;б) Рх = 0,5Р;

в) Рх = ; г) Рх =2Р;

2.Приведение системы сходящихся сил к простейшему виду

План исследования любой системы сил соответствует последовательному решению следующих вопросов:

— как упростить данную систему сил?

— каков простейший вид системы сил?

— каковы условия и уравнения равновесия данной системы сил?

Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке.

Сходящимися составляющими силами называют такие силы, которые в своей совокупности эквиваленты данной силе и приложены в одной точке с данной силой.

Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных координатных плоскостях.

Пусть задана плоская система сил (,,,) (рисунок12)

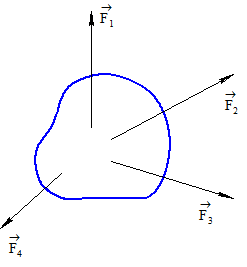
Рисунок 12

Поставим задачу упростить эту систему. Замена сложной системы более простой, ее эквивалентной, называется приведением системы сил к простейшему виду. Докажем, что система сходящихся сил имеет равнодействующую.

2.1 Геометрический способ приведения системы сил к простейшему виду

В случае плоской системы сходящихся сил можно воспользоваться плоским чертежом, откладывая силы в некотором масштабе. Модуль равнодействующей силы и ее направление определяются измерением по чертежу. Такой способ нахождения равнодействующей называется графическим или геометрическим.

На основании следствия из третьей аксиомы силу можно переносить вдоль линии её действия, поэтому систему сходящихся сил всегда можно перенести в одну точку — точку пересечения их линии действия. Выполнив перенос, получим силы ,,,(пучок сил), приложенные в точке О, которая называется точкой схода сил (рисунок 13).

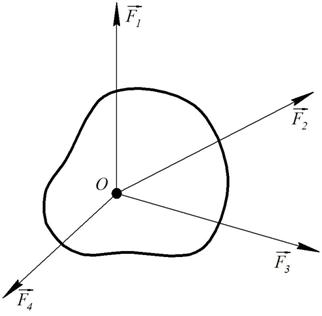
Рисунок 13

Для определения их равнодействующей сложим последовательно все данные силы, используя аксиому параллелограмма сил (рисунок 14).

Две силы и заменим их равнодействующей . В результате получим новую эквивалентную систему сходящихся сил:

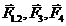(,,,)() (1)

Теперь аналогично заменим две силы иих равнодействующей 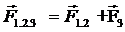(2)

Повторяя подобные построения двух пересекающихся сил, в каждом случае получая новую эквивалентную систему сходящихся сил в том же центре, придем в итоге к одной силе , которая называется равнодействующей системы сходящихся сил или главным вектором системы сходящихся сил.

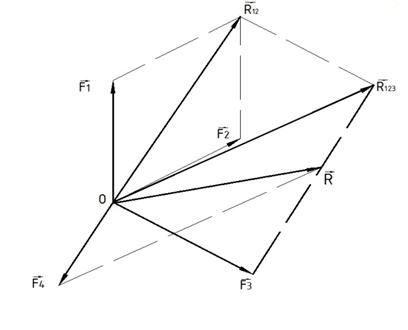
Рисунок 14

Равнодействующая (главный вектор) системы сходящихся сил равна геометрической (векторной) сумме векторов всех этих сил и проходит через точку пересечения линий их действия.

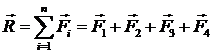(3)

Главный вектор — это геометрическое понятие он существует всегда, а равнодействующая системы сил – понятие физическое и существует не для всякой системы сил.

Построение равнодействующей может быть упрощено, если вместо параллелограммов сил построить многоугольник сил, то есть, промежуточные векторы при построении равнодействующих и можно не строить, а последовательно, в указанном выше порядке (соответствует формуле 3), одну за другой отложить все указанные силы и начало первой силы соединить с концом последней слагаемой силы.