Гидравлические машины

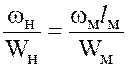и ,

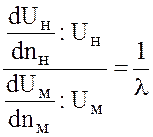будем иметь

,

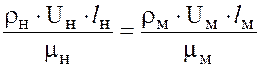где 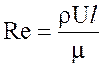— критерий Рейнольдса.

Таким образом, подобие сил трения в потоках, удовлетворяющих условиям геометрического, кинематического и материального подобия, будет только в том случае, если для каждой пары соответственных точек потока натуры и модели число Рейнольдса будет иметь одно и то же значение. В числе Рейнольдса за величину U может быть принята средняя скорость потока V, а за l — любая характерная линейная величина. Например, при изучении законов движения жидкости в трубах применяется диаметр трубы d или гидравлический радиус R. При этом число Рейнольдса будет представлено в виде

; .

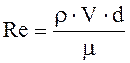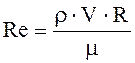Следует иметь в виду, что для подобия двух явлений существенно не численное значение критерия, а лишь его равенство для потоков натуры и модели.

Подставив в выражение (8.1) силу тяжести G = mg, получим

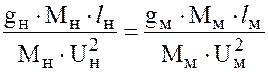
или после сокращения

,

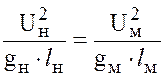где 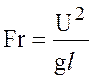— критерий (число) Фруда.

Иногда число Фруда выражают через среднюю скорость:

.

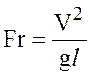Равенство числа Фруда (Fr) в соответствующих точках потоков, удовлетворяющих геометрическому, кинематическому и материальному подобию, обеспечивает подобие сил тяжести. За величину l может быть принята любая характерная линейная величина.

Подставив в выражение (8.1) силу давления Р = р, получим

.

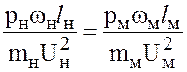Имея в виду, что 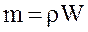и, кроме того, в геометрически подобных системах 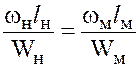, найдем

,

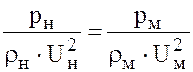где 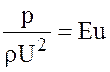— критерий (число) Эйлера.

Числу Эйлера придают несколько иной вид, введя вместо абсолютного давления р разность давления Δр:

.

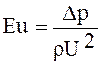Число Эйлера играет большую роль в исследовании явлений, связанных с кавитацией. В этом случае за Δp принимается Δp = p — рп, где рп – давление парообразования. Число k=2Еu называется числом кавитации. Таким образом, равенство чисел Эйлера обеспечивает в динамически подобных потоках подобие сил давления.

В некоторых гидравлических исследованиях существенное значение имеет поверхностное натяжение. Для получения соответствующих условий подобия можно также исходить из критерия Ньютона, подставляя в него значение силы поверхностного натяжения F=, где σ — коэффициент поверхностного натяжения. Преобразования, не отличающиеся от предыдущих, позволяют получить число Вебера – критерий подобия сил поверхностного натяжения в виде

,

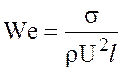где l — характерная линейная величина.

Раздел 2

Гидравлические машины

гидравлические машины делятся на два класса: насосы и гидродвигатели.

9. Насосы

Насос – это гидравлическая машина, которая служит для преобразования механической энергии двигателя в энергию перемещаемой жидкости.

насосы являются одной из самых распространенных разновидностей машин. Их используют для различных целей: подачи воды для водоснабжения и орошения, отвода ее с осушительных систем, для работы гидравлического транспорта и систем теплоснабжения. Это силовая часть гидравлических приводов. Системы смазки и охлаждения двигателей внутреннего сгорания немыслимы без насосов.

Конструктивное разнообразие насосов чрезвычайно велико.

9.1. Классификация насосов

Классификация насосов согласно государственному стандарту дана с точки зрения принципа их действия. При этом прослеживаются и конструктивные признаки (рис. 9.1).

Рис. 9.1

9.2. Основные параметры насосов

Основными выходными параметрами насосов, характеризующими их работу как гидравлической машины, являются подача Q, м3/с, л/с, л/мин; напор (давление) Н(р), м в. ст (Па); мощность N, кВт и коэффициент полезного действия η.

Параметр «напор» характерен для насосов динамических, «давление» — для объемных.

9.2.1. Напор, развиваемый насосом

Необходимость в определении напора возникает в двух случаях: при эксплуатации насосной установки; при проектировании насосной установки.

Напор, развиваемый насосом, есть разность удельных энергий на выходе и входе насоса: Н = Евых-Евх (рис.9.2).

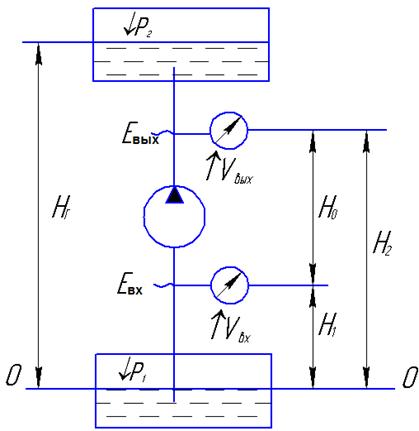
Рис.9.2

Согласно уравнению Бернулли для выходного и входного сечений, где установлены приборы для измерения давлений, относительно плоскости сравнения О-О эти энергии можно определить по выражениям

;

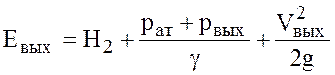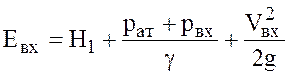(pвх>рат).

Тогда

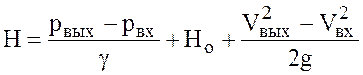. (9.1)

Если рвх<рат, т. е. на входе в насос установлен вакуумметр, то 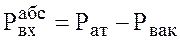. тогда

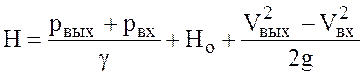. (9.2)

По выражениям (9.1) и (9.2) определяется напор при эксплуатации насосной установки.

При проектировании насосной установки напор насоса определяется из выражения

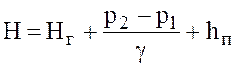, (9.3)

где Нг – геометрическая высота подъема; р1, р2 – давление на свободных поверхностях; hп – гидравлические потери.

9.2.2. Мощность и КПД насоса

Так как насос является преобразователем механической энергии в гидравлическую (рис. 9.3), то такое преобразование всегда связано с потерей энергии. К насосу подводится мощность N, а после насоса отводится полезная Nп в виде гидравлической, т. е. Nп<N (рис. 9.4). Такое неравенство оценивается коэффициентом полезного действия насоса η, т. е. ;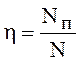

Nп=QH=рQ.