Метод юнга

2.2. Некоторые методы наблюдения интерференции света

2.2.1. Метод Юнга. Источником света слу­жит ярко освещенная щель S, от которой световая волна падает на две узкие равноудаленные щели S1 и S2, па­раллельные щели S. Таким образом, щели S1 и S2, играют роль ко­герентных источни­ков. Интерференционная картина (об­ласть R2Q1) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S1 и S2 (рис. 2–1а).

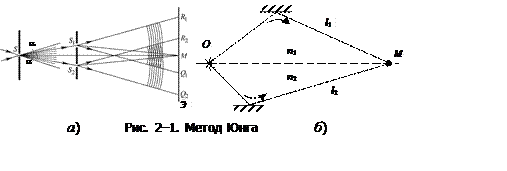Проведем расчет интерференционной картины (рис. 2–1,б). Пусть разделение на две когерентные волны происходит в некоторой точке О. До точки М, где наблюдается интерференционная картина, одна волна прошла путь l1 в среде с показателем преломления n1, вторая волна – путь l2 в среде с показателем преломления n2. Если в начальный момент времени фаза колебаний равна wt, то в точке М первая волна возбудит колеба­ние 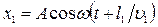, а вторая — колебание 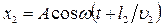, где u1=с/n1 и u2=с/n2 — соответственно фазо­вая скорость первой и второй волны. Под х будем понимать на­пряженность электрического (световой вектор) или маг­нитного полей волны; векторы и ко­леблются во взаимно перпендикулярных плоскостях.

Разность фаз колебаний d=j2–j1, возбуждаемых волнами в точке М, равна

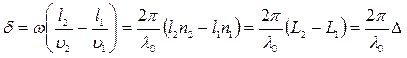. (2.1)

В соотношении (2.1) мы учли, что ,

где l0 –длина волны в вакууме.

Произ­ведение геометрической длины пути световой во­лны l в данной среде на показатель пре­ломления n этой среды называется оптиче­ской длиной пути, a — раз­ность оптических длин проходимых во­лнами путей — называется оптической разностью хода.

Если оптическая разность хода равна четному числу полуволн в вакууме (целому числу волн)

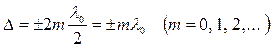, (2.2)

то 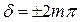и колебания, возбуждаемые в точке М обеими волнами, про­исходят в одинаковой фазе и будет наблюдаться интерферен­ционный максимум.

Если оптическая разность хода равна нечетному числу полуволн в вакууме

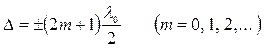, (2.3)

то и колебания, возбуждаемые в точке М обеими волнами, бу­дут про­исходить в противофазе и будет наблюдаться интерферен­ционный минимум.

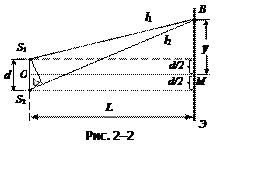Пусть среда, в которой распространяется свет, однородная, а интерференция наблюдается в произвольной точке В экрана, параллельного щелям и расположенного от них на расстоя­нии L, причем . Показатель пре­лом-ления среды n = 1 (Рис. 2-2).

Интенсивность в точке В определяется оптической разностью хода . Из рисунка следует, что ,

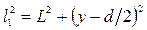, откуда .

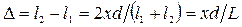Согласно условию 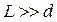, поэтому 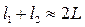и .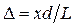

Подставив это значение в условия максимума и минимума (2.2 и 2.3), получим координаты — где интенсивность света максимальна и — где интенсивность света минимальна:

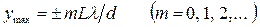, (2-4)

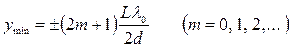. (2-5)

Ширина интерференционной полосы — расстояние между двумя сосед­ними максимумами (или минимумами)

.

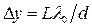Согласно (2-4) и (2-5), интерференционная картина представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m = 0, проходит через точку М. Вверх и вниз от него на равных расстояниях друг от друга располагаются соответственно максимумы (минимумы) первого (m = 1), второго (m = 2) порядков и т. д. Описанная картина справедлива только при освещении монохроматическим светом. В случае белого света интерференционная картина будет иметь вид радужных полос.

2.2.2. Зеркала Френеля. Свет от источника S (рис. 2–3) падает расходящимся пучком на два плоских зеркала МО и NO, распо­ложенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол a мал).

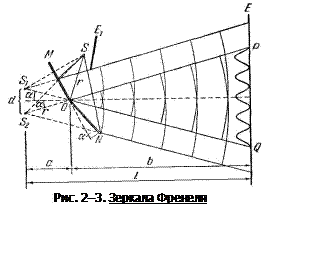
Применяя правила по­строения изображения в плоских зерка­лах, можно показать, что и источник, и его изображения S1 и S2 (угловое расстояние между которыми равно 2a) лежат на од­ной и той же окружности радиуса r с цент­ром в O (точка соприкосновения зеркал), т. е. ОS = ОS1 = ОS2 = r.

Световые пучки, отразившиеся от обо­их зеркал, можно считать выходя­щими из источников S1 и S2, которые являются мнимыми изображениями S в зеркалах. Источники S1 и S2 коге­рентны, и исходящие из них световые пуч­ки, встречаясь друг с другом, интерфери­руют в области взаимного перекрытия. Интерфе­ренционная картина наблюдается на экра­не (E) в области PQ. Для исключения попадания на экран пря­мых лучей света от источника S используется заслонка (E1).

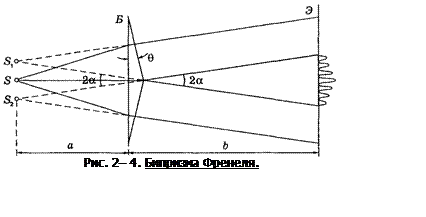
2.2.3. Бипризма Френеля. Бипризма состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S (рис. 2–4) преломля­ется в обеих призмах, в результате чего за биприз­мой распространяются световые лу­чи, как бы исходящие из мнимых ис­точников S1 и S2, являющихся когерентными.

На поверх­ности экрана (в области PQ) про­исходит наложение когерентных пучков и наблюдается интерференция.

2.2.4. Интерференция света в тонких пленках. Пусть на плоскопараллельную про­зрачную пленку с показателем преломле­ния n и толщиной h под углом a падает плоская монохроматическая волна (для простоты рас­смотрим только один луч из падающего пучка – 1). На поверхности пленки в точке A луч 1 де­лится на два: частично отразится от верх­ней поверхности пленки, а частично пре­ломится (рис. 2–4). Пленка находится в воздухе (абсолютный показа­тель преломления n0=1).

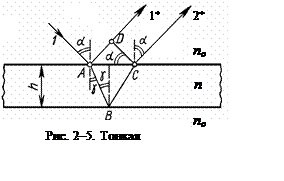Преломленный луч в точ­ке B частично преломится, а частично отразится и пойдет к точке С. Здесь он опять частично отразится и преломится, выходя в воздух под углом a (луч 2*). Если оптическая разность хода этих лучей будет мала по сравнению с длиной когерентности па­дающей волны, то эти лучи будут когерент­ными. Если на их пути поставить собирающую линзу то они сойдутся в одной из точек фокальной плоскости линзы и дадут интерференционную кар­тину, которая будет определяться оптиче­ской разностью хода между интерферирующи­ми лучами. Интерференци­онные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона.