Гидродинамика

Применение гидроаккумуляторов дает возможность ограничивать мощность насосов величиной средней мощности потребителей гидравлической энергии или же, в системах с эпизодическим действием, обеспечить перерывы в работе насосов.

Особое преимущество аккумуляторы имеют в гидросистемах с эпизодическими большими пиками расхода, которые в некоторых случаях во много раз превышают средний расход жидкости в системе. энергия, накопленная в аккумуляторе, может быть отдана в очень короткое время, поэтому аккумулятор может кратковременно развить большую мощность.

Аккумуляторы применяют также в машинах, в которых необходимо обеспечить компенсацию утечек при длительной выдержке изделия под давлением. К подобным случаям относятся формовка и вулканизация изделий из каучука, прессование деталей из пластмасс и пр.

Кроме того, аккумулятор служит аварийным источником энергии, компенсатором утечек, гасителем гидравлических ударов.

В практике машиностроения применяют в основном газовые (пневматические), грузовые и пружинные аккумуляторы (рис.3.22).

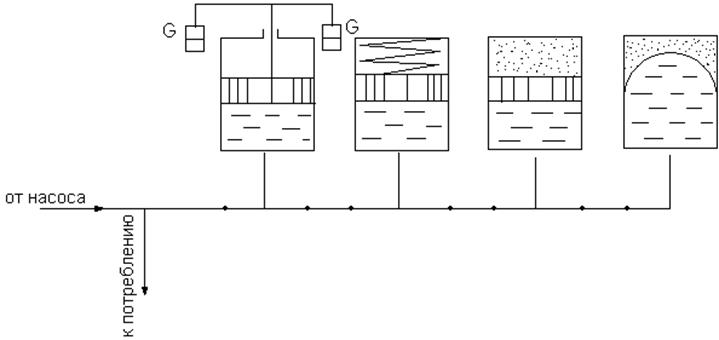
Рис.3.22

Максимальное давление, которое получают в машиностроении с помощью насосов, обычно не превышает 700 ат. Для получения более высоких давлений обычно применяют повысители давления (мультипликаторы), что особенно целесообразно в тех случаях, когда необходимо развить большие давления при малых расходах жидкости.

В прессах распространены мультипликаторы, повышающие давление насоса от 210…350 до 1100 ат. К. п.д. подобных мультипликаторов находится в пределах 0,94…0,96.

Коэффициент усиления мультипликатором, под которым понимают отношение выходного давления к входному, находится в пределах 1000:1. Так, например, существуют парогидравлические мультипликаторы, которые повышают давление от 7 до 6000 ат.

Наиболее распространенная схема мультипликатора представлена на рис.3.23.

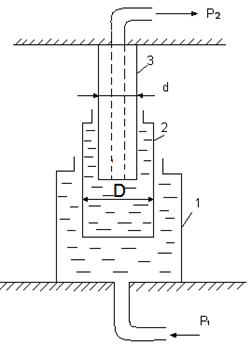
Рис.3.23

Давление p1 подводится в цилиндр 1, внутрь которого входит подвижный полый цилиндр 2 весом G и диаметром D. Цилиндр скользит по неподвижному плунжеру 3 диаметром d, канал которого отводит жидкость под повышенным давлением p2.

4. Гидродинамика

4.1. Основные понятия

Гидродинамика – раздел гидравлики, который изучает законы движения жидкости.

Представим себе движущуюся сплошную среду, каковой является жидкость, например, в лотке переменного в плане сечения. Поместим на поверхности множество миниатюрных корабликов со светящимися лампочками. Сфотографировав в темноте с определенной выдержкой на пленке, мы получим штрихи, длина которых будет различна, т. е. светящиеся точки движутся с различными скоростями в различных направлениях (рис.4.1).

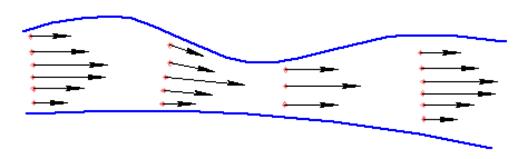
Рис.4.1

Мгновенная картина скоростей частиц жидкости в пространстве, заполненном жидкостью, называется полем скоростей.

Если бы нам удалось определить в точках движущейся жидкости давление, то мгновенная картина давлений называлась бы полем давлений.

Движущаяся жидкость может иметь два принципиально различных поля: скоростей и давлений.

Если поле скоростей и давлений не зависит от времени, то движение называется установившимся, или стационарным. Примером такого движения может быть течение жидкости из резервуара с постоянным уровнем по трубопроводу постоянного или переменного диаметра (рис.4.2).

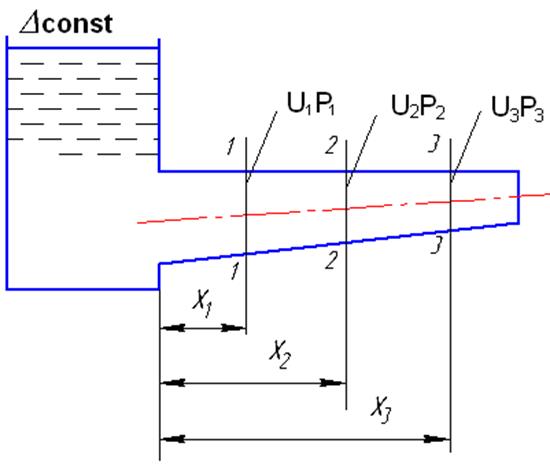
Рис.4.2

В сечениях 1-1, 2-2, 3-3 и т. д. скорости и давления будут разными, но во времени они останутся постоянными, т. е. поля скоростей и давлений являются функцией только координат U, р =f(x, y,z).

Если поле скоростей и давлений зависит от времени, то движение называется неустановившимся, или нестационарным. Примером такого движения может служить опорожнение резервуара по трубопроводу, моменты включения или выключения насосов, закрытие или открытие запорной арматуры и т. п. В этом случае U, р =f(x, у,z, t).

Аналитическое изучение в целом движущейся сплошной среды является сложной задачей. Для понимания физической сущности явлений, происходящих в движущейся жидкости, и возможности их математического описания в классической гидромеханике вводят струйную модель движения жидкости.

Представим себе, что в точках 1,2,3,4,5 и т. д., находящихся на бесконечно малом расстоянии друг от друга, движущейся жидкости нам известны векторы скоростей . Линию, проведенную касательно к этим векторам, будем называть линией тока (рис.4.3). В установившемся движении она совпадает с траекторией, в неустановившемся – не совпадает.

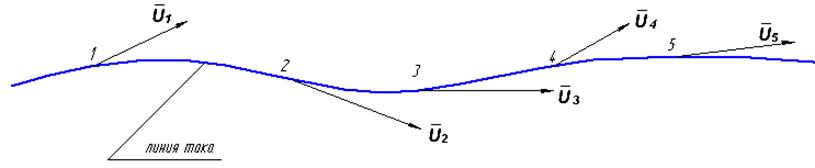
Рис.4.3

Теперь движущуюся сплошную среду представим состоящей из бесконечно большого числа линий тока (рис.4.4).

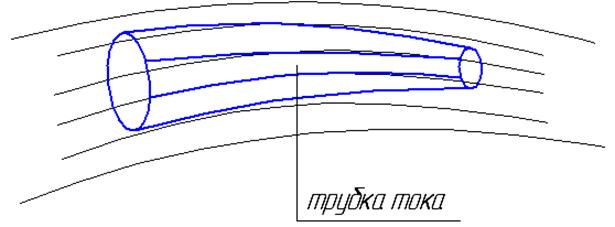
Рис.4.4

Выделим в сплошной среде на каком-то расстоянии друг от друга два замкнутых контура и через их периметры проведем лини тока (рис.4.4). Образуется трубка тока, а жидкость, протекающую внутри этой трубки тока, будем называть элементарной струйкой, а их совокупность – потоком.

Сечение, нормальное в каждой своей точке к линиям тока, называется живым сечением струйки. Площадь живого сечения обозначим через d. Ввиду малости живого сечения элементарной струйки местные скорости жидкости в его пределах можно считать одинаковыми.

В общем случае скорость и площадь живых сечений по длине струйки могут изменяться. Будет считать, что обмен жидкостью между струйками отсутствует.

Количество жидкости, протекающее через живое сечение струйки в единицу времени, называется элементарным расходом. Он бывает объемный, массовый и весовой:

объемный расход dQ = U d, м3/с;

массовый расход dМ = 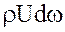, кг/с;

весовой расход dG = 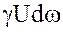, Н/с.

Для потока живое сечение будем считать условно плоским и проведенным нормально к его оси.

Так как по живому сечению потока скорости струек распределяются неравномерно, то для определения объемного расхода необходимо знать закон распределения этих скоростей, что является довольно сложной задачей. Для упрощения определения расхода потока введено понятие средней скорости потока V. Это такая воображаемая скорость, с которой должны двигаться все частицы потока, чтобы расход оказался равным расходу при движении жидкости с действительными неодинаковыми для отдельных частиц скоростями. Единственный способ определения средней скорости: является 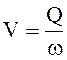. таким образом, для потока:

объемный расход Q = ;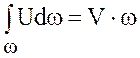

массовый расход М = ;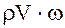

весовой расход G = .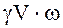

В зависимости от причин и общих условий, при которых происходит движение, различают безнапорное и напорное движения.

Безнапорное движение – это движение жидкости под действием сил тяжести и при наличии свободной поверхности (каналы, реки, канализационные системы) (рис.4.5). В этом случае обеспечивается геометрический уклон .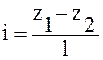

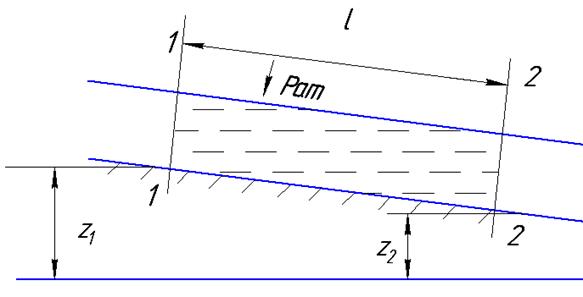
Рис.4.5

Напорное движение жидкости в потоке – это, как правило, движение без свободной поверхности. Условием такого движения должна быть разность давлений по длине потока: р1>р2 (рис.4.6).

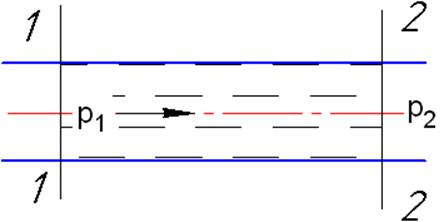
Рис.4.6

разнообразие геометрических форм живых сечений потока и необходимость универсализации расчетных зависимостей обусловили введение понятия гидравлический радиус, который равен отношению площади живого сечения к длине смоченного периметра в этом сечении: 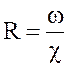. Так, например, для живого сечения круглой формы радиусом гидравлический радиус 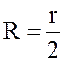.