Гидродинамика и биофизика кровообращения

Основные законы гидродинамики

Гидродинамика — раздел физики, изучающий движение жидкостей. Реология – область физики, которая изучает деформационные свойства и текучесть вещества.

Биофизика кровообращения основывается на законах гидродинамики и реологии

Уравнение неразрывности струи

Чтобы описать движение жидкости, можно отметить любые точки пространства и определить скорость (линейную скорость), с которой отдельные частицы жидкости проходят через каждую точку. Если вектор скорости в каждой точке остается постоянным, то течение жидкости называется стационарным. Линии в движущейся жидкости, проведенные так, чтобы касательная к ним совпадала по направлению с вектором скорости, называются линиями тока. Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Выделим трубку тока, настолько узкую, чтобы скорость v в ее сечении S, перпендикулярном к оси трубки, была одинаковой по всему данному сечению (рис.4). Объем жидкости V, протекающий через каждое сечение за единицу времени t, называется объемной скоростью Q (не смешивать со скоростью):

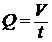
Рис. 4. Трубка тока

Очевидно, что объемная скорость Q пропорциональна скорости течения жидкости ( линейной скорости) и площади поперечного сечения S:

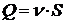
Как известно, жидкость является практически несжимаемой. Если жидкость течет неразрывной струей, то величина Q в любом сечении трубки должна быть одинаковой: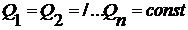

Отсюда следует: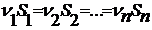

Это выражение представляет уравнение неразрывности струи. Смысл его заключается в том, что произведение скорости течения жидкости на площадь поперечно сечения трубки во всех сечениях одинаково.

Из этого уравнения следует, что скорость течения жидкости в любом сечении трубки обратно пропорциональна площади этого сечения:

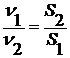
В более широком сечении трубки скорость жидкости уменьшается, а в более узком увеличивается.

Данное уравнение выведено для трубки тока настолько узкой, что скорость течения жидкости во всех точках ее поперечного сечения можно считать одинаковой. Как будет показано ниже, в реальных трубках, достаточно широких скорость жидкости в разных точках сечения различна. Однако, если пользоваться величиной средней скорости, уравнение неразрывности струи сохраняет значение и в этих условиях.

Давление жидкости в трубках

Давлением Р называется сила F, приходящаяся на единицу площади поверхности S, на которую действует эта сила, и направленная перпендикулярно к данной поверхности:

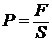
Полное давление Рполн в движущейся жидкости, соответствует ее удельной энергии, то есть энергии, приходящейся на единицу объема. За счет этой энергии жидкость может совершать работу. Величина полного давления в любом сечении трубки, по которой течет жидкость, описывается уравнением, в которое входят три слагаемых:

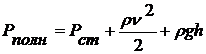
В этом уравнении Рст — статическое давление, обусловленное силами

упругости жидкости. — динамическое давление, которое зависит от скорости течения жидкости и ее плотности , — гидростатическое (гидравлическое)

давление, которое определяется плотностью жидкости и высотой h данного сечения трубки над условно выбранным уровнем.

Если жидкость течет по горизонтальной трубке, ее полное давление описывается более простым выражением: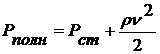

Допустим, жидкость течет по горизонтальной трубке в направлении, указанном стрелкой (рис.5). Тогда о величине статического давления можно судить по высоте подъема жидкости в манометрической трубке 1, а о величине полного давления — в манометрической трубке 2. Разница между уровнями жидкости в этих трубках соответствует динамическому давлению.

Рст соответствует удельной потенциальной энергии жидкости, а — ее удельной кинетической энергии.

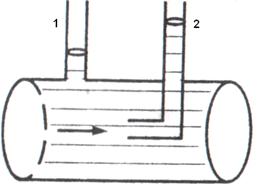
Рис.5. Измерение статического и динамического давления

в движущейся жидкости.

Если бы жидкость была лишена трения ("идеальная жидкость"), ее энергия

не расходовалась бы на его преодоление, величина полного давления в любом сечении трубки оставалась бы постоянной.

Но реальная жидкость обладает внутренним трением, значение которого описано ниже. На его преодоление расходуется энергия жидкости, и поэтому величина полного давления снижается на протяжении трубки, по которой она течет. При этом динамическое давление на отдельных участках трубки может уменьшаться, либо даже увеличиваться (за счет снижения статического давления). Но их сумма (полное давление жидкости) не может ни оставаться неизменным, ни, тем более, увеличиваться по ходу трубки, а только снижаться, что вытекает из закона сохранения энергии.

Вязкость и внутреннее трение жидкости

Внутреннее трение жидкости обусловлено силами взаимодействия между ее молекулами. Проблему вязкости жидкости впервые исследовал Ньютон, который отметил "недостаточное скольжение" между ее частицами. В дальнейшем вместо этого выражения стали употреблять термин "вязкость".

Вязкость определяет реологические свойства жидкости. Эти свойства легче всего проследить на примере течения жидкости между параллельными пластинами, расстояние между которыми равно х (рис.6).

Пусть нижняя пластина закреплена, а верхняя движется с постоянной скоростью. Жидкость, находящаяся между пластинами и обладающая вязкостью, оказывает сопротивление этому «сдвигу». Поэтому необходимо, чтобы на верхнюю пластину действовала постоянная сила F.

При перемещении верхней пластины жидкость приходит в движение. Она движется так, что между пластинами создается определенное распределение скоростей. С наибольшей скоростью перемещается слой, прилегающий к верхней пластине. Он увлекает за собой следующий слой, но с меньшей скоростью и т. д. В результате между пластинами возникает градиент скорости течения жидкости 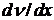. Слой, который прилегает к нижней пластине, остается неподвижным.

Рис.6. Распределение величины скорости в слое жидкости при ее течении.

Сила, действующая, на верхнюю пластину, необходима для преодоления трения жидкости. Она равна по своей величине силе трения и описывается уравнением Ньютона:

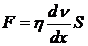
В этом уравнении 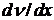— градиент скорости, который описывает изменение скорости в направлении, перпендикулярном ее вектору. S — площадь поверхности пластин, т. е. площадь взаимодействующих слоев жидкости, ("эта") — коэффициент пропорциональности, который называется коэффициентом вязкости, или просто вязкостью. Он численно равен силе, которую нужно приложить к подвижной пластине, если площадь ее равна единице, при градиенте скорости, также равном единице.