Гипотеза ньютона

гипотеза Ньютона стала законом жидкостного трения. В математической форме он выражается следующим образом

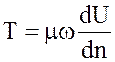, (2.11)

где Т – сила внутреннего трения, н; – градиент скорости, имеющий положительный или отрицательный знак в зависимости от характера изменения скорости по сечению; dU – разность скоростей движения соседних соприкасающихся слоев жидкости в предположении, что эти слои являются бесконечно тонкими, м/с; dn – расстояние между осями соседних слоев, м; ω – площадь соприкасающихся слоев, м2; μ — динамический коэффициент вязкости, Па·с.

Силу трения Т, отнесенную к единице площади ω, называют касательным напряжением:

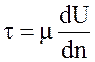. (2.12)

Жидкости, подчиняющиеся выражениям (2.11) и (2.12), принято называть ньютоновскими.

Наряду с динамической вязкостью μ в гидравлических расчетах применяют кинематическую вязкость:

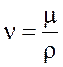,м2/с (2.13)

Единицей измерения кинематической вязкости является стокс 1 Ст = 1 см2/с. Сотая часть стокса называется сантистоксом (сСт). Приборы для измерения вязкости называются вискозиметрами.

Динамическую вязкость можно определить ротационными вискозиметрами.

На практике часто сравнивают время истечения жидкости со временем истечения воды. Это отношение называют условной вязкостью (ВУ) и измеряют в градусах Энглера:

º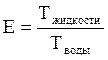. (2.14)

Но величина условной вязкости безразмерна и при решении задач неудобна, поэтому существуют эмпирические формулы пересчета. Одна из них

ºЕ — 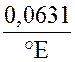, см2/с (2.15)

В США и Англии получили распространение единицы измерения вязкости в секундах Редвуда (´´Re) и Сейболта (´´S), во Франции – градусы Барбье (оВ).

Вязкость жидкостей существенным образом зависит от температуры. Она уменьшается с ее ростом. От увеличения давления вязкость также зависит, увеличиваясь с его ростом. Причем эта зависимость для разных температур будет различной.

В пределах относительно небольших давлений (0…40 МПа) вязкость, например, минеральных масел изменяется с изменением давления практически линейно (примерно в три раза). В пределах давления 0…150 МПа вязкость повышается в 17 раз, 0…400 МПа – в сотни раз. При давлениях порядка 150…2000 МПа минеральные масла затвердевают.

Кроме ньютоновских жидкостей, существуют жидкости аномальные (структурные), которые не подчиняются закону Ньютона, и поэтому их называют неньютоновскими. Это осадки сточных вод (гели), цементные, глинистые и меловые растворы, парафинистые нефти вблизи температуры их застывания, разнообразные коллоидные растворы (белок, крахмал, клей), нефтяные эмульсии (смеси с водой), суспензии (шламы, гидроторф, озерный ил, битумы), молочные продукты, кормовые смеси, различного рода пасты.

Перечисленные аномальные жидкости подчиняются закону Шведова – Бингама

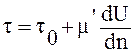, Н/м2 (2.16)

где — начальное напряжение сдвига; µ′ — структурная вязкость.

Жидкости, подчиняющиеся выражению (2.16), называются еще бингамовскими, или вязко-пластичными. Для повышения достоверности расчетов таких жидкостей начальное напряжение сдвига , как правило, определяют экспериментально.

3. Гидростатика

В гидростатике рассматривается жидкость, находящаяся в общем случае в состоянии относительного покоя, т. е. при отсутствии взаимного перемещения отдельных ее частиц. При этом жидкость перемещается как твердое тело.

Частным случаем относительного покоя является «абсолютный» покой, под которым подразумевается покой относительно земли. Приведем несколько примеров.

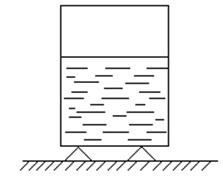
1. Абсолютный покой – жидкость находится в покое в резервуаре, неподвижном относительно земли (рис. 3.1).

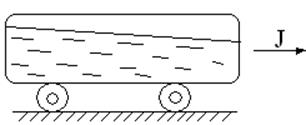
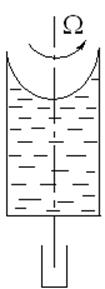
2. Относительный покой: а) жидкость находится в покое относительно железнодорожной цистерны, которая вместе с жидкостью движется прямолинейно с некоторым ускорением J (рис.3.2); б) жидкость находится в покое относительно резервуара, который вместе с жидкостью вращается с постоянной угловой скоростью W (рис.3.3).

На жидкость, находящуюся в относительном покое, действуют массовые силы (сила тяжести и сила инерции переносного движения), а из поверхностных сил — только силы давления.

3.1. Свойства гидростатического давления

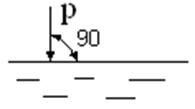
Гидростатическое давление направлено всегда по внутренней нормали к площадке, на которую оно действует (рис.3.4).

Доказательство ведется от обратного утверждения.

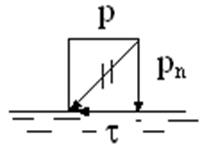
Допустим, гидростатическое давление направлено не по нормали к площадке (рис.3.5). В этом случае его можно разложить на нормальную рn и касательную составляющие t. Появление касательной составляющей станет нарушением условия относительного покоя, т. е. частицы жидкости якобы будут перемещаться друг относительно друга.

Допустим, гидростатическое давление направлено по внешней нормали к площадке (рис.3.6). Это значило бы, что жидкость сопротивляется растягивающим усилиями, что нарушило бы принятую ранее аксиому.

Гидростатическое давление в любой точке покоящейся жидкости не зависит от направления площадки, для которой оно вычислено.

Проиллюстрируем это свойство. В жидкости на глубине h мысленно возьмем точку А (рис.3.7). Можно предположить, что давление в этой точке

будет совершенно одинаковым для направления площадок 1-1, 2-2, 3-3 и т. д., проходящих через эту точку. Докажем это очевидное свойство.

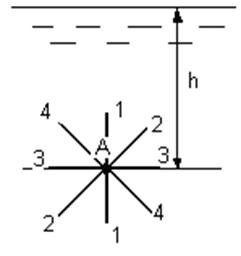
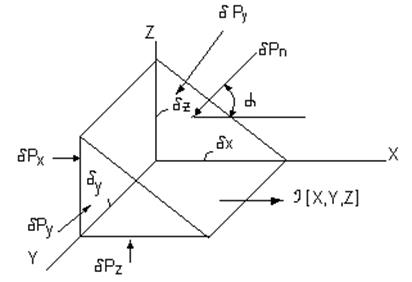
Рис. 3.7 Рис. 3.8

Для этого в жидкости, находящейся в покое, разместим оси координат и выделим в этих осях элементарный объем в виде прямоугольного клина (рис.3.8), стороны граней которого по осям равны δх, δу, δz. Применим принцип отвердевания, т. е. мысленно представим, что бесконечно малый объем превратился в твердое тело. В этом случае при рассмотрении тела в покое можно применить законы механики твердого тела, т. е. если тело находится в равновесии (покое), то сумма проекций всех сил на соответствующие оси равна нулю, т. е. ΣPx = 0, ΣPy = 0, ΣPz = 0.

На выделенный объем действуют массовая сила, вызванная ускорением J, проекции которого на соответствующие оси будут равны X, Y, Z, и поверхностные силы на соответствующие грани δPх, δPу, δPz, δPп. Направление грани с индексом «n» в системе координат взято произвольно.

Составим уравнение проекции сил на ось Х:

ΣРх = δРх — δРп·cosα + ХδМ = 0. (3.1)

Ввиду малости размеров граней клина будем считать, что давление на каждую из них будет одинаковым и каким-то средним, тогда

.

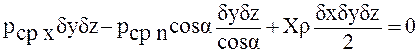Сократив на δу·δz, получим:

.
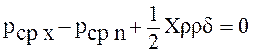