Неавтономные системы, параметрический генератор
|
|
(1.20) |
и в емкостной трёхточке:
|
|
(1.21) |
Также рассмотрим мост Вина (рис. 15), который используется для генерации в области звуковых частот.
|
Рис. 13. Индуктивная трёхточка. |
Рис. 14. Емкостная трёхточка. |
Операторное сопротивление такого генератора равно
|
|
(1.22) |
Рис. 15. Мост Вина. |
|
Опять подставляя уравнение для операторного сопротивления в (1.16), получим ДУ этого контура: |
||
|
|
(1.23) |
|
|
Все рассмотренные генераторы являются активными, нелинейными, автономными системами. |
||
1.4. Неавтономные системы, параметрический генератор
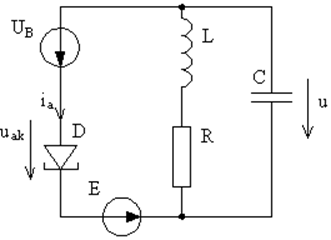
В пункте 1.1. вводилось определение неавтономных систем, и отмечались способы воздействия на неавтономную систему. Рассмотрим на конкретных примерах силовое и параметрическое воздействия. Начнём с силового воздействия: для этого вернёмся к генератору на туннельном диоде с дополнительным источником напряжения (рис. 16), который и играет роль внешнего воздействия.
Уравнение, описывающее колебательные процессы в этом генераторе, от (1.13) будет отличаться тем, что добавится внешнее воздействие:
|
|
(1.24) |
|
Рис. 16. Генератор на туннельном диоде. |
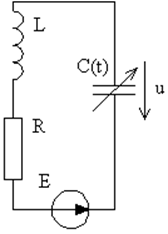
Рис. 17. Колебательный контур. |
Перейдём к параметрическому воздействию и рассмотрим контур, изображённый на рис. 17. При определённой частоте внешнего воздействия (при резонансе) возможна потеря устойчивости и возникновение колебаний с частотой кратной частоте внешнего воздействия. Опишем эту систему. В качестве обобщённых координат возьмём заряд. Для простоты также пусть Е = 0, тогда, так как u = q/C(t), уравнение колебательного контура запишется в виде:
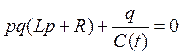 .
.
В частном случае (если в качестве переменной ёмкости — варикап), т. е. справедлива следующая зависимость
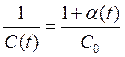 ,
,
символическое уравнение системы принимает вид:
|
|
(1.25) |
Если a(t) меняется по гармоническому закону, то получится уравнение Матье, а при произвольном изменении — уравнение Хилла.
1.5. Уравнение Лагранжа для колебательных систем Вопрос 3
Уравнение движения Лагранжа удобно тем, что уравнение движения записывается в ковариантной форме, т. е. структура уравнения не меняется при переходе к другим координатам.
Любая механическая система описывается уравнением Ньютона:
|
|
(1.26) |
и это самая общая форма записи (форма Коши). Известно, что, если заданы начальные условия
![]() и
и ![]() ,
,
то решение существует и единственно.
В общем случае на уравнение накладываются связи, уменьшая количество независимых координат:
|
|
(1.27) |
Если у нас есть k связей, то только n = m — k координат являются обобщёнными. Выбираем обобщённые координаты q1, …, qn так, чтобы их связь с первичными была точечной:
|
|
(1.28) |
Допустим, что силы, действующие на систему, являются потенциальными, т. е. существует функция 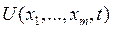 такая, что для каждой силы выполняется равенство
такая, что для каждой силы выполняется равенство
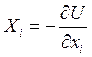 , где
, где 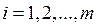 .
.
В этом случае для описания движения в потенциальном поле можно воспользоваться формализмом Лагранжа:
1. Выбираем обобщённые координаты q1, …, qn.
2. С помощью уравнения преобразования координат (1.28) записываем выражение для энергии через эти координаты:
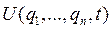 .
.
3. С учётом преобразования обобщённых скоростей
|
|
(1.29) |
строим выражение для кинетической энергии системы![]() .
.
4. Составляем лагранжиан системы ![]() .
.
5. Записываем уравнение движения системы в виде:
|
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
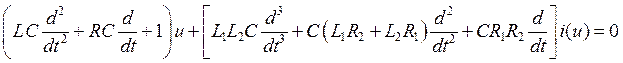 ,
,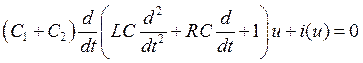 .
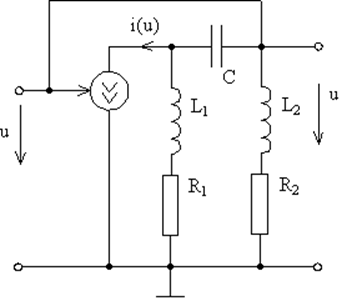
.
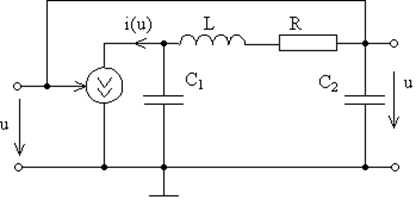
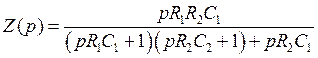 .
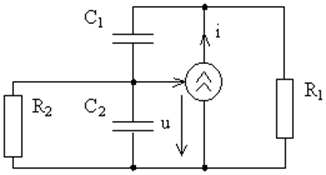
.
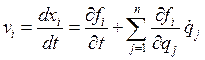
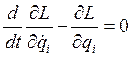 , где
, где 

