Главные направления и главные деформации

Но с другой стороны

.

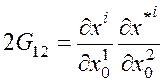Поэтому

,

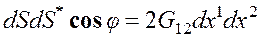а с учетом полученных ранее соотношений

получается формула для изменения угла

.

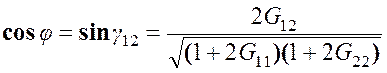Аналогично получаются соответствующие выражения для остальных углов.

Если ограничиться малыми деформациями, то геометрический смысл компонент деформаций приобретает ясный смысл: компоненты деформаций с одинаковыми индексами равны относительным удлинениям бесконечно малых отрезков, взятых в направлении соответствующих координатных линий; компоненты деформаций с разными индексами равны углам скашивания первоначально прямых углов между бесконечно малыми отрезками, взятых вдоль направления соответствующих координатных линий.

Другими словами, компоненты деформации с одинаковыми индексами описывают относительные удлинения среды, а компоненты деформации с разными индексами описывают сдвиги, первоначально ортогональных элементов

2.4 ГЛАВНЫЕ НАПРАВЛЕНИЯ И ГЛАВНЫЕ ДЕФОРМАЦИИ

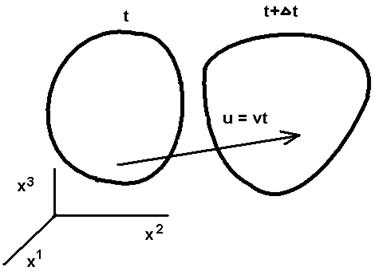
При повороте выбранной системы координат компоненты тензора деформаций преобразуются по соответствующим формулам перехода. Известно, что для каждого тензора второго ранга существуют три инварианта, не зависящие от ориентации системы координат:

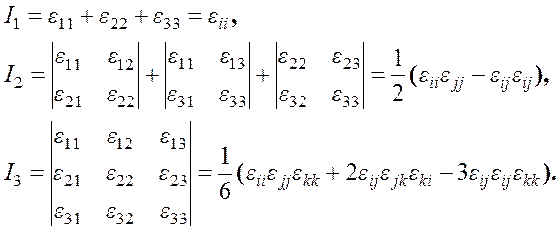
Для тензора деформаций возникает задача определения для данной точки области тех направлений, в которых тензор малых деформаций имеет только относительные удлинения элементов и не имеет сдвигов. Если преобразовать компоненты тензора деформаций к таким осям, то для этих направлений тензор деформации будет шаровым. Отсюда получаем, что если такие направления существуют, то должны выполняться условия коллинеарности векторов и , т. е. должны выполняться равенства ( — коэффициент пропорциональности)

.

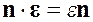В силу симметрии тензора деформации предыдущее равенство можно переписать в компонентах декартовой системы координат

.

Условия разрешимости этих уравнений приводят к характеристическому уравнению для тензора деформаций

с коэффициентами, равными инвариантам тензора деформаций. Использование теоремы Виета позволяет выразить инварианты через корни полученного характеристического уравнения

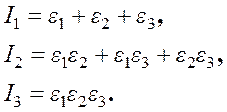
Т. к. собственные значения вещественного симметричного тензора второго ранга являются всегда вещественными числами, то главные деформации всегда вещественны.

2.5 ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИЙ

В жидких и газообразных телах такая характеристика, как деформация не играет почти никакой роли. Действительно, если поменять местами, допустим две частицы в газообразной среде, то изменится конфигурация, и как следствие, появится деформация. Но на внутреннее состояние газа это фактически не скажется. Другое дело, если будем учитывать скорость перемены этих двух частиц, тогда интенсивность такой перемены будет менять внутреннее состояние газа. Чтобы охарактеризовать или оценить в какой-то мере интенсивность изменения деформированного состояния вводится тензор скоростей деформаций. Для этого рассмотрим две бесконечно близкие текущие конфигурации в момент времени и , отличающиеся на момент времени см. рис. 3. Пусть, к тому же, известно поле скоростей в момент времени . Тогда можно определить перемещения частиц за промежуток времени : . Принимая условно конфигурацию в момент времени за «отсчетную», а конфигурацию в момент времени 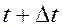за «текущую», и зная поле перемещений, можем найти приращение тензора деформации за этот промежуток времени. Т. к. в «отсчетной» конфигурации исходными являются эйлеровы координат, значки «0» над набла-оператором не пишем, получаем

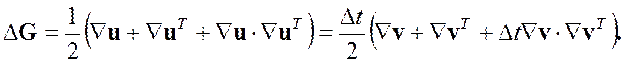
Теперь найдем

(2.4)

Полученный тензор носит название тензора скоростей деформаций.

2.6 ВЕКТОР НАПРЯЖЕНИЙ

Когда не тела действуют внешние нагрузки, они не рассыпаются на отдельные материальные частицы, только потому, что между частицами возникают внутренние силовые взаимодействия. Природа этих взаимодействий лежит в области взаимодействия электрических и магнитных сил. Но для оценки этих взаимодействий на уровне материальных частиц введем новое физическое понятие: вектор напряжений. Рассмотрим некоторое текущее состояние СС, на которую наложены внешние воздействия со стороны окружающих тел. Возьмем внутри объема СС произвольную точку и проведем через эту точку поверхность , делящую весь объем на два объема и , как показано на рис. 4. Выберем на поверхности окрестность точки . Рассмотрим воздействие частиц, находящихся в , на частицы, находящиеся в . Оно осуществляется через малую поверхность и сводится к контактному силовому воздействию. А выражается результирующей силой и результирующим моментом . Направление результирующей силы может не совпадать с направлением нормали . Рассмотрим следующую характеристику, подобно тому, как в гидростатике вводится давление жидкости