Исследование решения двухточечной краевой задачи
1. Задание исследования
Провести исследование решения двухточечной краевой задачи методом прогонки на языке С++.
2. Подробное описание задачи и методы её решения
Физические процессы часто описываются обыкновенными линейными дифференциальными уравнениями второго порядка. В некоторых случаях представляет интерес описание процесса на некотором интервале изменения аргумента при условии, что на обеих границах этого интервала заданы значения линейных комбинаций состояний процесса и его первых производных. Такая задача называется линейной двухточечной краевой задачей и может быть решена с помощью так называемого метода прогонки. Метод прогонки часто еще называют алгоритмом Томаса.
Сначала требуется найти функцию y(x), на отрезке [a, b], которая удовлетворяет следующему дифференциальному уравнению и краевым условиям:
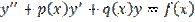
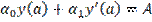
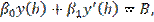
где p(x), q(x), f(x) — известные непрерывные на отрезке [a, b] функции, 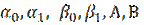 — заданные постоянные, причем
— заданные постоянные, причем 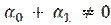 .
.
Предполагается, что отрезок [a, b], на котором будет находиться решение этого уравнения, разбит на n равных частей системой точек (сеткой).
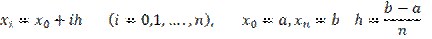
Пусть pi, qi, fi, yi — значения соответствующих функций в узлах сетки. Тогда вычисления производятся в два приема (прямой ход и обратных ход ) следующем порядке:
· Прямой ход:
Вычислить набор значений mi и ki по формулам:
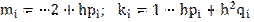 , (i=0,1,…..,n-2)
, (i=0,1,…..,n-2)
Затем находим набор значений ci и di:
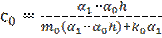 ,
,
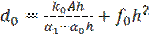 ;
;
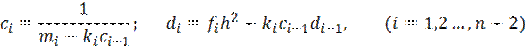
· Обратный ход:
Находим все значения функции yi:
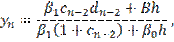
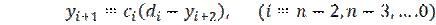
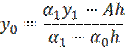
Таким образом, все вычисления как бы прогоняют два раза. Вычисления прямого хода заготавливают вспомогательные числа ci и di в порядке возрастания индекса i. При этом для вычисления с0, d0 используется краевое условие на левом конце отрезка интегрирования. Затем на первом шаге обратного хода происходит согласование полученных чисел сn-2, dn-2 с краевым условием на первом конце отрезка интегрирования, после чего последовательно получаются значения искомой функции yi в порядке убывания индекса i.
Примените метод прогонки для приближенного решения следующей краевой задачи:
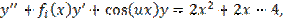
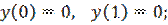
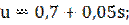
3. Описание работы программы и результаты исследований
Программа написана на языке С и является консольным приложением. Данная программа позволяет получить решение вышеуказанного уравнения на интервале от ab[0;1] в точках Xn с шагом h=(b-a)/n, где n – число точек на интервале, при параметрах fi и S. Значения fi приведены в таблице. S же, изменяется от нуля до пяти, с шагом в единицу.
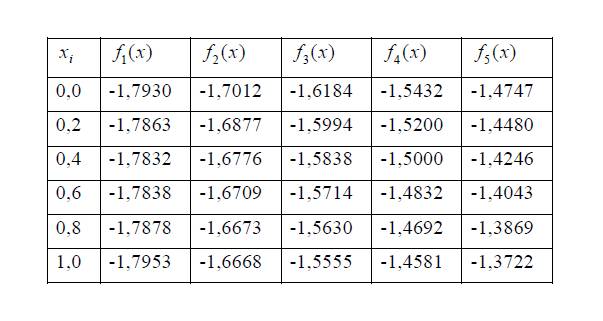
При запуске программы происходит последовательный расчет значений искомой функции в зависимости от S от первого значения f. Затем выполняется замена значений f в точках на следующее. Рассчитываются значения для всех S (от 0 до 5). Все результаты промежуточных вычислений выводятся на экран.
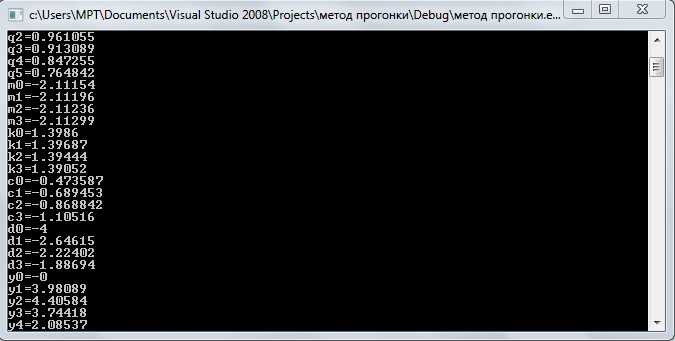
Окончательным результатом программы являются значения yi при разных значениях S и f. В ходе работы программы все полученные значения функции в шести точках (краевые значения равны нулю), номер fi, значение S записываются в файл “пакет. xls”, находящийся в корневой папке программы.
| ВеличинаS | Номер f | Y(X0) | Y(X1) | Y(X2) | Y(X3) | Y(X4) | Y(X5) |
| 0 | 1 | 0 | 3,980894 | 4,405836 | 3,744178 | 2,085366 | 0 |
| 1 | 1 | 0 | 3,815281 | 4,056137 | 3,312149 | 1,757537 | 0 |
| 2 | 1 | 0 | 3,572898 | 3,544334 | 2,705821 | 1,317501 | 0 |
| 3 | 1 | 0 | 3,485276 | 3,359318 | 2,503196 | 1,182326 | 0 |
| 4 | 1 | 0 | 3,682209 | 3,77515 | 3,00631 | 1,556194 | 0 |
| 5 | 1 | 0 | 3,976915 | 4,397435 | 3,742575 | 2,090463 | 0 |
| 0 | 2 | 0 | 3,654345 | 3,738309 | 2,965904 | 1,52744 | 0 |
| 1 | 2 | 0 | 3,76441 | 3,971378 | 3,229848 | 1,709948 | 0 |
| 2 | 2 | 0 | 3,518236 | 3,450089 | 2,601282 | 1,245099 | 0 |
| 3 | 2 | 0 | 3,341685 | 3,076232 | 2,180668 | 0,955433 | 0 |
| 4 | 2 | 0 | 3,555327 | 3,528633 | 2,722247 | 1,353371 | 0 |
| 5 | 2 | 0 | 3,761977 | 3,966227 | 3,222206 | 1,702749 | 0 |
| 0 | 3 | 0 | 3,282824 | 2,971335 | 2,073229 | 0,886283 | 0 |
| 1 | 3 | 0 | 3,558644 | 3,557061 | 2,754581 | 1,373147 | 0 |
| 2 | 3 | 0 | 3,478538 | 3,38695 | 2,534976 | 1,200369 | 0 |
| 3 | 3 | 0 | 3,227626 | 2,854118 | 1,930523 | 0,780543 | 0 |
| 4 | 3 | 0 | 3,44936 | 3,324987 | 2,488143 | 1,185269 | 0 |
| 5 | 3 | 0 | 3,528437 | 3,492915 | 2,659427 | 1,289651 | 0 |


