Использование принципа неопределенностей для оценок
Расплывание означает, что существует некая вероятность того, что частица отправится вверх или вниз, т. е. приобретет компоненту импульса, направленную вверх или вниз. (Мы говорим о вероятности и о частице, потому что дифракционную картину можно обнаружить с помощью счетчика частиц, а когда счетчик регистрирует частицу в точке не на оси, то он регистрирует ее целиком. На классическом языке это означает, что частица имеет вертикальную составляющую импульса.)
Чтобы примерно представить степень расплывания импульса, напишем, что вертикальный импульс py размазан на p0Dj. Известно, что первый минимум в дифракционной картине на щели наблюдается на таком угле Dj, что в этом направлении волна от дальнего края щели должна отстать от волны от ближнего края на свою длину. Стало быть, Dj равно l/b, и тем самым Dpy в этом эксперименте равно p0l/b. Чем меньше будет b, чем точнее будет определяться положение частицы, тем шире будет дифракционная картина.
Далее воспользуемся соотношением де Бройля — 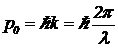 . Таким образом, можно записать следующее соотношение
. Таким образом, можно записать следующее соотношение ![]() (7)
(7)
Соотношение (1) говорит, что невозможно создать такое состояние, в котором можно было предсказать отклонение импульса частицы с точностью, превышающей 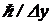 . Неопределенность в вертикальном импульсе всегда больше
. Неопределенность в вертикальном импульсе всегда больше ![]() , если Dy — неопределенность, с которой мы знаем положение частицы.
, если Dy — неопределенность, с которой мы знаем положение частицы.
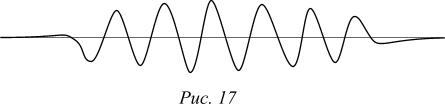 Более сложный пример поясняет связь между неопределенностью горизонтальной составляющей импульса и горизонтальной координатой. Горизонтальная координата определена с точностью Dx, если ее состояние описывается пространственно локализованным распределением амплитуды вероятности — волновым пакетом. Возможная конфигурация волнового пакета — цуг волны — изображен на рисунке 17. Вероятность обнаружить частицу везде равна нулю, кроме области, где имеется ненулевой размах амплитуды вероятности. Неопределенность горизонтальной координаты равна длине цуга L. Выясним, какова при этом неопределенность горизонтальной составляющей импульса. Ответ можно получить из анализа процесса измерения горизонтального импульса.
Более сложный пример поясняет связь между неопределенностью горизонтальной составляющей импульса и горизонтальной координатой. Горизонтальная координата определена с точностью Dx, если ее состояние описывается пространственно локализованным распределением амплитуды вероятности — волновым пакетом. Возможная конфигурация волнового пакета — цуг волны — изображен на рисунке 17. Вероятность обнаружить частицу везде равна нулю, кроме области, где имеется ненулевой размах амплитуды вероятности. Неопределенность горизонтальной координаты равна длине цуга L. Выясним, какова при этом неопределенность горизонтальной составляющей импульса. Ответ можно получить из анализа процесса измерения горизонтального импульса.
Пусть имеется широкая дифракционная решетка с большим числом N штрихов. Большое число штрихов решетки приводит к тому, что дифракционные максимумы становятся очень резкими (по сравнению с максимумами дифракции на двух щелях). Это связано с тем, что условие максимума требует, чтобы разность хода не только от соседних, но и через одну, через две щели и т. д. равнялась бы целому числу длин волн (для дифракционного максимума первого порядка — одной длине волны). Волна с точно определенной длиной волны на дифракционной решетке бесконечного размера дает как угодно узкие дифракционные максимумы. Если решетка имеет конечные размеры, то дифракционные максимумы слегка размыты. Угловой размер дифракционного максимума DJ в этом случае можно определить из условия
![]() , (8)
, (8)
где d — период решетки. Если на решетку падают две волны, длины волн которых отличаются на Dl, то, поскольку условие максимума первого порядка дается уравнением
d sinJ=l, (9)
направления на первый максимум будут отличаться на угол DJ, определяемый уравнением
dDJ cosJ=Dl Þ dDJ ~Dl. (10)
С помощью решетки ограниченных размеров не удастся различить волны с такой разницей длин волн, при которой сдвиг максимумов не превышает углового размера максимума, задаваемого уравнением (8). То есть, (8) и (10) дают 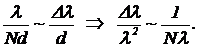 (11)
(11)
Для чего проведен данный анализ? Все дело в том, что если волна амплитуды вероятности представляет собой волновой цуг длины L, то даже бесконечного размера решетка будет действовать, как решетка конечных размеров. Действительно, части рассеянного цуга в направлении дифракционного максимума будут налагаться друг на друга только в том случае, если они находятся на расстоянии Nl поперек щелей, не превышающем длины цуга, т. е. ![]() . Следовательно, цуг волны длиной L представляет собой смесь волн с разными длинами. Он имеет неопределенность длины волны
. Следовательно, цуг волны длиной L представляет собой смесь волн с разными длинами. Он имеет неопределенность длины волны
![]() (12)
(12)
Заметим, что 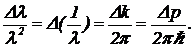 (13) Таким образом, соотношение (11) с учетом уравнения (13) можно переписать так
(13) Таким образом, соотношение (11) с учетом уравнения (13) можно переписать так ![]() (14)~
(14)~
Теперь вспомним, что L — неопределенность горизонтальной координаты частицы, а Dp — неопределенность горизонтальной составляющей импульса Dpx. Так что опять получаем
DpxDx~ћ. (15)
Соотношения (7) и (15) указывают пределы применимости классических представлений об импульсе и координате частицы.
3.2 Использование принципа неопределенностей для оценок
Соотношения (7) и (15) дают мощное эвристическое средство для квантовых оценок характерных масштабов и значений энергий микроскопических физических систем. Рассмотрим два примера применения этого принципа.
Задача 4. Допустим, к примеру, мы решили удерживать частицу массы m в области размером b. Для этого по обе стороны частицы поставили две жесткие пластинки и стали очень медленно сближать их. Задача состоит в том, чтобы выяснить, какова будет реакция частицы на эту процедуру.
Решение. Положение частицы имеет неопределенность Dx=b. Частица в этих условиях не может находиться в покое. Ее импульс будет иметь неопределенность
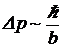 . (16)
. (16)
А так как в среднем частица остается на месте, такие же характерные значения имеет и импульс частицы. Таким образом, следует ожидать, что характерные значения кинетической энергии частицы E=p2/2m будут такими:
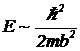 (17)
(17)
— при уменьшении расстояния между пластинками энергия частицы увеличивается. То есть, чтобы сблизить пластинки надо совершить работу. Из этого следует, что частица создает давление на пластинки. Чтобы локализовать распределение амплитуд вероятности частицы в области бесконечно малых размеров, надо совершить бесконечно большую работу.
Проведенный анализ показывает, что распределение амплитуд вероятности частицы обладает упругостью, как какая-нибудь упругая среда. Это налагает определенные ограничения на поведение и на возможные конфигурации распределений. В частности изменение распределения амплитуд в пространстве должно быть плавным, без резких скачков и разрывов.
Из (17) так же следует, что тяжелую частицу локализовать в малой области пространства легче, чем частицу меньшей массы. По этой причине мюоноводород (водород, в котором роль электрона играет мюон, который в 207 раз тяжелее электрона) имеет размеры гораздо меньшие, чем настоящий водород.
Задача 4. Используя соотношение неопределенностей импульса и координаты оценить энергию основного состояния атома водорода и его размер.
Решение. Так как масса электрона много меньше массы протона, будем считать, что движется только электрон, а протон покоится. В основу расчетов возьмем положение о том, что система, предоставленная сама себе, оказывается в состоянии с наименьшей энергией. Полная энергия электрона равна сумме кинетической и потенциальной энергий:
E=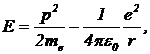 (18)
(18)
где r — расстояние между электроном и протоном. Так как в связанном состоянии электрон не улетает далеко от протона, можно считать, что это расстояние равно размеру области локализации электрона, т. е. неопределенности координаты. В таком случае импульс электрона имеет неопределенность
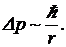 (19)
(19)
А так как в среднем частица остается на месте, такие же характерные значения имеет и сам импульс частицы. Таким образом, следует ожидать, что характерные значения полной энергии частицы должны удовлетворять соотношению: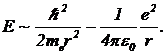 (20)
(20)
При уменьшении размера r потенциальная энергия убывает пропорционально —1/r, а кинетическая энергия возрастает пропорционально 1/r2. Значит, должно существовать оптимальное значение r, при котором полная энергия принимает наименьшее значение. Оно определится из условия минимума: 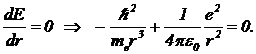 (21)
(21)
Из уравнения (21) находим оптимальный размер области локализации электрона 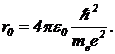 (22)
(22)
Нетрудно увидеть, что это выражение точно совпадает с выражением первого боровского радиуса. Подстановка значений констант дает r0=
=0,53×10-10 м.


