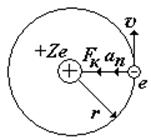
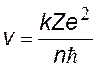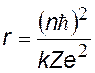Изменение длины волны при комптоновском рассеянии
изменение длины волны при комптоновском рассеянии излучения (на свободном электроне)
Из формул следует, что комптоновское изменение длины волны не зависит от природы рассеивающего вещества, а определяется только углом наблюдения.
|
|
Эта величина называется комптоновской длиной волны электрона |
Комптоновское рассеяние может наблюдаться и на свободном протоне, тогда следует использовать комптоновскую длину волны протона: 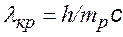
Из формулы (¨) следует, что изменение l при различных углах рассеяния равно:
|
q = 0о |
Dl = 0 |
фотоны, продолжающие лететь в первоначальном направлении, не изменяют свою длину волны |
|
q = 90о |
Dl = |
в этом случае изменение l равно комптоновской длине волны электрона |
|
q = 180о |
Dl = |
максимальное изменение l происходит в случае, когда рассеянный фотон движется в противоположном направлении |
Ниже приводится таблица формул, используя которые можно получить выражение (¨) для Dl. Компактное расположение формул облегчает также решение задач.
|
|
|
энергия падающего и рассеянного фотонов |
|
|
|
импульс —²— |
|
|
релятивистская кинетическая энергия электрона отдачи |
|
|
|
по этой формуле можно найти угол отдачи j |
Комптоновское рассеяние наблюдается только для рентгеновских и гамма-лучей. В этом случае изменение длины волны сравнимо с длиной волны падающего излучения, и может быть измерено экспериментально. Для видимого света обнаружить эффект Комптона невозможно, т. к. максимальное изменение Dl = 0,48 пм слишком мало по сравнению со средней длиной световой волны
l » 500 нм = 500000 пм (зеленый свет) и перекрывается тепловым уширением спектральных линий..
Эффект Комптона доказывает, что: 1) свет имеет квантовую природу и
2) для элементарных процессов взаимодействия частиц применимы законы сохранения импульса и энергии.
ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ АТОМОВ И МОДЕЛЬ АТОМА БОРА.
Ядерная модель атома.
Резерфорд на основании опытов по рассеянию альфа-частиц на металлической фольге (1909-10 гг.) предложил ядерную (планетарную) модель атома. Атом представляет собой очень маленькое ядро, в котором сосредоточена почти вся масса атома, а вокруг ядра вращаются электроны подобно планетам солнечной системы. Эта модель оказалась несостоятельной, она не могла объяснить, почему спектры излучения газов состоят из отдельных линий, а не являются сплошными. Электроны, обладающие ускорением, должны непрерывно излучать электромагнитные волны, терять энергию и, в конце концов, упасть на ядро. Однако атомы являются устойчивыми системами.
В 1913 г Бор дополнил модель Резерфорда, выдвинув принципиально новые предположения (постулаты).
Постулаты Бора:
|
1 |
В атомах существуют особые стационарные орбиты, на которых электрон может двигаться сколь угодно долго. |
Целые числа При n = 1 |
|
Момент количества движения (момент импульса) электрона на таких орбитах равен:
|
||
|
2 |
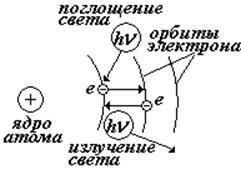
При переходе электрона с одной стационарной орбиты на другую происходит излучение (или поглощение) кванта энергии.
Е – энергия электрона на орбите |
|
Теория Бора может быть названа полуклассической, полуквантовой. В этой теории движение электрона на орбите описывалось классическими законами (формулы – см. дальше). Вместе с тем, теория приводила к тому, что скорость, радиус орбиты, энергия электрона не могут иметь любые значения, а квантуются, т. е. могут принимать только дискретные (отдельные) значения.
Теория Бора хорошо описывала закономерности в спектре атома водорода и водородоподобных атомов.(Водородоподобными атомами называют атомы (или ионы) у которых на последней орбите имеется только один электрон). Однако, для атома гелия (Z = 2) и других элементов теория Бора не давала совпадения с опытом.
Атом водорода и водородоподобные атомы (ВПА) по теории Бора.
На рис. показан водородоподобный атом. Заряд ядра равен +Ze, где Z число протонов (и номер элемента в таблице Менделеева). Вокруг ядра вращается по круговой орбите электрон е со скоростью v. На электрон действует со стороны ядра кулоновская сила Fкул. Запишем II закон Ньютона для электрона: man=Fкул., где an = v2/ r — нормальное ускорение. (Взаимодействие электрона с другими электронами атома не учитываем).
|
|
II закон Ньютона и закон Кулона, к=1/4peо – коэффициент в СИ |
|
Для атома водорода Z = 1 |
|
|
постулат Бора |
Из этих формул получим выражения для скорости v и радиуса r орбиты электрона. Сократим в уравнении (z) на r, а оставшующуюся r перенесем в числитель левой части уравнения. Затем разделим уравнение (z) на (y) и получим v. Подставим v в (y) и найдем r.
Внимание! Легче запомнить вывод формул для v и r, чем сами формулы для них.
|
|
скорость электрона на орбите, квантуется как v ~ 1/n; v1 = 2,2×106 м/с |
|
|
радиус орбиты электрона, квантуется как r ~ n2 r1 = 0,53 нм – первый боровский радиус |
Когда электрон в атоме Н находится на 1-ой орбите, говорят, что электрон (или атом) находится в основном (невозбужденном) состоянии, при этом электрон имеет минимальную энергию. Все остальные состояния называются возбужденными состояниями.
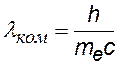 = 2,43 пм = 2,43×10-12 м
= 2,43 пм = 2,43×10-12 м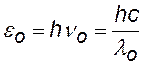
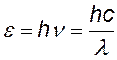
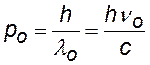
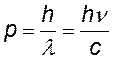
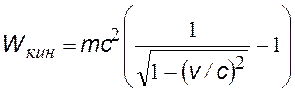
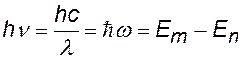
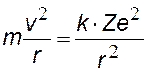 z
z