Измерение радиоактивности

4. Решение задач

Задача 1. Определите период полураспада радона, если за 1 сутки из 106 ядер распадается 175000 штук.

Решение. При решении задачи используем закон радиоактивного распада: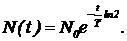
(8)
Из него следует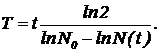
(9)
Через сутки останется N(t)=106 –0,175×106=0,825×106. Подстановка дает
×

Задача 2. Период полураспада одного из изотопов йода составляет 8 суток. Через какое время число атомов этого изотопа уменьшится в 100 раз?

Задача 3. Удельное содержание радиоактивного изотопа , усвоенного деревом при его росте, остается постоянной величиной вплоть до его гибели. В погибшем дереве содержание начинает уменьшаться вследствие b—распада. Определите возраст деревянного предмета, обнаруженного при археологических раскопках, если активность, приходящаяся на единицу массы вещества, составляет 0,1 удельной активности свежесрубленного дерева. Период полураспада изотопа равен 5730 годам.

Решение. Задача поясняет метод радиоуглеродного определения возраста археологических находок и возраста различных осадочных пород. Перед началом решения ознакомимся с идеей метода.

Нейтроны, содержащиеся в космических лучах, налетают на атомы азота атмосферы, которые могут превращаться в атомы углерода по схеме
(10)
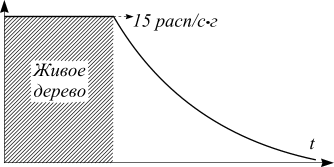
Изотоп углерода является радиоактивным с периодом полураспада 5730 лет. Образующиеся в верхних слоях атмосферы изотопы перемешиваются с воздухом, окисляются до CO2. При постоянном потоке космических лучей устанавливается динамическое равновесие между подпиткой атмосферы вновь рождающимися атомами радиоактивного углерода и убылью за счет распадов. Растения усваивают углерод в виде углекислого газа, и отношение скорости усвоения с радиоактивным изотопом к скорости усвоения обычного CO2 остается постоянной. Так что радиоактивный углерод, участвующий в жизненных циклах растений и животных, имеет строго определенную концентрацию. При установившемся значении концентрации активность равна, примерно, 15 распадам на один грамм углерода в секунду органического происхождения. Это активность живого растения. Определяя активность углерода органического происхождения после гибели растения, можно определить время, прошедшее после гибели.

Следуя идее решения предыдущей задачи, имеем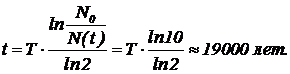

Задача 4. Определить период полураспада радия, если известно, что кусочек радия массой 1 г выбрасывает 3,7×1010 a-частиц за одну секунду.

Задача 5. Определите число распадных электронов, испускаемых 1 кг изотопа фосфора за одни сутки. Период полураспада изотопа равен 14 суткам.

5. Домашнее задание

5.2 Решение задач

Задача 1. В периодической системе элементов рядом расположены три элемента. Условно назовем их a, b, c. Радиоактивный изотоп элемента a превращается в изотоп элемента b, а тот, в свою очередь, — в изотоп элемента c. Последний превращается в изотоп исходного элемента a. Какими процессами обусловлены эти превращения?

Задача 2. В микрокалориметр с теплоемкостью 1000 Дж/К помещено 100 мг изотопа кобальта (атомная масса 61). При распаде одного ядра кобальта выделяется энергия 2×10-19 Дж. Через 50 мин температура калориметра повысилась на 0,06 К. Пренебрегая тепловыми потерями, найдите период полураспада изотопа кобальта.

Задача 3. При распаде урана-238 массой 1 кг излучается 1,24×107 a-частиц за одну секунду. Определите период полураспада этого изотопа.

занятие 2.2.4

измерение радиоактивности

1. Обсуждение домашнего задания

2. Решение задач

Задача 1. В цепочке радиоактивных превращений элемента с порядковым номером 92 и атомной массой 235 в элемент порядковым номером 82 и атомной массой 207 (уран-235 в свинец-207) имеется несколько a-распадов и b-распадов. Сколько всего распадов в этой цепочке?

Решение. Пусть произошло n этапов a-распадов и k этапов b-распа­дов. Из закона сохранения заряда, следует
92-2n+k=82
Из закона сохранения барионного заряда —
235-4n=207

Совместное решение системы дает: k=4; n=7. Всего одиннадцать звеньев в цепочке распадов.

Задача 2. Изотоп плутония a-радиоактивен. Процесс его распада идет следующим образом: При этом распаде освобождается энергия, большая часть которой идет на кинетическую энергию a-частиц. Однако часть энергии оказывается в ядре урана, которое сбрасывает ее, испуская фотон. Определите скорость вылета a-частиц, если фотон уносит 0,09 МэВ. Массы ядер, участвующих в реакции, в углеродных единицах следующие:
mPu=239,05122 а. е.м., mU=235,04299 а. е.м., mHe=4,00260 а. е.м.

Решение. Разность дефектов масс левой и правой частей реакции равна
DM=239,05122-235,04299-4,00269=0,00563 (а. е.м.)
Энергетический выход реакции
Eвых=DMc2 (Дж) или DM×931,5 (МэВ)=5,24 МэВ.
Энергия a-частицы
Ea=Eвых-Eg=5,24-0,09=5,15 МэВ=8,24×10-13 Дж.
Скорость a-частицы —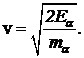

Подстановка дает v»1.6×107 м/с, что составляет примерно 0,05 с. Частица нерелятивистская.

Задача 3. Азот облучается в течение одного часа пучком a-частиц. Найдите количество атомов образовавшегося изотопа , если ток в пучке 2×10-4А и ядерную реакцию превращения азота в кислород вызывает одна частица из каждых ста тысяч в пучке.

3. Измерение радиоактивности

3.1 Определение и примеры

Радиоактивностью, или просто активностью, называют величину, пропорциональную скорости радиоактивного распада вещества.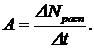
(1)
Она измеряется в кюри (Ku) или в резерфордах (Рф):
1 Ku=3,7×1010 расп/с; 1 Рф=106 расп/с. (2)

Задача 4. В свинцовой капсуле находится 4×1018 атомов радия. Определите активность данного количества радия, если период полураспада равен 1620 годам.

Решение. Требуется определить число распадов в одну секунду, а период полураспада — годы, поэтому заведомо выполняется . Так что можно воспользоваться формулой из прошлого занятия:

Задача 5. Имеется урановый препарат с активностью 0,56 mKu. Определите количество изотопа в препарате, если его период полураспада 7,1×108 лет.

Решите задачу для самоконтроля.

Задача 6. В капсуле находится 0,15 моля изотопа плутония . Определите активность данного количества плутония, если его период полураспада равен 2,44×104 лет.