Капельная модель ядра

3. Домашнее задание

Проработать материал предыдущих занятий, просмотреть решения задач и подготовиться к контрольной работе.

занятие 2.2.5

контрольная работа “атомное ядро”

вариант i

Задача 1. Допишите ядерные реакции:
.

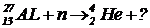Задача 2. Поглощается или освобождается энергия в реакции —

Задача 3. Ядро изотопа урана , захватив нейтрон, разделилось на два осколка. При этом освободилось два нейтрона. Один из осколков оказался ядром изотопа ксенона . Каким был второй осколок?

Задача 4. Изотоп плутония распадается по схеме: 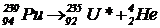. При этом распаде освобождается энергия, большую часть которой составляет кинетическая энергия a-частицы. Однако часть энергии оказывается в ядре урана, которое сбрасывает ее, излучая фотон. Определить скорость a-частицы, если фотон уносит 0,09 МэВ. Массы ядер, участвующих в реакции, в углеродных единицах следующие:
mPu=239,05122 а. е.м., mU=235,04299 а. е.м., mHe=4,00260 а. е.м.

Задача 5. Какая доля радиоактивных ядер кобальта, период полураспада которых 73,3 дня, распадается за месяц?

Задача 6. Определите возраст минерала, в котором на один атом урана-238 приходится один атом свинца. Предположите, что в момент образования минерала в нем не было свинца, а промежуточные реакции распада идут много быстрее, чем распад урана-238. Период полураспада урана-238 равен 4,5×109 лет.

Задача 7. При слиянии протона с ядром трития образуются a-частица и фотон: 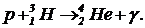Дефект масс составляет 0,0304 а. е.м. Кинетическая энергия частиц, образующихся в реакции на 11,3 МэВ больше, кинетической энергии исходных частиц. Определите энергию, уносимую фотоном в первой реакции, если кинетическими энергиями p, и можно пренебречь.

вариант ii

Задача 1. Допишите ядерные реакции:
.

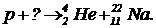Задача 2. Поглощается или освобождается энергия в реакции —

Задача 3. Ядро изотопа урана , захватив нейтрон, разделилось на два осколка. При этом освободилось четыре нейтрона. Один из осколков оказался ядром изотопа цезия . Каким был второй осколок?

Задача 4. Кинетическая энергия a-частицы, вылетающей из ядра атома полония при радиоактивном распаде, равна 7,68 МэВ. Определите полную энергию распада и скорость осколка.

Задача 5. Определите время, за которое распадается радий, если его начальная масса Mo=1 г, а конечная 5 мкг, T1/2=1620 лет.

Задача 6. Измерения активности углерода в органических находках на стоянках человека в Северной Америке показали, что она равна примерно 4,23 распада/с на 100 г углерода. . Концентрация радиоактивного углерода в живом растении такова, что происходит 15 распадов в секунду на 1 г углерода. Период полураспада углерода-14 равен 5730 г. Чему равен возраст найденных стоянок?

Задача 7. При слиянии протона с ядром дейтерия образуются ядро и фотон: 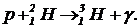Энергия фотона много больше энергии p, и . Кинетическая энергия частиц, образующихся в реакции 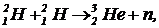на 3,3 МэВ больше, кинетической энергии исходных частиц. Определите дефект масс ядра в а. е.м. Одной а. е.м. соответствует 931,5 МэВ.

Таблица значений энергии связи некоторых ядер

занятие 2.2.6

капельная модель ядра

2. Цепные реакции деления

2.1 Капельная модель ядра

Одной из главных характеристик ядра является его масса, которая определяется массовым числом A. Масса ядра M немногим меньше суммы масс протонов mp и нейтронов mn, входящих в него. Число протонов в ядре обозначается буквой Z, а число нейтронов — через N. Число протонов в ядре определяет его заряд q=Ze и также является характеристикой ядра. Масса ядра равна Zmp+mnN—DM, где DM — дефект массы. Дефект массы является следствием межнуклонного притяжения. Чтобы разобрать ядро на составные части надо совершить работу W против сил притяжения, равную энергии связи ядра. Ясно, что энергия ядра в разобранном состоянии (Zmp+mnN)c2 больше энергии ядра как такового Mc2 на W:
(Zmp+mnN)c2-Mc2=W. (1)
Очевидно, что
W=DMc2. (2)
Дефект массы, таким образом, является мерой прочности ядра, а ос­новная его характеристика — масса — определяет энергию связи. Например, измерения массы ядра изотопа лития 6Li с помощью масс-спектрометра показали, что его масса равна 5601,42 МэВ. Масса входящих в него трех протонов и трех нейтронов равна 3mpc2+3mnc2=3×938,28+3×939,57=5633,55 МэВ, следовательно, энергия связи ядра данного изотопа равна 5633,55-5601,42=32,13 МэВ. Из вышеизложенного ясно, сколь важны точные измерения масс элементов с помощью высокоточных масс-спектрометров.

Одно из наиболее удивительных свойств ядер заключается в том, что, начиная с массовых чисел в несколько десятков, энергия связи, приблизительно, пропорциональна массовому числу A (энергия, приходящаяся на один нуклон, одна и та же). Это свойство обязано малому радиусу адронного взаимодействия между нуклонами. Каждый нуклон взаимодействует только с ближайшими соседями. Ситуация такая же, как в жидкости, где также имеет место межмолекулярное взаимодействие только между ближайшими соседями. Энергия связи устойчивых ядер, отнесенная к одному нуклону, как функция массового числа, имеет вид, изображенный на рисунке 32. В области малых значений массового числа энергия связи значительно ниже среднего уровня. Максимума зависимость достигает в районе значений массового числа ядра железа (60). При дальнейшем увеличении A энергия связи плавно уменьшается.