Кинематика теории относительности
Аналогично проведенному решению из факта инвариантности интервала можно получить преобразование длин.
3. Решение задач
Задача 4. Пусть вдоль проводника с током, на некотором расстоянии r от оси в том же направлении, что и электроны проводимости провода, летит электрон. Полный заряд провода равен нулю, т. к. положительные заряды ионов точно компенсируются зарядами электронов проводимости. Движущийся со скоростью v электрон испытывает действие силы Лоренца
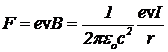 . (13)
. (13)
Положим, что скорости наружного электрона и электронов проводимости равны. Найдите силу взаимодействия электрона с проводом в системе отсчета, в которой электрон покоится.
Задача 5. Положим, что скорость самолета равна 1000 км/час. Оцените, на сколько задерживается старение пассажира, совершающего поездку Красноярск — Москва. Полагайте, что расстояние между Красноярском и Москвой равно 4000 км.
Задача 6. В лабораторной системе отсчета частицы движутся навстречу друг другу с одинаковыми скоростями v. При каких значениях v вычисление относительной скорости с помощью принципа Галилея дает ошибку, не превышающую 1%?
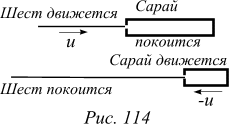 Задача 7. Возьмем шест длиной 20 м и будем двигать его в направлении его длины с такой скоростью, при которой его длина в лабораторной системе отсчета оказалась равной 10 м. Тогда в некоторый момент времени он целиком может спрятаться в сарае длиной 10 м. Но из системы отсчета, в которой шест покоится, наполовину сократившимся, является не шест, а сарай. Ясно, что 20-метровый шест невозможно спрятать в 5-метровом сарае. Имеет ли место противоречие в описанной ситуации? Используя преобразования Лоренца, покажите, как без противоречий должна рассматриваться данная ситуация.
Задача 7. Возьмем шест длиной 20 м и будем двигать его в направлении его длины с такой скоростью, при которой его длина в лабораторной системе отсчета оказалась равной 10 м. Тогда в некоторый момент времени он целиком может спрятаться в сарае длиной 10 м. Но из системы отсчета, в которой шест покоится, наполовину сократившимся, является не шест, а сарай. Ясно, что 20-метровый шест невозможно спрятать в 5-метровом сарае. Имеет ли место противоречие в описанной ситуации? Используя преобразования Лоренца, покажите, как без противоречий должна рассматриваться данная ситуация.
Решение. Анализ ситуации полезно провести, используя преобразования Лоренца, рассматривая события: совмещение переднего конца шеста с задней стенкой сарая и совмещение заднего конца шеста со входом в сарай, с двух точек зрения — с позиций наблюдателя из системы отсчета, связанной с сараем и из системы отсчета, связанной с шестом.
Пусть собственная длина шеста равна L, тогда длина сарая — L/2. Чтобы длина шеста из системы отсчета, связанной с сараем, оказалась равной L/2, шест должен двигаться со скоростью ![]() . Поместим начала координат обеих систем отсчета в точку соприкосновения переднего конца шеста и задней стенки сарая и будем считать момент соприкосновения начальным моментом времени в обеих системах отсчета t1=t`1=0. Рассмотрим два события: первое событие — “передний конец шеста совместился с задней стенкой сарая (оказался в начале координат)”; второе событие — “задний конец шеста совместился со входом в сарай”. Координаты первого события в обеих системах отсчета одинаковы и равны: x1=x`1=0, t1=t`1=0. Координаты второго события естественнее определить в системе отсчета, связанной с сараем, так как в этой системе отсчета и первое и второе события происходят одновременно.
. Поместим начала координат обеих систем отсчета в точку соприкосновения переднего конца шеста и задней стенки сарая и будем считать момент соприкосновения начальным моментом времени в обеих системах отсчета t1=t`1=0. Рассмотрим два события: первое событие — “передний конец шеста совместился с задней стенкой сарая (оказался в начале координат)”; второе событие — “задний конец шеста совместился со входом в сарай”. Координаты первого события в обеих системах отсчета одинаковы и равны: x1=x`1=0, t1=t`1=0. Координаты второго события естественнее определить в системе отсчета, связанной с сараем, так как в этой системе отсчета и первое и второе события происходят одновременно. 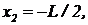 t2=0. (9) Определим, координаты входа в сарай в системе отсчета, связанной с шестом.
t2=0. (9) Определим, координаты входа в сарай в системе отсчета, связанной с шестом. 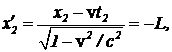
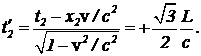 (10) Как видно, совмещение заднего конца шеста со входом в сарай происходит не одновременно с совмещением переднего конца. Легко определить, что за время t`2 от момента совпадения переднего конца шеста с задней стенкой сарай переместился на расстояние
(10) Как видно, совмещение заднего конца шеста со входом в сарай происходит не одновременно с совмещением переднего конца. Легко определить, что за время t`2 от момента совпадения переднего конца шеста с задней стенкой сарай переместился на расстояние 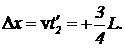 Так что координата входа в сарай в момент времени t`2=0 равна . Это согласуется с точкой зрения наблюдателя из системы отсчета, связанной с шестом, согласно которой, длина сарая уменьшается до
Так что координата входа в сарай в момент времени t`2=0 равна . Это согласуется с точкой зрения наблюдателя из системы отсчета, связанной с шестом, согласно которой, длина сарая уменьшается до ![]() . Но при этом мы должны иметь в виду, что совмещение заднего конца шеста и входа в сарай в обеих системах отсчета является одним и тем же событием. Отличие точек зрения состоит в том, что совмещения обоих концов шеста в одной системе отсчета являются одновременными, а в другой — те же самые события неодновременные. То есть, в условии задачи речь идет не об одной и той же паре событий.
. Но при этом мы должны иметь в виду, что совмещение заднего конца шеста и входа в сарай в обеих системах отсчета является одним и тем же событием. Отличие точек зрения состоит в том, что совмещения обоих концов шеста в одной системе отсчета являются одновременными, а в другой — те же самые события неодновременные. То есть, в условии задачи речь идет не об одной и той же паре событий.
3. Домашнее задание
Подготовиться к самостоятельной работе — проработать решенные на занятиях 1.5.1 — 1.5.4 задачи.
занятие 1.5.5
самостоятельная работа
“кинематика теории относительности”
Задача 1. Пионы от рождения до распада оставляют в пузырьковой камере следы, среднее значение длины которых равно 8 м. Чему равно среднее значение собственного времени жизни, если начальная скорость всех пионов одинакова и равна v=0,73×c?
Задача 2. В результате непрерывно происходящей на Солнце термоядерной реакции из него истекает поток нейтронов. Собственное среднее время жизни нейтрона равно 1,01×103 секунды. При каких условиях одна треть вылетевших нейтронов долетит до Земли, если расстояние от Земли до Солнца равно 1,5×1011 м?
Задача 3. Два параллельных пучка электронов, несущих ток 2 А, находятся на расстоянии 10 см. Скорость электронов пучка составляет 0,9999×c. Чему равна сила взаимодействия пучков, рассчитанная на единицу длины, в лабораторной системе отсчета и в системе отсчета, в которой электроны покоятся?
Задача 4. При попадании Земли в пояс астероидов наблюдается большое число падающих звезд. Полагая, что Земля и астероиды движутся навстречу друг другу, определите их относительную скорость, если скорости Земли и астероидов относительно Солнца равны соответственно 30 км/с и 60 км/с. Какой можно сделать вывод из полученного результата?
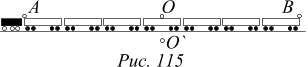 Задача 5. Пусть на поезде, движущемся со скоростью v, близкой к скорости света, едут три человека (A, O и B). A едет в голове поезда, O в середине, а B – в хвосте. Вблизи железнодорожного полотна стоит четвертый человек O`. В тот самый момент, когда O поравнялся с O`, сигналы ламп-вспышек от A и B достигают O и O`. Кто первым послал сигнал? Пользуясь преобразованиями Лоренца или другим путем, вычислите разницу между моментами времени, когда послали сигналы A и B, наблюдаемую в системе отсчета поезда (DtAB) и в системе отсчета O` (Dt`AB)`.
Задача 5. Пусть на поезде, движущемся со скоростью v, близкой к скорости света, едут три человека (A, O и B). A едет в голове поезда, O в середине, а B – в хвосте. Вблизи железнодорожного полотна стоит четвертый человек O`. В тот самый момент, когда O поравнялся с O`, сигналы ламп-вспышек от A и B достигают O и O`. Кто первым послал сигнал? Пользуясь преобразованиями Лоренца или другим путем, вычислите разницу между моментами времени, когда послали сигналы A и B, наблюдаемую в системе отсчета поезда (DtAB) и в системе отсчета O` (Dt`AB)`.
занятие 1.6.1
релятивистский импульс
2. Релятивистский импульс
2.1 Постановка задачи
Импульс частицы является одной из самых важных величин в механике. При действии силы на частицу ее импульс увеличивается. Как было выяснено на предыдущих занятиях, скорость частицы не может превышать скорости света. В свете этого факта классическая формула для импульса p=mv выглядит подозрительной. Из-за ограничения скорости классическая формула при произвольно длительном действии силы не даст импульс более, чем mc. Вероятно, формула p=mv должна быть исправлена.
Цель работы на данном этапе состоит в подборе такого выражения импульса частицы, чтобы при v<<c из него получалась классическая формула: p=mv, и чтобы оставался справедливым закон сохранения импульса для замкнутых систем в любой инерциальной системе отсчета.
2.2 При классическом определении импульс не сохраняется
 Рассмотрим упругое столкновение двух частиц, полагая, что p=mv. Пусть
Рассмотрим упругое столкновение двух частиц, полагая, что p=mv. Пусть ![]() и
и ![]() — импульсы частиц в системе центра масс до столкновения,
— импульсы частиц в системе центра масс до столкновения, ![]() и
и ![]() — после столкновения. По определению
— после столкновения. По определению 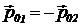 и
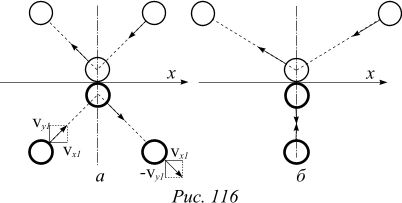
и 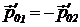 . При упругом столкновении изменяется только направление импульса, поэтому при выборе системы координат так, как показано на рисунке 116 а, изменение импульса первой частицы равно
. При упругом столкновении изменяется только направление импульса, поэтому при выборе системы координат так, как показано на рисунке 116 а, изменение импульса первой частицы равно ![]()
![]() . Изменение импульса второй частицы —
. Изменение импульса второй частицы — 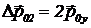 . Полное изменение импульса равно нулю:
. Полное изменение импульса равно нулю: