Бозоны и фермионы

Задача 2. Молекулы гелия, прилипшие к стенкам сосуда образуют двухмерный газ. Энергия отрыва молекулы от стенки равна 10-4 эВ. Чему равен показатель адиабаты для прилипшего к стенке гелия? При какой характеристической температуре произойдет переход гелия в нормальное состояние?

Задача 3. По классической теории, твердое тело представляет собой большую систему связанных осцилляторов. На одну колебательную степень свободы в состоянии теплового равновесия приходится энергия kБT. Чему равна молярная теплоемкость кристалла по классическим соображениям? Качественно объясните уменьшение теплоемкости кристалла при низких температурах.

занятие 2.1.13

тождественные частицы

2. Бозоны и фермионы

2.1 Двухчастичные состояния

Один из наиболее поразительных принципов квантовой механики относится к описанию состояний многих частиц. Чтобы понять его содержание, рассмотрим опыт по рассеянию двух частиц друг на друге в системе центра масс.

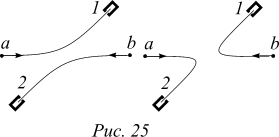Представим, что сталкиваются две разные частицы a и b и частица a рассеивается в направлении 1, а частица b — направлении 2. Пусть f(J) — амплитуда этого процесса; тогда вероятность P1 наблюдения данного события равна |f(J)|2. Могло случиться, конечно, что частица b рассеялась в счетчик 1, а частица a — в счетчик 2. Вероятность этого события равна была бы в этом случае |f(p—J)|2. Если нас интересует вероятность срабатывания детектора 1, вне зависимости от того, какая частица в него попала, то эта вероятность будет равна сумме вероятностей попадания или частицы a, или частицы b: Pразн=|f(J)|2+|f(p—J)|2. Рассмотрим теперь, что случится, если рассеиваются идентичные частицы, например, две a-частицы. Удивительно, что в природе рассеяние происходит так, как будто попадание частицы a в детектор 1 и попадание частицы b в этот детектор являются двумя способами осуществления одного и того же события. Амплитуда срабатывания детектора равна сумме амплитуд попадания в него частицы a или частицы b. Вероятность срабатывания детектора 1 равна
Pтожд=|f(J)+f(p—J)|2. (1)
Например, если J=p/2, то вероятность срабатывания детектора 1 при рассеянии тождественных частиц
(2)
оказывается в два раза большей, чем при рассеянии нетождественных частиц.

Амплитуда процесса, в котором участвуют две тождественные частицы, равна сумме амплитуды осуществления этого процесса и амплитуды процесса, в котором частицы обменялись ролями:

(Амплитуда процесса)+(Амплитуда обмена) (3)

Надо сказать, что существует еще один класс тождественных частиц. В отличие от a-частиц амплитуда того, что произойдет процесс, в котором участвуют две тождественные частицы этого класса, равна разности амплитуды процесса и амплитуды процесса, в котором частицы обменялись ролями.

(Амплитуда процесса)-(Амплитуда обмена) (4)

Частицы, поведение которых описывается амплитудами, интерферирующими в фазе, называются бозе-частицами или бозонами, а частицы, поведение которых описывается амплитудами, интерферирующими в противофазе, называются ферми-частицами или фермионами. Ниже приведена таблица бозонов и фермионов.

Все бозоны имеют спин, равный целому числу единиц постоянных Планка, а фермионы — полуцелому.

Вывод: амплитуда процесса, в котором участвуют два бозона равна сумме амплитуды осуществления этого процесса и амплитуды процесса, в котором частицы обменялись ролями, а амплитуда процесса, в котором участвуют два фермиона, равна разности амплитуды осуществления этого процесса и амплитуды процесса, в котором частицы обменялись ролями.

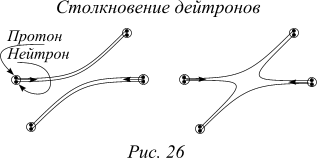Интересная ситуация возникает при наличии двух или более тесно связанных частиц. К примеру, дейтрон состоит из протона и нейтрона. Когда рассеиваются два дейтрона, может представиться несколько возможностей. Может случиться, что при столкновении нейтрон первого дейтрона перескочит к встречному, а нейтрон встречного перескочит к первому. Так что после рассеяния два дейтрона оказываются не первоначальными частицами — произошел обмен парой нейтронов. Амплитуда рассеяния с обменом парой нейтронов будет интерферировать с амплитудой рассеяния без такого обмена, и интерференция должна иметь знак минус, потому, что состоялся обмен фермионами. С другой стороны, если энергия сталкивающихся дейтронов так мала, что они из-за кулоновского расталкивания не могут значительно сблизиться, то дейтрон в таком случае можно считать простейшим объектом, не задумываясь о деталях внутреннего строения. В этих условиях в амплитуду рассеяния войдут только два члена. Либо обмена вовсе нет, либо при рассеянии происходит обмен всеми двумя нуклонами. Каждая пара изменяет знак, и в итоге амплитуды складываются со знаком плюс. Так что дейтрон ведет себя, как бозон.

Таким образом, правило состоит в том, что сложные объекты в тех обстоятельствах, когда их можно считать неделимыми объектами, ведут себя, как бозоны или как фермионы, смотря по тому, содержится в них четное или нечетное число фермионов. К примеру, во всех атомных процессах ядра гелия 4He (a-частица) ведут себя, как бозоны, так как содержат два протона и два нейтрона. А вот ядра изотопов гелия три — 3He — во всех атомных процессах ведут себя, как фермионы, так как содержат два протона и один нейтрон.

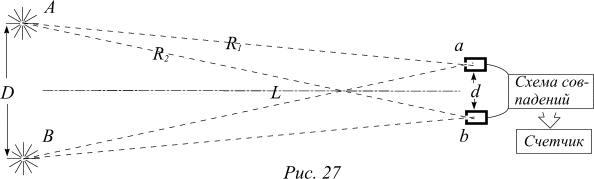Задача 1. Диаметр ближайших к Земле звезд слишком мал, и его нельзя определить даже при помощи лучших современных телескопов, поскольку их угловое разрешение больше “углового диаметра” звезд. Диаметр звезд впервые определил Майкельсон, используя оптический интерферометр. Но точности этого метода едва хватает для самых близких звезд. В 1956 г. Браун и Твисс предложили новый метод для таких измерений. Они опробовали его на звезде Сириус. Для этого они взяли два параболических рефлектора, в фокусе каждого из которых был установлен фотоумножитель. Выходы фотоумножителей соединялись с электронной схемой, которая пересчитывала случаи совпадения попадания фотонов в оба фотоумножителя. По поведению скорости счета совпадений в зависимости от расстояния между приемниками определялся угловой размер звезды. В то время многие физики утверждали, что этот метод не годится, поскольку свет — это фотоны, а каждый фотон попадает либо в один, либо в другой приемник, и никаких интерференционных эффектов в совпадении попаданий не должно быть. Вы можете опровергнуть этот аргумент, рассматривая следующий идеализированный эксперимент. Два небольших источника света A и B находятся очень далеко от фотоумножителей a и b. Геометрические условия опыта показаны на рисунке. С детекторами a и b соединены счетчики, сосчитывающие числа фотонов P1 и P2, регистрируемых в секунду каждым счетчиком. Счетчики a и b включены, кроме того, еще в “схему совпадений”, которая регистрирует P12 — количество случаев в единицу времени, когда фотоны попадут в фотоумножители одновременно. Пусть aA амплитуда появления фотона, испущенного источником A, в детекторе a, аналогично определим aB, bA и bB. Амплитуда того, что фотоны, испущенные источниками A и B, одновременно окажутся соответственно в детекторах a и b равна aAbB. Покажите, что скорость счета совпадений пропорциональна 2+cos2k(R2-R1), где k — волновое число фотонов, R2 и R1 — расстояния от одного из источников до детекторов. Как использовать этот результат для определения D, если L известно?