Колебания в линейных системах со многими степенями свободы
где D = D2 — D1 = n1 — n2 — расстройка контуров.
Уравнение (7.44) совместно с первым и третьим уравнениями системы (7.43) образует замкнутую систему нелинейных ДУ. Для непосредственного решения эта система достаточно сложна, поэтому будем решать её методом вторичного упрощения укороченных уравнений (методом Хохлова). Для этого следует в полученной системе укороченных уравнений выделить свой малый параметр. Будем считать, что коэффициент связи генераторов достаточно мал, так что
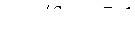 ,
, 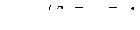 .
.
В этом случае, вторые слагаемые в системе уравнении (7.43), содержащие a1 или a2 малы по сравнению с другими слагаемыми.
Таким образом, будем искать решение системы уравнений (7.43) с помощью разложения в ряд по малому параметру m и ограничиваясь линейными слагаемыми:
|
|
(7.45) |
где A0, B0 — амплитуды колебаний в несвязанных генераторах при m = 0. Из (7.43) и определения m можно просто получить следующие условия: 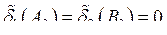 . Тогда можно записать
. Тогда можно записать
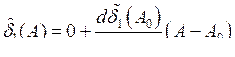 ,
, 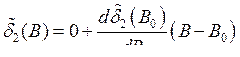 .
.
Отсюда
|
|
(7.46) |
В режиме синхронных колебаний система должна генерировать одну частоту w:
![]() .
.
Эту частоту можно найти из второго и четвёртого уравнения системы (7.43):
|
|
(7.47) |
В синхронном и стационарном режиме разность фаз генераторов F — постоянная величина, тогда из уравнения (7.44) следует, что
|
|
(7.48) |
Подставляя это выражение в формулы (7.45), (7.46) и (7.47), можно найти амплитуду и частоту синхронных колебаний при заданной расстройки контуров D. Естественно, что в (7.48) cos(F) по модулю не должен быть больше единицы, тогда в правой части (7.48) числитель по модулю не может стать больше знаменателя. Поэтому нетрудно видеть, что существует критическая величина расстройки DС, при которой становится невозможным синхронный режим (ширина полосы синхронного режима):
|
|
(7.49) |
Нетрудно видеть, что если один генератор гораздо мощнее другого, то, в соответствии с формулами (7.45) и (7.46), амплитуда более мощного генератора при изменении расстройки почти не меняется. Таким образом, в данном случае мощный генератор затягивает на себя и генерирует частоту близкую к своей парциальной частоте, а маломощный генератор подстраивается под сильного соседа.
Явление затягивания используется для синхронизации генераторов, в частности, в лазерах при синхронизации мод.
Тема 8. Колебания в линейных системах со многими степенями свободы
8.1. Собственные колебания в консервативных системах
Движение в системе с n степенями свободы описывается n независимыми координатами, выбор которых произволен. Число степеней свободы определяется минимальным числом переменных, необходимых для полного описания движения.
Можно также ввести нормальные координаты, число которых равно числу степеней свободы. Движение каждой нормальной координаты происходит независимо от остальных. Поэтому каждая нормальная координата совершает гармоническое колебание с собственной, или нормальной, частотой. Любые свободные и вынужденные колебания можно представить в виде суперпозиции нормальных колебаний.
Для исследования собственных колебаний в системе с n степенями свободы воспользуемся уравнениями Лагранжа. Пусть движение в системе определяется n независимыми обобщёнными координатами q1,…, qn.
Потенциальная энергия системы является функцией обобщённых координат V(q1,…, qn). В положении устойчивого равновесия потенциальная энергия имеет минимум, т. е.
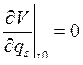 , s = 1,…, n,
, s = 1,…, n,
где qs0 — значение координат в точке равновесия. Если в качестве новых координат выбрать xs = qs — qs0 — отклонения от равновесных значений координат, то для малых xs можно записать
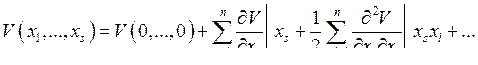
Потенциальная энергия определяется с точностью до постоянной, поэтому положим V(0,…, 0) = 0. Таким образом, пренебрегая высшими степенями в разложении, получим
|
|
(8.1) |
Потенциальная энергия является положительно определённой квадратичной формой отклонения обобщённых координат от положения равновесия, ksl ³ 0, ksl = kls. Аналогично кинетическая энергия системы является положительно определённой квадратичной формой обобщённых скоростей:
|
|
(8.2) |
В уравнениях (8.1) и (8.2) члены с s = l описывают энергию парциальных систем, а члены с s ¹ l соответствуют энергии связи между s-й и l-й парциальными системами.
Для каждой координаты можно записать уравнение Лагранжа (1.30) в виде
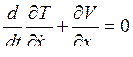 , s = 1,…, n,
, s = 1,…, n,
отсюда получим n линейных ДУ, которые могут быть записаны в матричной форме в виде
|
|
(8.3) |
где матрицы массы ![]() , упругости
, упругости ![]() и вектор обобщённых координат
и вектор обобщённых координат ![]() равны соответственно
равны соответственно
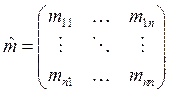 ,
, 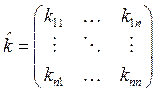 ,
, 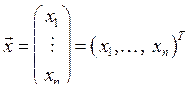 .
.
Решение матричного уравнения (8.3) естественно искать в виде экспоненты
 ,
,
где амплитудный вектор ![]() в общем случае может быть комплексным. Подставляя решение в уравнение, можно записать
в общем случае может быть комплексным. Подставляя решение в уравнение, можно записать
|
|
(8.4) |
Нетривиальное решение матричного уравнения (8.4) возможно лишь при условии равенства нулю определителя системы
|
|
(8.5) |
которое является уравнением n-й степени относительно w2 и имеет n корней ![]() , s = 1,…, n. Так как все коэффициенты уравнения (8.5) — действительные числа, тогда истинное решение на частоте ws следует искать в виде
, s = 1,…, n. Так как все коэффициенты уравнения (8.5) — действительные числа, тогда истинное решение на частоте ws следует искать в виде
|
|
(8.6) |
Амплитудный вектор ![]() должен удовлетворять уравнению вида (8.4):
должен удовлетворять уравнению вида (8.4):
|
|
(8.7) |
Это матричное уравнение эквивалентно системе n однородных уравнений для амплитуд Asm. Первый индекс у амплитуды соответствует номеру собственной частоты, второй индекс — номеру координаты. Опять-таки, чтобы существовало нетривиальное решение, нужно, чтобы определитель последнего соотношения равнялся нулю. Если детерминант равняется нулю, то одну из амплитуд можно выразить через все остальные. Зафиксируем As1, тогда сможем найти все остальные амплитуды, а соответственно и коэффициенты распределения амплитуд:
 , m = 1,…, n, s = 1,…, n.
, m = 1,…, n, s = 1,…, n.
Величины csm при фиксированном s образуют вектор ![]() , который называется вектором коэффициентов распределения амплитуд на частоте ws, а все коэффициенты csm — квадратную матрицу:
, который называется вектором коэффициентов распределения амплитуд на частоте ws, а все коэффициенты csm — квадратную матрицу:
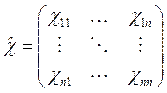 .
.
Амплитудные вектора ![]() и
и ![]() выражаются через
выражаются через ![]() следующим образом:
следующим образом:
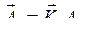 ,
,  .
.
Поэтому, подставляя эти соотношения в (8.6), получим s-е собственное колебание в виде
|
|
(8.8) |
Каждая из функций вида (8.8) является решением (8.3). В силу принципа суперпозиции, общее решение нужно записать в виде взвешенной суммой (8.8):
|
|
(8.9) |
В этом выражении Cs и js определяются начальными условиями, а формы собственных колебаний ![]() и частоты ws зависят от параметров системы.
и частоты ws зависят от параметров системы.
Введём нормальные координаты, т. е. такие координаты, которые совершают гармонические колебания при любых начальных условиях. Их можно ввести следующим образом. Зададим n гармонических колебаний вида
 , s = 1,…, n.
, s = 1,…, n.
Каждое из колебаний hs можно рассматривать как нормальное колебание. Если так выделить нормальные колебания, то движение l-той координаты можно представить как
|
|
(8.10) |
Уравнения (8.10) выражают обобщённые координаты через нормальные. В матричном виде (8.10):
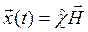 ,
,
где ![]() — вектор, образованный нормальными координатами.
— вектор, образованный нормальными координатами.
Подставим ![]() в таком виде в (8.3), тогда
в таком виде в (8.3), тогда
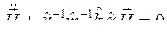 .
.
Так как каждая нормальная координата совершает гармоническое колебание, то для любого hs справедливо равенство
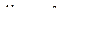 ,
,
поэтому из двух последних соотношений следует:
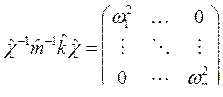 ,
,
т. е. ![]() — диагональная матрица с элементами
— диагональная матрица с элементами ![]() .
.
8.2. Ортогональность нормальных колебаний и экстремальные свойства собственных частот
Каждому нормальному колебанию с частотой ws соответствует определенное распределение амплитуд по координатам, или определённая форма колебаний. Формы колебаний, соответствующие разным собственным частотам, ортогональны друг другу. Для того, чтобы показать это, запишем уравнение (8.3) для s-й и r-й форм колебаний:
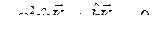 ,
, 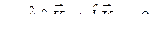 .
.
Умножим скалярно справа первое из этих уравнений на ![]() , а второе на
, а второе на ![]() . Учитывая, что матрицы
. Учитывая, что матрицы ![]() и
и ![]() симметричны, т. е.
симметричны, т. е. 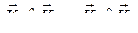 ,
, 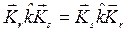 , вычтем из второго уравнения первое:
, вычтем из второго уравнения первое:
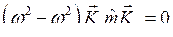 .
.
Если ws ¹ wr, то отсюда
|
|
(8.11) |
С учётом формул (8.3) и (8.11) получаем также
|
|
(8.12) |
Соотношения (8.11) и (8.12) называются условием ортогональности s-й и r-й форм нормальных колебаний. Использование условий ортогональности нормальных колебаний даёт возможность получить некоторые соотношения, общие для любых систем с n степенями свободы. Покажем, например, что потенциальная энергия любого собственного колебания равна сумме потенциальных энергий всех собственных колебаний. Потенциальную энергию системы (8.1) в матричной форме можно записать в виде
 .
.
Подставляя теперь выражение вида (8.10) и учитывая условие ортогональности (8.12), получим
|
|
(8.13) |
Аналогично с учётом условия ортогональности (8.11) легко показать, что
|
|
(8.14) |
Выражения (8.13) и (8.14) показывают, что в нормальных координатах и потенциальная, и кинетическая энергия являются диагональными квадратичными формами. Следовательно, систему с п степенями свободы можно представить как набор из п независимых систем с одной степенью свободы.
Зададим в момент времени t = 0 произвольное отклонение от положения равновесия системы ![]() . Пусть скорости изменения координат в тот же момент времени равны нулю, т. е.
. Пусть скорости изменения координат в тот же момент времени равны нулю, т. е. 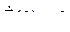 . Тогда из уравнения (8.9) следует, что колебание в системе в любой момент времени t > 0 можно записать в виде
. Тогда из уравнения (8.9) следует, что колебание в системе в любой момент времени t > 0 можно записать в виде
|
|
(8.15) |
Потенциальная и кинетическая энергия системы при этом с учетом формул (8.11) и (8.12) равны
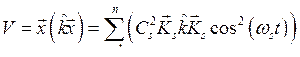 ,
, 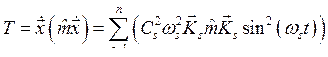 .
.
При колебаниях в консервативной системе среднее по времени значение потенциальной энергии равно среднему значению кинетической энергии, т. е.
|
|
(8.16) |
Расположим собственные частоты в порядке их возрастания:
 .
.
Если заменить все ![]() квадратом наинизшей частоты
квадратом наинизшей частоты ![]() , то (8.16) превращается в неравенство
, то (8.16) превращается в неравенство
|
|
(8.17) |
Левая часть неравенства (8.17) является функцией амплитуд Cs, т. е. функцией начального распределения амплитуд по степеням свободы. Величина ![]() является минимумом левой части (8.17) как функции
является минимумом левой части (8.17) как функции ![]() . Таким образом, используя соотношение (8.15), получим
. Таким образом, используя соотношение (8.15), получим
|
|
(8.18) |
Этот минимум достигается в том случае, когда все Cs, за исключением C1, равны нулю. Тогда ![]() , т. е. распределение амплитуд по координатам совпадает с первой собственной формой колебания. Для нахождения второй собственной частоты w2 следует выбрать начальное отклонение
, т. е. распределение амплитуд по координатам совпадает с первой собственной формой колебания. Для нахождения второй собственной частоты w2 следует выбрать начальное отклонение ![]() ортогональным первой собственной форме колебания, т. е.
ортогональным первой собственной форме колебания, т. е.
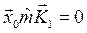 и
и 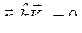 .
.
Тогда в выражении (8.16) суммирование начинается с s = 2 и самой низкой частотой окажется частота w2. Приводя рассуждения, аналогичные изложенным выше, получим
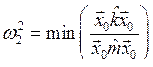 .
.
Минимум этого выражения достигается при  , т. е. когда начальное распределение колебаний совпадает со второй собственной формой. Аналогичным образом можно найти все собственные частоты колебаний ws и собственные формы
, т. е. когда начальное распределение колебаний совпадает со второй собственной формой. Аналогичным образом можно найти все собственные частоты колебаний ws и собственные формы ![]() (по индукции легко показывается, что все квадраты собственных частот являются экстремумами некоторых выражений).
(по индукции легко показывается, что все квадраты собственных частот являются экстремумами некоторых выражений).
8.3. Вынужденные колебания в системе с n степенями свободы
Для линейных систем справедлив принцип суперпозиции колебаний. Поэтому задача о вынужденных колебаниях в системе под действием любой периодической силы сводится к нахождению вынужденных движений системы в результате действия гармонической силы частоты w. Если рассматриваемая система консервативна, то уравнение её колебаний в матричной форме принимает вид:
|
|
(8.19) |
Вынужденные колебания системы должны быть гармоникой той же частоты
|
|
(8.20) |
где ![]() — амплитудный вектор вынужденных колебаний. Подставляя решение (8.20) в (8.19), получим уравнение для амплитудного вектора
— амплитудный вектор вынужденных колебаний. Подставляя решение (8.20) в (8.19), получим уравнение для амплитудного вектора
|
|
(8.21) |
Таким образом, для отыскания выражения для вынужденного колебания в матричной форме необходимо обратить матрицу 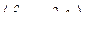 . Отметим, что в силу условия (8.5) в резонансе, т. е. при w = ws, определитель этой матрицы равен нулю, следовательно, обратная матрица обращается в бесконечность.
. Отметим, что в силу условия (8.5) в резонансе, т. е. при w = ws, определитель этой матрицы равен нулю, следовательно, обратная матрица обращается в бесконечность.
 ,
, 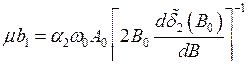 .
.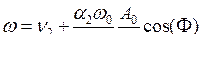 .
. .
.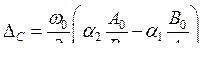 .
.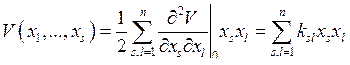 .
.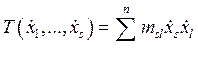 .
.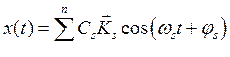 ,
, 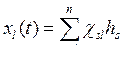 , l = 1,…, n.
, l = 1,…, n.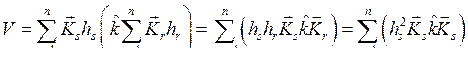 .
. .
.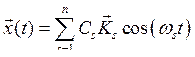 ,
, 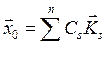 .
.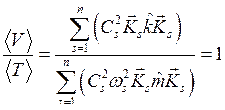 .
.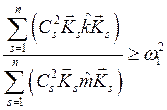 .
.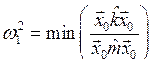 .
.

