Кручение
где ![]() – допускаемое касательное напряжение при сдвиге (
– допускаемое касательное напряжение при сдвиге (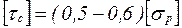 – для пластичных материалов и
– для пластичных материалов и 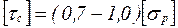 – для хрупких материалов).
– для хрупких материалов).
Расчёту на прочность при сдвиге подлежат сварные швы, заклёпки, болты и другие виды соединения, работающие на сдвиг (срез).
Пример 5.1. Определить минимальную высоту головки (рис. 24) болта из условия равнопрочности её со стержнем.
Решение. При малой высоте h головки болта происходит её срез по цилиндрической поверхности диаметром d. Сила F, растягивающая стержень болта, будет перерезывающей для головки (F=Q) . Полагаем, что касательные напряжения постоянны по высоте h:
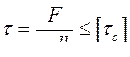 .
.
При этом растягивающие напряжения в стержне болта
![]()
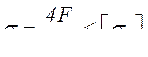 .
.
Откуда, обращая неравенства в равенства, будем иметь
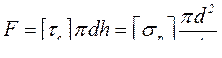 , тогда
, тогда 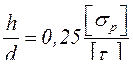 .
.
Принимая для пластичных материалов 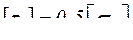 , найдём
, найдём 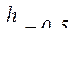 .
.
Таким образом, условие равнопрочности головки болта с его стержнем будет соблюдено при высоте головки болта равной половине диаметра стержня болта.
5.2. Кручение
Кручением называется такой вид деформации стержня (вала), при котором в поперечных сечениях возникает только крутящий момент.
5.2.1. Определение крутящего момента
Для определения крутящего момента в каком-либо сечении используют метод сечений.
Рассмотрим пример, показанный на рис. 25а. Здесь к четырём шкивам, сидящим жёстко на валу, приложены внешние скручивающие вал моменты 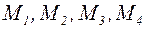 разной направленности. Для определения крутящего момента в сечении z рассмотрим равновесие, например, левой части (рис. 25б), для которой уравнение равновесия имеет вид:
разной направленности. Для определения крутящего момента в сечении z рассмотрим равновесие, например, левой части (рис. 25б), для которой уравнение равновесия имеет вид:
![]() , откуда
, откуда 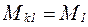 .
.
![]() При определении крутящих моментов придерживаются правила знаков: если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит крутящий момент Мк направленным против часовой стрелки, то момент считается положительным.
При определении крутящих моментов придерживаются правила знаков: если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит крутящий момент Мк направленным против часовой стрелки, то момент считается положительным.
В любом сечении вала действует крутящий момент, равный сумме внешних моментов, находящихся по одну сторону этого сечения. Делая поочерёдно аналогичные сечения вала на участках между шкивами
(рис. 25а), находим значении ![]() . Распределение крутящего момента по длине вала изображается в виде эпюры, показанной на рис. 25в.
. Распределение крутящего момента по длине вала изображается в виде эпюры, показанной на рис. 25в.
5.2.2. Перемещения при кручении
Опыт показывает, что при кручении круглых валов:
– плоские поперечные сечения до деформации остаются плоскими и после приложения нагрузок, сами сечения при этом не искажаются;
– расстояние между любыми двумя поперечными сечениями не меняется;
– все образующие поверхности вала (линии, параллельные его оси) поворачиваются на один и тот же угол.
Деформация вала при кручении происходит за счёт сдвига одного сечения относительно другого из-за касательных напряжений τ, действующих в сечении (рис. 26). Для выяснения закона изменения деформации по сечению вырежем из вала двумя поперечными сечениями элемент длиной dz, условно закрепив жёстко один из его торцов (сечение I−I). В результате действия крутящего момента ![]() сечение II−II повернётся относительно условно закреплённого сечения I−I на угол
сечение II−II повернётся относительно условно закреплённого сечения I−I на угол ![]() . Точка В переместится в положение В1. Угол
. Точка В переместится в положение В1. Угол ![]() между новым положением образующей АВ1 и первоначальным АВ называется относительным углом сдвига или относительным сдвигом.
между новым положением образующей АВ1 и первоначальным АВ называется относительным углом сдвига или относительным сдвигом.
 Из рис. 26 видно, что
Из рис. 26 видно, что
![]() ,
,
откуда находим
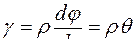 . (5.8)
. (5.8)
Отношение ![]() представляет угол закручивания на единицу длины вала, обозначается θ и называется относительным углом закручивания. Здесь ρ – текущий радиус-вектор.
представляет угол закручивания на единицу длины вала, обозначается θ и называется относительным углом закручивания. Здесь ρ – текущий радиус-вектор.
Подставляя значение γ (5.8) в формулу (5.4) закона Гука при сдвиге, получим
![]() . (5.9)
. (5.9)
Полученное выражение определяет закон распределения касательного напряжения по сечению. Поскольку в сечении 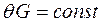 , то напряжения изменяются пропорционально радиусу ρ. Из (5.9) следует, что на контуре сечения касательные напряжения принимают максимальные значения.
, то напряжения изменяются пропорционально радиусу ρ. Из (5.9) следует, что на контуре сечения касательные напряжения принимают максимальные значения.
Крутящий момент ![]() является результирующим моментом внутренних сил
является результирующим моментом внутренних сил 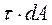 (рис.27) относительно оси z:
(рис.27) относительно оси z:
![]()
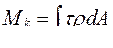 . (5.10)
. (5.10)
Подставляя (5.9) в (5.10), получим
![]() .
.
Поскольку ![]() , то
, то 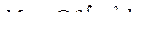 , или
, или
![]() , (5.11)
, (5.11)
где ![]() – полярный момент инерции сечения.
– полярный момент инерции сечения.
Из (5.11) получаем формулу для определения относительного угла закручивания вала:
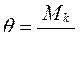 , (5.12)
, (5.12)
тогда угол закручивания
![]()
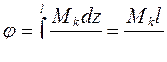 . (5.13)
. (5.13)
Если ![]() ,
, ![]() и l различны на разных участках вала, то в общем случае полный угол закручивания вала можно определить как сумму углов закручивания вала отдельных его участков:
и l различны на разных участках вала, то в общем случае полный угол закручивания вала можно определить как сумму углов закручивания вала отдельных его участков:


