Взаимодействие землеройно-транспортной машины с жёстким тяжёлым препятствием

В формулах (11.2) и (11.3) обозначено:

n – количество деталей, вращающихся при движении агрегата; Jz – момент инерции детали относительно собственной оси вращения; m – масса поступательно движущегося агрегата; rк – радиус ведущей звёздочки или колеса; i – передаточное отношение от центра приведения до приводимого участка.

Основная литература [2, с.117…120]

Дополнительная литература [13, с. 82…84]

Контрольные вопросы:

1.  Приведите характеристику нагрузок, действующих на ЗТМ в условиях эксплуатации.

2.  Из какого равенства можно найти приведенную жёсткость, учитывающую жёсткость препятствия и металлоконструкции бульдозера?

3.  Напишите выражение суммарной приведенной массы агрегата, полученное при приведении его масс к поступательно движущейся массе.

Лекция 12

Взаимодействие землеройно-транспортной машины с жёстким тяжёлым препятствием

При встрече рабочего органа ЗТМ с тяжёлым твёрдым препятствием в результате перегрузки двигателя скорость машины может довольно быстро снизиться до полной остановки (стопорения).

Динамические нагрузки в элементах трансмиссии привода хода, например, бульдозера могут быть определены с помощью упрощённых двухмассных расчётных схем (12.1,а), где c1 – суммарная жёсткость препятствия cпр и рабочего оборудования cр. о; c2 – суммарная приведённая жёсткость элементов трансмиссии; m1 – масса рабочего оборудования и трактора; m2 – суммарная приведенная масса вращающихся элементов двигателя, маховика, трансмиссии и движителей трактора; R – сопротивление передвижению машины до встречи с препятствием; Pд(t) – приведенное движущее усилие двигателя.

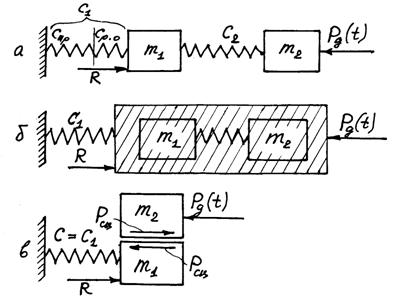
Рисунок 12.1 — Расчётные схемы ЗТМ при стопорении: а – для расчёта нагрузок в элементах трансмиссии; δ – для расчёта нагрузок на рабочее оборудование при неограниченном запасе сцепления движителя с грунтом;

в – для расчёта нагрузок на рабочее оборудование при буксовании движителя.

Данная схема получена приведением всех масс к поступательно движущимся массам, а жёсткостей – к линейной жёсткости.

Расчётные схемы могут быть упрощены до вида, показанного на рис.12,б или рис.12,в. На этих схемах c1 – суммарная приведенная жёсткость рабочего оборудования и препятствия.

В схеме, приведенной на рис.12.1,а под величиной cпр понимается жёсткость массива грунта при резком заглублении рабочего органа. В расчётной схеме (см. рис.12,б) под массой mп понимают сумму поступательно движущихся масс машины и приведённых масс двигателя, маховика и т. д. В третьем случае (см. рис.12,в) масса mп разделена на две части m1 и m2, находящиеся по разные стороны фрикционной связи движителей с грунтом.

Экспериментально установлено, что основная часть процесса взаимодействия рабочего оборудования бульдозера с препятствиями происходит на режиме полного буксования, когда ускорения достигают максимальной величины, скорость падает до нуля и происходит основная часть деформации металлоконструкции и препятствия.

На первом этапе принимают ускорение в начальный момент буксования jmax 0, а скорость vнач.. Тогда максимальное ускорение, возникающее в момент остановки,

jmax — vнач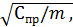 (12.1)

где cпр – приведённая жёсткость; m – масса бульдозера.

Динамическая нагрузка на рабочий орган бульдозера

Pдин= mjmax= vнач (12.2)

а результирующая нагрузка на рабочий орган

Pр. о= Тφ – Ро + Рдин, (12.3)

где Тφ – сила сцепления; Ро – начальное сопротивление движению машины.

Очевидно, к снижению динамических нагрузок, возникающих под действием случайных нагрузок, приводит уменьшение жёсткости навесного оборудования ЗТМ. Снижение жёсткости металлических конструкций рабочего оборудования может быть осуществлено путём введения специальных упругих элементов: пружин, торсионов и др.

Жёсткость упругого элемента можно определить по зависимости:

cу. э= c·cмк/(cмк- c), (12.4)

где c – общая приведенная жёсткость металлоконструкции с упругим элементом; cмк – жёсткость металлоконструкции.

Основная литература [2, с.121…129]

Дополнительная литература [13, с. 85…88]

Контрольные вопросы:

1.  С какой целью составляют упрощённые расчётные схемы ЗТМ при стопорении?

2.  Напишите формулу для определения динамической нагрузки на рабочий орган бульдозера при буксовании.

3.  От каких параметров зависит жёсткость упругого элемента, вводимого в конструкцию рабочего оборудования ЗТМ?

Лекция 13

Уравнение движения трактора и автомобиля

Выясним, какие силы и моменты действуют на трактор (автомобиль), выделим из них силы движения и сопротивления: сила тяжести G (вес) машины, приложенная в центре тяжести и направленная вертикально вниз; ведущий крутящий момент Мвед, подводимый от двигателя, установленного на машине, к оси ведущих колёс; момент сопротивления качению ведомых колёс Мfвм; момент сопротивления качению ведущих колёс Мfвщ; сила сопротивления перекатыванию Pf машины, параллельная направлению движения; касательная сила тяги Ркφ ведущих колёс машины; нагрузка Ркр на крюке, которая изменяется в зависимости от скорости движения и других факторов.

Уравнение движения трактора (автомобиля) напишем в форме Лагранжа:

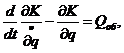
где t – время; К – кинетическая энергия машины, движущейся со скоростью v; q – обобщённая координата; Qоб — обобщённая сила; Qоб = δА/δх.

Здесь δА – сумма работ всех заданных сил и моментов; δх – возможное перемещение.

Кинетическая энергия машины

К = mv2/2+Jпр ·ωk2/2,

где m – масса поступательно движущихся частей машины; Jпр – приведенный к оси ведущих колёс момент инерции вращающихся масс двигателя и трансмиссии; ωk – угловая скорость вращения ведущих колёс.

Значение Jпр можно определить по формуле

Jпр=Jд ·iтр2 ·ηтр+Σ Jх · iх2 · ηх+Jk (13.1)

где Jg, Σ Jх и Jk — моменты инерции вращающихся масс соответственно трансмиссии и от рассматриваемых шестерён до оси ведущих колёс; ηтр и ηх — КПД данных передач.

Здесь iтр = ωд/ ωk, ix = ωx/ ωk; ωд и ωх – угловые скорости вращения соответственно коленчатого вала двигателя и шестерён трансмиссии.

На рис.13.1 условно показаны вращающиеся массы двигателя и трансмиссии машины, обозначены их моменты инерции и угловые скорости вращения.

Так как q = x, т. е. это перемещение машины по оси х, а ωk= v/rk, то .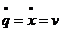

Здесь rк – радиус ведущего колеса.

K= mv2/2 + Jпр · v2/(2rk2) = (mv2/2)[1+ Jпр/m rk2)] = δвр · mv2/2,

ðk/ðx=0,

где δвр – коэффициент учёта вращающихся масс:

δвр=1+ Jпр/(m rk2)1,05…1,25.

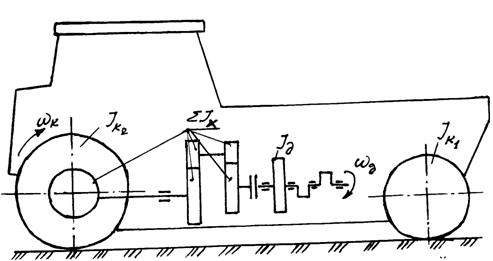
Рисунок 13.1 — Динамическая схема вращающихся частей трактора (автомобиля)

Подставив эти выражения в уравнение (13.1), получим

[(δвр·mv2/2)] = Qоб или δвр·mdv/dt = Qоб . (13.2)

Дифференциальное уравнение движения трактора (автомобиля) в общем виде получим после соответствующих подстановок в уравнения (13.2)

δвр·m = Pkφ – Pсопр или 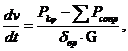(13.3)

где =Pf + Pкр ·cosγкр+ Pω+ G ·sinα – сумма сил сопротивления движению машин.

Здесь Pf, Pкр, Pω, G – силы соответственно перекатыванию, сопротивления воздуха, на крюке, тяжести машины; α – угол подъема дороги; γкр – угол наклона силы на крюке Pкр к горизонтали.

Из уравнения движения (13.3) получим выражение для тягового баланса машины – соотношения движущих сил и сил сопротивления движению

Pkφ = Σ Pсопр ± δвр ·Pj, (13.4)

где Pj = mj – сила инерции поступательно движущихся масс; j = dv/dt – ускорение поступательно движущихся масс машины.

Основная литература [6, с. 309…311]

Дополнительная литература [13, с.17…20]

Контрольные вопросы:

1.  От каких параметров зависит приведенный к оси ведущих колёс момент инерции вращающихся масс двигателя и трансмиссии трактора (автомобиля)?

2.  Напишите выражение дифференциального уравнения движения трактора (автомобиля) в общем виде.