Лекции по квантовой физике
Квантовая физика
Квантовые и волновые свойства вещества. Введение.
Все вещества состоят из атомов и молекул – известная фраза, которую можно найти в любом учебнике, ставшая афоризмом.
Атом (от греческого atomos – неделимый) – наименьшая часть химического элемента, являющаяся носителем его свойств.
Заслуга введения в теорию вещества идеи атомов принадлежит греческим философам (Демокрит, Эпикур). Нелегко понять, что подразумевали древние под термином «атом», но основной проблемой, интересовавшей их, был вопрос о том, бесконечна ли делимость вещества. Греческие атомисты верили, что любое вещество построено из «атомов» и, вероятно, чувствовали, что бесконечное многообразие свойств вещества должно быть объяснено конфигурацией и движением «атомов». Эти идеи довольно близки современным, но различия между нашими количественными теориями, основанными на опыте, и туманными размышлениями древних столь же огромны, как и отличие их «атомов» от того понимания, которое вкладываем в этот термин мы.
Постепенно само существование атомов и молекул, которое долгое время рассматривалось только как удобная рабочая гипотеза, было осознано как объективная реальность. В начале XIX в. в результате установления основных химических законов и законов идеального газа сложились представления об атоме как о мельчайшей частице химического элемента (англ. Дж. Дальтон, итал. А. Авогадро, швед Я. Берцелиус). В середине XIX в. была проведена четкая граница между атомом и молекулой (итал. С. Канниццаро). Важнейшее значение имело открытие в 1869 г. Д. И. Менделеевым периодической системы элементов.
Великие открытия конца XIX в. – рентгеновских лучей (1895 г.), радиоактивности (1896 г, франц. А. Беккерель), электрона (1897 г, англ. Дж. Дж. Томсон); результаты изучения радиоактивности (франц. П. и М. Кюри) окончательно разрушили представление о неизменности и неделимости атома. Стало очевидным, что атом имеет сложное строение.
I. Экспериментальное обоснование современных представлений о структуре атомов.
В 1903 г. Дж. Дж. Томсон предложил модель, согласно которой атом представляет собой положительно заряженную сферу (или равномерно заряженный шар), внутрь которой вкраплены электроны. Суммарный положительный заряд сферы равен заряду электронов, т. е. атом в целом нейтрален.
Испускание света таким атомом – это следствие колебания электронов около положения равновесия.
Первую попытку изучения строения атома на опытах по рассеянию пучков заряженных частиц предпринял Ленард с сотрудниками, используя катодные лучи – пучки электронов с энергией более 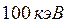 .
.
Оказалось, что быстрые электроны почти совершенно не тормозятся атомом, хотя в результате столкновений с массивными шариками катодное излучение очень скоро неизбежно остановилось бы.
1.Опыт Резерфорда. Ядерная модель атома.
В 1911 г. Э. Резерфорд поставил опыты по изучению рассеяния ![]() частиц при прохождении через тонкие металлические фольги. Резерфорд выбрал для своих экспериментов значительно более массивные
частиц при прохождении через тонкие металлические фольги. Резерфорд выбрал для своих экспериментов значительно более массивные ![]() частицы, а не сравнительно легкие электроны, в силу того, что
частицы, а не сравнительно легкие электроны, в силу того, что ![]() частицы не отклоняются сколько-нибудь заметным образом при столкновениях с электронами атома и поэтому будут реагировать только на столкновения с более тяжелыми частицами. Разница в проникающих способностях электрона и
частицы не отклоняются сколько-нибудь заметным образом при столкновениях с электронами атома и поэтому будут реагировать только на столкновения с более тяжелыми частицами. Разница в проникающих способностях электрона и ![]() частицы сравнима с разницей между легкой ружейной пулей и тяжелым снарядом.
частицы сравнима с разницей между легкой ружейной пулей и тяжелым снарядом. ![]() частицы испускались в результате радиоактивного распада и имели скорость порядка
частицы испускались в результате радиоактивного распада и имели скорость порядка 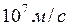 .
.
Узкий пучок ![]() частиц направлялся на мишень (Ф)
частиц направлялся на мишень (Ф)
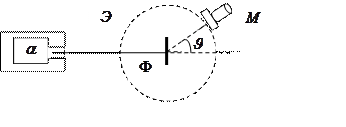 из тонкой фольги. Рассеянные
из тонкой фольги. Рассеянные ![]() частицы
частицы
регистрировались визуально – удар ![]() частицы об
частицы об
экран (Э) из сернистого цинка, окружавший
мишень, вызывал сцинтилляцию (вспышку света),
наблюдаемую в микроскоп (М). Весь прибор
помещался в вакуумированную оболочку.
Подавляющее число ![]() -частиц рассеивалось на малые углы
-частиц рассеивалось на малые углы 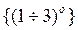 , однако некоторое количество
, однако некоторое количество
![]() -частиц отклонялось на очень большие углы (до
-частиц отклонялось на очень большие углы (до![]() ). Например, на платиновой фольге из
). Например, на платиновой фольге из ![]()
 падающих
падающих ![]() -частиц
-частиц ![]() (одна) рассеивалась на угол больше
(одна) рассеивалась на угол больше ![]() .
.
Анализируя результаты опыта, Резерфорд пришел
к выводу, что столь сильное отклонение ![]() -частиц
-частиц
вызывается чрезвычайно сильным электрическим полем,
которое создается зарядом, связанным с большой массой
и сконцентрированным в очень малом объеме. Остальное
внутриатомное пространство практически ничем не заполнено – результат, уже полученный ранее Ленардом. Поскольку ![]() частицы, по Резерфорду, заметно отклоняются лишь ядром, можно вывести закон рассеяния из распределения
частицы, по Резерфорду, заметно отклоняются лишь ядром, можно вывести закон рассеяния из распределения ![]() частиц, отклоненных тонкой пленкой изучаемого образца. Таким путем получается совершенно недвусмысленный вывод – эффективная рассеивающая сила представляет собой кулоновскую силу
частиц, отклоненных тонкой пленкой изучаемого образца. Таким путем получается совершенно недвусмысленный вывод – эффективная рассеивающая сила представляет собой кулоновскую силу ![]() , где
, где ![]() заряд
заряд ![]() частицы, а
частицы, а ![]() заряд ядра. Траектории
заряд ядра. Траектории ![]() частиц имеют вид гипербол, в фокусе которых расположено ядро.
частиц имеют вид гипербол, в фокусе которых расположено ядро.
В отличие от Томсона, который отклонение на большие углы пытался объяснить множественными актами рассеяния, Резерфорд объяснил этот эффект однократным актом рассеяния и получил согласие с экспериментом. ![]()
Исходя из кулоновского характера взаимодействия и известной скорости налетающих ![]() -частиц, можно (в нерелятивистском приближении) оценить размер области, в которой сконцентрирован рассеивающий положительный заряд. Определим его как расстояние, на которое подошла бы летящая точно по направлению к ядру и отброшенная в обратном направлении
-частиц, можно (в нерелятивистском приближении) оценить размер области, в которой сконцентрирован рассеивающий положительный заряд. Определим его как расстояние, на которое подошла бы летящая точно по направлению к ядру и отброшенная в обратном направлении ![]() -частица.
-частица.
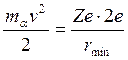 , пусть
, пусть 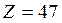 (серебро),
(серебро), 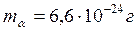 ,
, 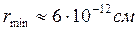 .
.
Т. о., ядро обладает конечными размерами.
Для почти центральных столкновений, т. е. рассеяния на большие углы, наблюдается отклонение распределения рассеянных частиц от формулы, полученной на основе закона Кулона. Отсюда следует вывод, что закон Кулона перестает быть справедливым на расстояниях около 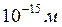 (или, иначе, выполняется на расстояниях, больших
(или, иначе, выполняется на расстояниях, больших ![]() ).
).
Т. о., согласно Резерфорду (1911 г.), атом можно представить себе следующим образом. В центре атома находится ядро с зарядом ![]() , имеющее размер, не более
, имеющее размер, не более 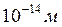 . Вокруг ядра распределены
. Вокруг ядра распределены ![]() электронов, в области размером порядка
электронов, в области размером порядка ![]() . Масса атома сосредоточена, в основном, в ядре.
. Масса атома сосредоточена, в основном, в ядре.
Проиллюстрировать масштабы и заполненность внутриатомного пространства можно на следующем примере. Если увеличить каплю воды до размеров земного шара и все атомы в ней в той же пропорции, то диаметр атома достигнет нескольких метров, а диаметр ядра составит лишь 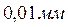 .
.
Замечания.
1. Планетарная модель была впервые предложена в лекции Перрена (J. Perrin) в Сорбонне в 1901 г.: положительно заряженная частица, окруженная некоторым числом электронов («наподобие маленьких планет»), компенсирующих заряд центральной частицы. Перрен предполагал, что под действием внутренних электромагнитных сил образуется динамически устойчивая система, периоды вращения в которой соответствуют частотам (длинам волн) линий спектра атома.
2. «Опыт Резерфорда» был поставлен Гейгером и Мёрсденом [H. Geiger, E. Mursden. On a diffuse reflection of the ![]() particles. Proc. Roy. Soc. London (A), v.82,1909; есть также статья 1910г.]
particles. Proc. Roy. Soc. London (A), v.82,1909; есть также статья 1910г.]
3. В 1911 г. Резерфордом опубликована статья [The scattering of ![]() and
and ![]() particles by matter and structure of the atom,- Phyl. Mag., v.21,1911], содержавшая формулу рассеяния и обоснование планетарной (ядерной) модели атома.
particles by matter and structure of the atom,- Phyl. Mag., v.21,1911], содержавшая формулу рассеяния и обоснование планетарной (ядерной) модели атома.
4. Отклонение ![]() частиц на большие углы, наблюдавшееся в опытах Гейгера и Мёрсдена, Томсон пытался объяснить множественными актами рассеяния, что дает
частиц на большие углы, наблюдавшееся в опытах Гейгера и Мёрсдена, Томсон пытался объяснить множественными актами рассеяния, что дает 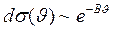 ,
, 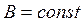 . Резерфорд же, объясняя этот результат однократным актом рассеяния, получил в согласии с экспериментом
. Резерфорд же, объясняя этот результат однократным актом рассеяния, получил в согласии с экспериментом 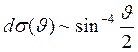 . Кроме того, как выяснилось позже, модель Томсона не объясняет эффекта Штарка, не допускает эффекта Зеемана и т. д.
. Кроме того, как выяснилось позже, модель Томсона не объясняет эффекта Штарка, не допускает эффекта Зеемана и т. д.
Резерфорду мы обязаны, прежде всего, нашими конкретными количественными представлениями о строении атома.
Рассеяние частиц в атомной физике (физике элементарных частиц) принято описывать эффективным сечением. Эффективное сечение (![]() ) – величина, характеризующая вероятность перехода системы двух сталкивающихся частиц в результате их рассеяния (упругого или неупругого) в определенное конечное состояние. Упругое рассеяние частиц характеризуют дифференциальным эффективным сечением
) – величина, характеризующая вероятность перехода системы двух сталкивающихся частиц в результате их рассеяния (упругого или неупругого) в определенное конечное состояние. Упругое рассеяние частиц характеризуют дифференциальным эффективным сечением ![]() , равным отношению числа частиц, упруго рассеянных в единицу времени в единичный телесный угол (
, равным отношению числа частиц, упруго рассеянных в единицу времени в единичный телесный угол (![]() элемент телесного угла), к потоку падающих частиц; а также полным эффективным сечением , равным интегралу дифференциального сечения, взятому по полному телесному углу
элемент телесного угла), к потоку падающих частиц; а также полным эффективным сечением , равным интегралу дифференциального сечения, взятому по полному телесному углу ![]() стерадиан. Эффективное сечение всецело определяется видом рассеивающего поля и является важнейшей характеристикой процесса рассеяния; имеет размерность площади.
стерадиан. Эффективное сечение всецело определяется видом рассеивающего поля и является важнейшей характеристикой процесса рассеяния; имеет размерность площади.
Т. о., следуя Резерфорду, получим выражение, связывающее эффективное сечение с углами рассеяния частиц. Определим эффективное сечение ![]() как отношение числа
как отношение числа ![]() частиц, рассеиваемых в единицу времени на углы от
частиц, рассеиваемых в единицу времени на углы от ![]() до
до 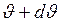 , к плотности потока
, к плотности потока ![]() (интенсивности
(интенсивности 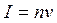 ) рассеиваемых частиц, т. е. к числу частиц, проходящих в единицу времени через единичную площадку, перпендикулярную их скорости
) рассеиваемых частиц, т. е. к числу частиц, проходящих в единицу времени через единичную площадку, перпендикулярную их скорости ![]()
 (
(![]() — концентрация частиц в пучке):
— концентрация частиц в пучке):
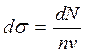 .
.
Классическое решение задачи о рассеянии
заряженной частицы на массивном точечном
заряде было получено в механике (задача 2х тел),
чем мы и воспользуемся.
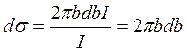 .
.
Для ![]() частицы (
частицы (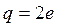 ) связь между прицельным параметром
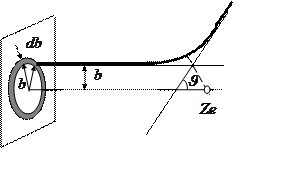
) связь между прицельным параметром ![]() (длина перпендикуляра, опущенного из рассеивающего центра, на направление касательной к траектории находившейся на бесконечности частицы) и углом рассеяния:
(длина перпендикуляра, опущенного из рассеивающего центра, на направление касательной к траектории находившейся на бесконечности частицы) и углом рассеяния:
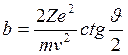 , или
, или 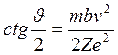 . (*)
. (*)
Поскольку в классике между параметрами ![]() и
и ![]() существует однозначная связь, то число частиц, рассеянных на углы
существует однозначная связь, то число частиц, рассеянных на углы 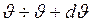 (в телесный угол
(в телесный угол 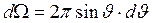 ), определяется числом частиц, прошедших через площадку
), определяется числом частиц, прошедших через площадку ![]() , т. е.
, т. е.
Выразим дифференциал прицельного параметра ![]() , продифференцировав выражение (*):
, продифференцировав выражение (*):
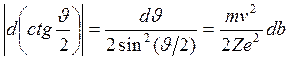
![]()
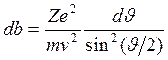 ,
,
откуда
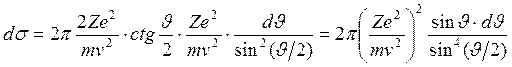 ,
,
учитывая, что ![]() , получаем для дифференциального сечения рассеяния:
, получаем для дифференциального сечения рассеяния:


