Метод эквивалентного генератора
9.4.3. Пусть узловое напряжение ![]() направлено от узла k к узлу d, токи в активных ветвях направлены по направлению ЭДС, ток в пассивной ветви
направлено от узла k к узлу d, токи в активных ветвях направлены по направлению ЭДС, ток в пассивной ветви ![]() – по направлению
– по направлению ![]() (см. рис. 9.17).
(см. рис. 9.17).
9.4.4. Определяем проводимость ветвей схемы рис. 9.17:
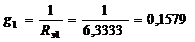 См,
См,
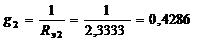 См,
См,
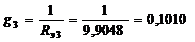 См.
См.
9.4.5. Вычисляем узловое напряжение ![]() по формуле
по формуле
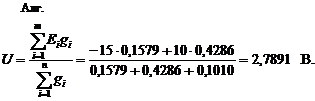
при этом первое слагаемое в числителе записываем со знаком “–”, так как ток ![]() имеет направление, согласное с принятым направлением
имеет направление, согласное с принятым направлением ![]() .
.
9.4.6. Составляем уравнение в соответствии со II законом Кирхгофа для каждой ветви схемы (рис. 28) в отдельности и вычисляем значения токов ![]() ,
, ![]() ,
, ![]() :
:
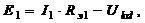
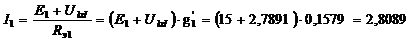 А,
А,
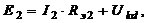
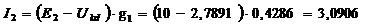 А,
А,
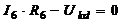 B,
B,
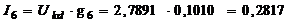 А.
А.
34
9.4.7. Выполним проверку решения в соответствии с I законом Кирхгофа для узла k:
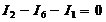 ,
,
3,0906 – 0,2817 – 2,8089 = 0.
9.4.8. Расчет токов ![]() ,
, ![]() ,
, ![]() в схеме (рис. 9.2) должен быть выполнен также, как показано в п. п. 9.3.7., 9.3.8., 9.3.9.
в схеме (рис. 9.2) должен быть выполнен также, как показано в п. п. 9.3.7., 9.3.8., 9.3.9.
9.5 Метод эквивалентного генератора
9.5. Расчет тока в цепи источника ![]() (через резистор
(через резистор ![]() ) методом эквивалентного генератора.
) методом эквивалентного генератора.
9.5.1. Заменим исходную схему (рис. 9.1) схемой эквивалентного генератора (рис. 9.18), где ток ![]() находится по формуле согласно закону Ома:
находится по формуле согласно закону Ома:
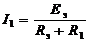 ,
,
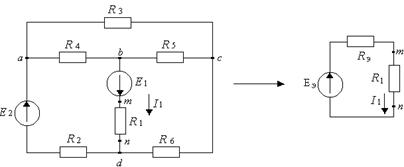
Рисунок 9.18
Так как схемы на рис 9.18 эквивалентны, напряжение холостого хода с зажимов ![]()
![]()
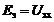 будем искать, создав режим холостого хода в исходной схеме между точками m и n (рис. 9.19).
будем искать, создав режим холостого хода в исходной схеме между точками m и n (рис. 9.19).
35
Рисунок 9.19
9.5.2. Выбираем произвольно направление напряжения холостого хода ![]() и токов, определяем направления токов в цепи (см. рис 9.19)
и токов, определяем направления токов в цепи (см. рис 9.19) ![]() , как токов в простой цепи, направления которых определяются полярностью источника ЭДС
, как токов в простой цепи, направления которых определяются полярностью источника ЭДС ![]() , и составляем уравнения в соответствии со ІІ законом Кирхгофа для контура abmnd , обходя его по часовой стрелке, как это показано на рис 9.19:
, и составляем уравнения в соответствии со ІІ законом Кирхгофа для контура abmnd , обходя его по часовой стрелке, как это показано на рис 9.19:
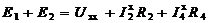 (1)
(1)
9.5.3. Для расчета значений ![]() и
и ![]() удалим из схемы ветвь вd (в ней отсутствует ток) (рис. 9.20) и произведем расчет образовавшейся простой цепи методом “свертывания” (рис. 9.21, 9.22, 9.23):
удалим из схемы ветвь вd (в ней отсутствует ток) (рис. 9.20) и произведем расчет образовавшейся простой цепи методом “свертывания” (рис. 9.21, 9.22, 9.23):
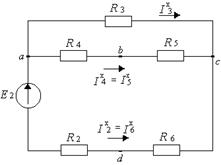
Рисунок 9.20
36
а) прямой ход
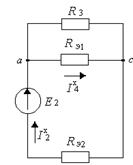
Рисунок 9.21
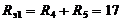 Ом,
Ом,
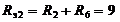 Ом;
Ом;
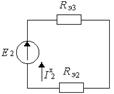
Рисунок 9.22
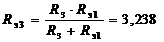 Ом;
Ом;
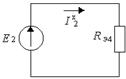
Рисунок 9.23
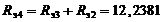 Ом;
Ом;
37
б) обратный ход
рис. 9.24: ![]() А,
А,


