Метод спектра инвариантных масс

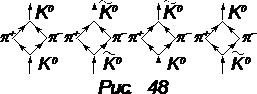Обратимся к идее виртуальных состояний. Допустим, имеется нейтральный каон, находящийся в нераспавшемся состоянии. Виртуально он может находиться в распадном состоянии. Так как виртуальный распад — это не совершившийся распад, каон может вернуться в исходное состояние ÷K0ñ®÷p+p—ñ®÷K0ñ. Возможно виртуальное колебание состояния каона. Такое же колебание может испытывать анти-ка-ноль-мезон ÷0ñ®÷p+p—ñ ®÷0ñ. В квантовой механике справедлив закон, который говорит, “то, что произойдет с состоянием в последующие моменты времени, целиком определяется состоянием в данный момент времени, и не зависит от того, как система попала в данное состояние”. Нейтральный каон, находящийся в виртуальном состоянии, может с равным успехом оказаться и в состоянии анти-ка-ноль-мезона (см. фейнмановские диаграммы виртуальных распадов на рисунке 48). Этот вывод справедлив для обоих каонов. Из данных рассуждений следует, что состояния ÷K0ñ и ÷0ñ связаны. Действительна аналогия с маятниками. Состояние ÷K0ñ аналогично состоянию |колеблется левый маятникñ, а ÷0ñ — состоянию |колеблется правый маятникñ. Так как состояния связаны, должны наблюдаться биения. Каон должен превращаться в антикаон, и наоборот. Время превращения нейтрального каона в свою античастицу определяется величиной связи. Это явление теоретически предсказали Гел-Манн и Нишиджима. Они предложили экспериментаторам провести такой эксперимент. Пучок нейтральных каонов направить в длинную трубу, заполненную водородом в газовой фазе, чтобы каон мог пролетать большое расстояние без столкновений. При влете, поскольку он находится в чистом состоянии ÷K0ñ, при редких столкновениях с протонами ни в коем случае невозможны образования лямбда-ноль. Но через некоторое время, равное половине периода биений, пролетев соответствующее расстояние, нейтральный каон превращается в свою античастицу, и при столкновениях теперь возможно образование лямбда-ноль. Постановка эксперимента подтвердила это предсказание.

3. Домашнее задание

3.2 Решение задач

Задача 1. Состояния ÷K0ñ и ÷0ñ со временем переходят друг в друга, аналогично биениям в системе связанных маятников. Продолжая аналогию, можно предположить, что равные смеси состояний (÷K0ñ+÷0ñ)/ и (÷K0ñ-÷0ñ)/ должны быть аналогичны модам колебаний маятников с определенными частотами, т. е. они должны быть состояниями с определенным значением энергии. Экспериментальные исследования подтверждают это предположение. Оказалось, что разность энергий состояний ÷KSñ=(÷K0ñ+÷0ñ)/ (симметричный каон) и ÷KАñ=(÷K0ñ-÷0ñ)/ (антисимметричный каон) равна всего 3,4×10-3 эВ. Используя этот экспериментальный факт, определите, на каком расстоянии от начала трубы с газообразным водородом, в которую направляется пучок нейтральных каонов, можно с наибольшей вероятностью ожидать рождение лямбда-ноль частиц, если кинетическая энергия влетающих каонов равна 1000×mKc2.

занятие 2.3.5

Адронное взаимодействие. резонансы

2. Метод спектра инвариантных масс

2.1 Спектральный состав зависимости амплитуды вероятности распадающегося состояния от времени

Один из широко распространенных методов измерения средних времен жизни элементарных частиц состоит в расшифровке треков, оставляемых в пузырьковой, туманной или эмульсионной камерах. Среднее время жизни частицы находится из измерений длин пробега между рождением и распадом. При временах жизни порядка t~10-12 с частица между рождением и распадом проходит расстояние порядка ct. За счет увеличения времени жизни в лабораторной системе отсчета эти расстояния могут составлять от долей миллиметра до метров. Частицы, распадающиеся в результате электромагнитного взаимодействия, как, например, нейтральный пион (t~10-16 с), только при скоростях, очень близких к скорости света могут оставить след заметной длины. Примеры рассмотрения скоростей взаимодействий на предыдущем занятии показали, что времена жизни частиц относительно адронных распадов столь малы, что возникают сомнения в возможности их экспериментального измерения, по крайней мере из данных о длинах пробегов. За время 10-24 с фотон проходит расстояние, меньшее поперечника протона. Тем не менее, существует надежный метод измерения не только малых времен жизни, но и инвариантных масс маложивущих частиц. Этот метод называется методом спектра инвариантных масс.

Идея метода основана на использовании одного важного закона. Он состоит в следующем. Амплитуда вероятности застать частицу в распадающемся состоянии описывается вращающейся с угловой скоростью w0 стрелкой, экспоненциально уменьшающейся длины (уменьшающаяся длина отражает тот факт, что вероятность застать частицу в данном состоянии уменьшается). Допустим, закон убывания длины стрелки описывается выражением
(1)
Поскольку вероятность P еще застать частицу в данном состоянии равна квадрату модуля амплитуды вероятности, постольку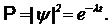
(2)
Как видно, при таком выборе зависимости модуля амплитуды вероятности от времени параметр l равен скорости распада. Один из математических результатов говорит, что описанный выше закон зависимости амплитуды от времени можно представить, как наложение незатухающих вращений стрелок различной длины, каждая из которых вращается со своей частотой. Частоты распределены около значения w0. Квадраты модулей составляющих стрелок зависят от частоты вращения по закону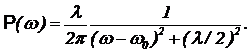
(3)

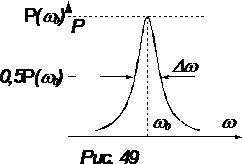График зависимости P(w) имеет форму резонансной кривой (см. рисунок). Максимум кривой P(w) приходится на частоту w=w0. Горизонтальная прямая на высоте P(w0)/2 пересекает график в точках w=w0±l/2, т. е. данная резонансная кривая имеет ширину Dw=l.

Проведем физическое разъяснение данного математического результата. Допустим, на дифракционную решетку падает поток цугов, каждый из которых представляет собой волну частоты w0, модулированную затухающей экспонентой (1). Первый дифракционный максимум придется на частоту w0, а интенсивность рассеянного решеткой света будет распределена по закону (3). Связь между законом распада состояния и спектральным составом амплитуды вероятности перекликается с тем, как затухающие колебания гармонического осциллятора связаны с формой его резонансной кривой.

Изложенный математический результат имеет такую физическую интерпретацию: распадающееся состояние представляет собой суперпозицию состояний с определенными значениями энергии; распределение значений энергии описывается законом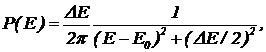
(4)
где E0 — наивероятнейшее значение энергии в смеси, DE — ширина распределения, связанная со скоростью распада состояния l соотношением
DE=ћl. (5)
Это означает, что если проводить измерения энергии системы, находящейся в распадающемся со скоростью l состоянии, то будут наблюдаться случайные значения E. Плотность распределения значений энергии будет описываться законом (4).