Методичка к ргр по электротехнике
1. Общие методы по выполнению и оформлению расчетно-графической работы
Расчетно-графическая работа (РГР) составлена в соответствии с рабочими программами для технологических (неэлектротехнических) специальностей. Она содержит 9 задач по следующим разделам курса: однофазные электрические цепи синусоидального тока; трехфазные цепи; трансформаторы; электрические машины; электропривод; электроника.
РГР состоит из двух частей. В первой части приведены условия и варианты задач. Вторая часть содержит методические указания к решению этих задач. В заданиях на выполнение РГР к каждой задаче дается таблица с числовыми и схемными вариантами.
В РГР №1 входят задачи: 1, 2, 3, 4.
В РГР № 2 входят задачи: 5, 6, 7, 9.
РГР выполняется в отдельной тетради, на обложке которой должны быть указаны название, вариант, группа и ФИО студента. На каждой странице нужно оставлять поля шириной 2-3 см для замечаний преподавателя. Текст, формулы и математические расчеты следует писать четко и аккуратно. Электрические схемы должны вычерчиваться с соблюдением условных графических изображений электротехнических элементов. Графики и векторные диаграммы должны выполняться на миллиметровой бумаге, а затем вклеиваться в тетрадь, либо на листе ученической тетради в клетку.
В конце работы студент ставит свою подпись и дату выполнения. Если по работе имеются замечания, то необходимые исправления делаются в той же тетради после заключения преподавателя.
Работа, выполненная не по своему варианту, в неполном объеме или небрежно оформленная, к проверке не принимается.
2. Условия и варианты задач
Задача 1. Для разветвленной электрической цепи постоянного тока (рис.1) по заданным сопротивлениям и ЭДС определить:
а) токи во всех ветвях методом непосредственного применения законов Кирхгофа;
б) токи во всех ветвях методом контурных токов;
в) проверить баланс мощностей.
Таблица 1
|
Номер варианта |
Данные к задаче 1 |
||||||||
|
Е1,В |
Е2,В |
Е3,В |
R1,Ом |
R2,Ом |
R3,Ом |
R4,Ом |
R5,Ом |
R6,Ом |
|
|
1 |
10 |
12 |
8 |
2 |
2 |
4 |
4 |
6 |
6 |
|
2 |
8 |
10 |
6 |
1 |
1 |
1 |
6 |
6 |
4 |
|
3 |
9 |
14 |
6 |
6 |
6 |
2 |
6 |
1 |
1 |
|
4 |
10 |
10 |
9 |
2 |
2 |
2 |
6 |
6 |
4 |
|
5 |
12 |
18 |
20 |
10 |
6 |
8 |
12 |
10 |
8 |
|
6 |
19 |
14 |
8 |
8 |
8 |
10 |
12 |
14 |
10 |
|
7 |
11 |
12 |
9 |
6 |
6 |
4 |
8 |
6 |
8 |
|
8 |
6 |
12 |
10 |
2 |
2 |
4 |
4 |
2 |
2 |
|
9 |
8 |
10 |
12 |
4 |
6 |
4 |
6 |
10 |
8 |
|
10 |
10 |
11 |
14 |
6 |
8 |
12 |
10 |
8 |
6 |
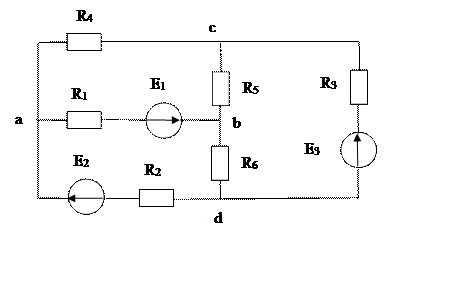
Рис.1. Схема к задаче 1
Задача 2. В цепи рис.2 активные и реактивные сопротивления в параллельных ветвях соответственно равны R1, X1; R2, X2, сопротивления в неразветвленной части цепи R0, X0. Напряжение на зажимах цепи равно U. Определить методом комплексных чисел показания амперметра (электромагнитной системы) и обоих ваттметров. Составить баланс активных и реактивных мощностей. Построить векторную диаграмму.
Таблица 2
|
Номер варианта |
Данные к задаче 2 |
||||||
|
U, В |
R0,Ом |
Х0,Ом |
R1,Ом |
Х1,Ом |
R2,Ом |
Х2,Ом |
|
|
1 |
30 |
1 |
2 |
3 |
4 |
3 |
4 |
|
2 |
40 |
1 |
-2 |
4 |
3 |
4 |
3 |
|
3 |
50 |
2 |
1 |
5 |
0 |
6 |
8 |
|
4 |
35 |
1 |
-1 |
6 |
8 |
8 |
6 |
|
5 |
44 |
1 |
2 |
8 |
6 |
9 |
12 |
|
6 |
50 |
1 |
-2 |
10 |
0 |
12 |
9 |
|
7 |
40 |
2 |
1 |
6 |
8 |
8 |
-6 |
|
8 |
45 |
2 |
1 |
8 |
6 |
6 |
-8 |
|
9 |
30 |
1 |
1 |
4 |
3 |
4 |
-3 |
|
10 |
35 |
1 |
-2 |
5 |
0 |
3 |
-4 |
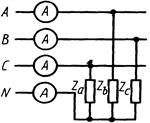
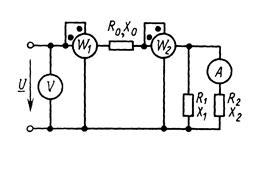
Рис. 2. Схема к задаче 2 Рис. 3. Схема к задаче 3
Задача 3. К трехфазной линии с линейным напряжением UЛ подключена группа однофазных приемников, соединенных по схеме «звезда» с нейтральным проводом (рис. 3). Комплексное сопротивление фаз не симметричного приемника задано. Сопротивление нейтрального провода ![]() пренебрежимо мало. Определить: а) фазные и линейные токи в приемнике, соединенном звездой; б) активную, реактивную и полную мощности на зажимах линии. Построить топографическую диаграмму напряжений и векторную диаграмму токов. Пользуясь векторной диаграммой токов, определить показания каждого из амперметров.
пренебрежимо мало. Определить: а) фазные и линейные токи в приемнике, соединенном звездой; б) активную, реактивную и полную мощности на зажимах линии. Построить топографическую диаграмму напряжений и векторную диаграмму токов. Пользуясь векторной диаграммой токов, определить показания каждого из амперметров.
Таблица 3
|
Номер варианта |
Данные к задаче 3 |
|||
|
U л, В |
Za |
Zb |
Zc |
|
|
1 |
220 |
13+j10 |
8-j6 |
3+j4 |
|
2 |
220 |
10-j13 |
11-j17 |
8-j8 |
|
3 |
380 |
0+j10 |
8-j6 |
11-j19 |
|
4 |
380 |
8,7+j5 |
10+j10 |
4-j3 |
|
5 |
220 |
6+j8 |
8,7-j5 |
0-j5 |
|
6 |
220 |
10+j0 |
20-j11 |
10+j0 |
|
7 |
380 |
19-j11 |
13+j10 |
19-j11 |
|
8 |
380 |
8+j6 |
6-j8 |
15-j10 |
|
9 |
500 |
10+j10 |
18+j0 |
20+j20 |
|
10 |
500 |
8+j8 |
0-j15 |
19-j19 |
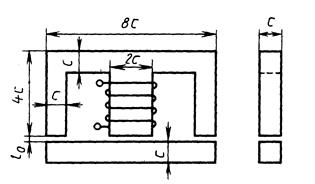
Задача 4. Подъемный электромагнит имеет подковообразный магнитопровод прямоугольного сечения (рис. 4). Материал магнитопровода и якоря – электротехническая сталь. На среднем стержне расположена катушка, состоящая из w витков. Между краями стержней магнитопровода и якорем предусматриваются воздушные зазоры длиной l0 = 0,5 мм. Электромагнит должен развивать подъемную силу Q. Определить требуемое значение тока в катушке.
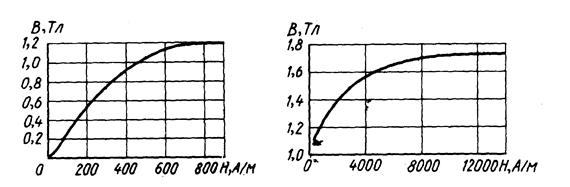
Указания: 1. Подъемная сила электромагнита (на один полюс сердечника) выражается формулой 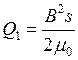 , где s – площадь поперечного сечения воздушного зазора под полюсом. 2. Воспользоваться кривой намагничивания на рис. 5.
, где s – площадь поперечного сечения воздушного зазора под полюсом. 2. Воспользоваться кривой намагничивания на рис. 5.
|
|
Таблица 4
|
Номер варианта |
Данные к задаче 4 |
||
|
с, см |
w |
Q, Н |
|
|
1 |
3 |
200 |
1500 |
|
2 |
3,5 |
200 |
2000 |
|
3 |
4 |
300 |
2500 |
|
4 |
4,5 |
400 |
3000 |
|
5 |
5 |
500 |
4000 |
|
6 |
5,5 |
600 |
5000 |
|
7 |
6 |
700 |
6000 |
|
8 |
6,5 |
800 |
7000 |
|
9 |
7 |
900 |
8000 |
|
10 |
7,5 |
1000 |
9000 |
Задача 5. Трехфазный трансформатор характеризуется следующими данными: номинальная мощность Sн; высшее линейное напряжение U1н; низшее линейное напряжение U2н; мощность потерь холостого хода Рх; изменение напряжения при номинальной нагрузке и cosj2=1 DU %; напряжение короткого замыкания uк; схема соединения обмоток Y/Y. Определить: а) фазные напряжения первичной и вторичной обмоток при холостом ходе; б) коэффициент трансформации; в) номинальные токи в обмотках трансформатора; г) активное и реактивное сопротивления фазы первичной и вторичной обмоток; д) КПД трансформатора при cosj2=0,8 и cosj2=1 и коэффициент загрузки b=0,5; 0,8. Построить векторную диаграмму для одной фазы нагруженного трансформатора при активно-индуктивной нагрузке (cosj2<1).
Указание. Принять, что в опыте короткого замыкания мощность потерь распределяется поровну между обмотками.
Таблица 5
|
Номер варианта |
Данные к задаче 5 |
|||||
|
Sн, кВ×А |
U1н, кВ |
U2н, В |
Рх, Вт |
DU, % |
uк, % |
|
|
1 |
5 |
6 |
400 |
60 |
3,8 |
5 |
|
2 |
5 |
6 |
400 |
100 |
4,0 |
5,5 |
|
3 |
10 |
6 |
400 |
110 |
3,5 |
5 |
|
4 |
10 |
10 |
400 |
140 |
3,45 |
4,5 |
|
5 |
10 |
6 |
400 |
160 |
3,7 |
5,5 |
|
6 |
25 |
6 |
400 |
180 |
3,2 |
5 |
|
7 |
25 |
10 |
400 |
220 |
3,4 |
4,5 |
|
8 |
25 |
10 |
400 |
200 |
3,1 |
5 |
|
9 |
40 |
6 |
400 |
250 |
2,9 |
5,5 |
|
10 |
40 |
10 |
400 |
300 |
2,8 |
4,5 |
Задача 6. Электродвигатель постоянного тока с параллельным возбуждением характеризуется следующими номинальными величинами: напряжение Uн; мощность на валу Рн; частота вращения якоря пн; КПД hн; сопротивление цепи якоря Rя; сопротивление цепи возбуждения Rв. Определить: а) частоту вращения якоря при холостом ходе; б) частоту вращения якоря при номинальном моменте на валу двигателя и включении в цепь якоря добавочного сопротивления, равного 3Rя. Построить естественную и реостатную механические характеристики п(М) электродвигателя.
Указание. Реакцией якоря и током холостого хода якоря пренебречь.
Таблица 6
|
Номер варианта |
Данные к задаче 6 |
|||||
|
Uн, В |
Рн, кВт |
пн, об/мин |
hн, % |
Rя, Ом |
Rв, Ом |
|
|
1 |
110 |
1,0 |
3000 |
77 |
1,2 |
220 |
|
2 |
110 |
1,5 |
3000 |
76 |
0,8 |
160 |
|
3 |
110 |
2,2 |
3000 |
80 |
0,48 |
110 |
|
4 |
110 |
3,2 |
3000 |
78,5 |
0,34 |
80 |
|
5 |
110 |
4,5 |
1500 |
80 |
0,23 |
70 |
|
6 |
220 |
6 |
1500 |
82,5 |
0,62 |
220 |
|
7 |
220 |
8 |
3000 |
83,5 |
0,44 |
110 |
|
8 |
220 |
11 |
1500 |
84 |
0,31 |
185 |
|
9 |
220 |
14 |
1500 |
86,5 |
0,21 |
135 |
|
10 |
220 |
19 |
1500 |
84,5 |
0,16 |
110 |
Задача 7. Трехфазный асинхронный двигатель с короткозамкнутым ротором питается от сети с линейным напряжением 380 В. Величины, характеризующие номинальный режим двигателя: мощность на валу Р2н; частота вращения ротора п2н; коэффициент мощности cosjн; КПД hн. Обмотки фаз статора соединены звездой. Кратность критического момента относительно номинального КМ=Мк/Мн. Определить: а) номинальный ток в фазе обмотки статора; б) число пар полюсов обмотки статора; в) номинальное скольжение; г) номинальный момент на валу ротора; д) критический момент; е) критическое скольжение (пользуясь формулой 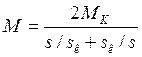 ); ж) значения моментов, соответствующие значениям скольжения: sн; sк; 0,1; 0,2; 0,4; 0,6; 0,8; 1,0 (по формуле п. е); з) пусковой момент при снижении напряжения в сети на 10 %. Построить механическую характеристику п(М) электродвигателя.
); ж) значения моментов, соответствующие значениям скольжения: sн; sк; 0,1; 0,2; 0,4; 0,6; 0,8; 1,0 (по формуле п. е); з) пусковой момент при снижении напряжения в сети на 10 %. Построить механическую характеристику п(М) электродвигателя.
Таблица 7
|
Номер варианта |
Данные к задаче 7 |
||||
|
Р2н, кВт |
п2н, об/мин |
cosj1н |
hн, % |
КМ |
|
|
1 |
1,1 |
2800 |
0,87 |
79,5 |
2,2 |
|
2 |
1,5 |
2825 |
0,88 |
80,5 |
2,2 |
|
3 |
2,2 |
2850 |
0,89 |
83,0 |
2,2 |
|
4 |
3,0 |
1430 |
0,84 |
83,5 |
2,2 |
|
5 |
4,0 |
1430 |
0,85 |
86,0 |
2,2 |
|
6 |
5,5 |
1440 |
0,86 |
88,0 |
2,2 |
|
7 |
7,5 |
1440 |
0,87 |
88,5 |
2,2 |
|
8 |
10 |
960 |
0,89 |
88,0 |
1,8 |
|
9 |
13 |
960 |
0,89 |
88,0 |
1,8 |
|
10 |
17 |
960 |
0,90 |
90,0 |
1,8 |
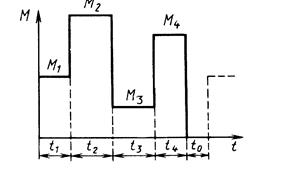
Задача 8. Металлорежущий станок приводиться во вращение АД. Момент на валу двигателя за цикл работы станка изображается нагрузочной диаграммой (рис. 6). Допустимая для двигателя кратность максимального момента КМ=Мmax/Мн. Номинальная частота вращения ротора двигателя пн. Интервал между циклами t0=0,5 мин. Определить: а) необходимую мощность ЭД по условиям нагрева (исходя из среднеквадратичной мощности) и допустимой перегрузки; б) энергию, потребляемую из сети ЭД, за один цикл работы станка.
Указание. Изменением скольжения пренебречь.
|
Таблица 8
|
Номер вари-анта |
Данные к задаче 8 |
|||||||||
|
М1, Н×м |
М2, Н×м |
М3, Н×м |
М4, Н×м |
КМ |
пн, об/мин |
t1, мин |
t2, мин |
t3, мин |
t4, мин |
|
|
1 |
20 |
30 |
10 |
25 |
2,2 |
3000 |
0,5 |
1,0 |
1,5 |
1,3 |
|
2 |
20 |
35 |
10 |
30 |
2,2 |
3000 |
0,6 |
1,1 |
1,6 |
1,4 |
|
3 |
20 |
40 |
15 |
35 |
2,2 |
3000 |
0,7 |
1,2 |
1,7 |
1,5 |
|
4 |
25 |
40 |
15 |
35 |
2,0 |
1500 |
0,8 |
1,3 |
1,8 |
1,6 |
|
5 |
25 |
50 |
15 |
40 |
2,0 |
1500 |
0,9 |
1,4 |
1,9 |
1,6 |
|
6 |
25 |
60 |
20 |
50 |
2,0 |
1000 |
1,0 |
1,5 |
1,5 |
1,7 |
|
7 |
30 |
75 |
20 |
60 |
1,8 |
1000 |
0,9 |
1,2 |
1,6 |
1,8 |
|
8 |
40 |
75 |
25 |
65 |
1,8 |
1000 |
0,8 |
1,0 |
1,7 |
1,9 |
|
9 |
45 |
80 |
30 |
70 |
1,7 |
1000 |
0,7 |
0,8 |
1,8 |
2 |
|
10 |
60 |
80 |
30 |
70 |
1,9 |
1000 |
0,6 |
0,9 |
1,9 |
2 |
Задача 9. Провести графоаналитическое исследование режима работы в классе А и определить основные параметры транзисторного усилительного каскада в схеме с ОЭ при одном источнике питания Ек с автоматическим смещением и эмиттерной стабилизацией рабочего режима, т. е. с последовательной отрицательной обратной связью по постоянной состовляющей эмиттерного тока, проходящего через Rэ (см. рис. 19, 20).
Тип биполярного транзистора для каскада выбрать по своему варианту шифра из табл. 11, а семейство статических выходных вольт-амперных характеристик и одну входную характеристику при Uкэ = -5 В взять по рис. 21-33, некоторые предельно-допустимые параметры транзистора – из табл. 11 или справочника. Рабочая температура транзисторов находится в пределах 20-30 °С.
Определить Кi, Кu, Rp, b, Rвх. каск, Rвых. каск, Rк = Rн, Rб = (R1||R2), Rэ, Ек, Сэ, Сp, Iб0, Iк0, Iэ0, Iдел, Uбе0, Uке0 ± Um вх ± Um вых.
3. Примеры решения задач.
Пример 1. Разветвленная электрическая цепь (рис. 7) имеет следующие параметры: R1=2 Ом; R2=2 Ом; R3=6 Ом; R4=4 Ом; R5=4 Ом; R6=8 Ом; Е1=24 В; Е2=24 В; Е3=12 B. Определить токи ветвей методом применения законов Кирхгофа и методом контурных токов. Проверить баланс мощностей.
|
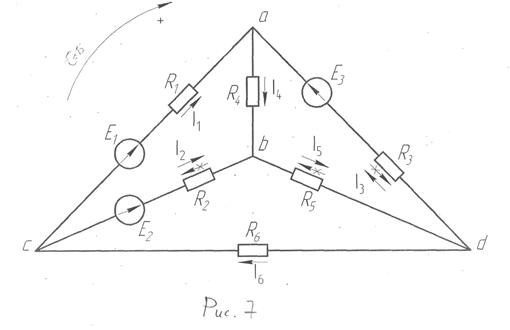
Расчет методом применения законов Кирхгофа
Произвольно наносим положительные направления токов и положительное направление обхода контуров (рис. 1). Составляем (n-1) уравнений по первому закону Кирхгофа, где n – число узлов.
Алгебраическая сумма токов в узле равна нулю. Ток, притекающий к узлу, берем со знаком «+», вытекающий – со знаком «-»
1) узел «а» : I1- I4 – I3 =0;
2) узел «b» : I4 – I2 + I5 =0;
3) узел «с» : — I1 + I2 + I6 =0.
Остальные [m-(n-1)] уравнения составляем по второму закону Кирхгофа, где m – число ветвей (неизвестных токов).
Алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжений берем со знаком «+» если их направление совпадает с положительным направлением обхода контура, в противоположном случае со знаком «-».
4) контур «abca» : I1 R1 + I4 R4 + I2 R2 = E1 – E2 ;
5) контур «adba» : I3 R3 + I5 R5 – I4 R4 = — E3 ;
6) контур «cbdc» : — I2 R2 – I5 R5 + I6 R6 = E2
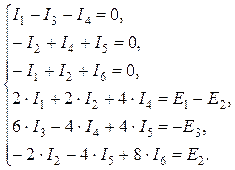
Решение всех систем уравнений производим при помощи ЭВМ. Для решения системы составляем матрицу:
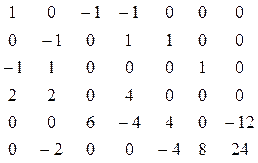
Результаты расчета по программе «Linsi»:
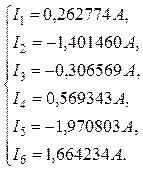
Отрицательный результат означает, что ток течёт в направлении противоположном выбранному.
Расчет цепей методом контурных токов.
Исходит из того, что в любом независимом контуре (ячейки) течёт свой контурный ток.
Произвольно задаёмся направлением контурных токов (рис. 8).
 Рис. 8. Схема для расчёта методом контурных токов
Рис. 8. Схема для расчёта методом контурных токов
Составляем для выбранных контуров уравнения по второму закону Кирхгофа относительно контурных токов:
1) контур «abca»: IK1(R1+R2+R4) – IK2R4 – IK3R2 = E1 – E2;
2) контур «adba» : IK2(R3 + R4 + R5) – IK1R4 – IK3R5 = — E3 ;
3) контур «cbdc» : IK3(R2 + R5 + R6) – IK1R2 – IK2R5 = E2 .
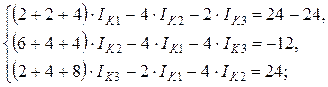
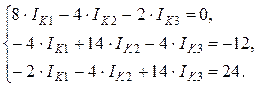
Для решения системы составим матрицу:
![]()
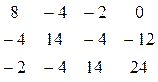
Результат работы программы «Linsi»:
![]()
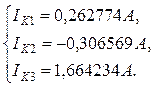
Отрицательный результат означает, что контурный ток течёт в направлении противоположном выбранному.
Находим фактические токи как сумму или разность соответствующих контурных токов (во внешних ветвях они равны контурным, а во внутренних равны разности смежных контурных токов).
I1 =IK1 = 0,26277 A,
I2 =IK3 – IK1 = 1,616236 – 0,066421 = 1,549815 A,
I3 = IK2 = 0,376384 A,
I4 =IK1 + IK2 = 0,066421 + 0,376384 = 0,442805 A,
I5 = IK2 + IK3 = 0,376384 + 1,616236 = 1,99262 A,
I6 =IK3 = 1,616236 A.
Окончательно:
![]()
![]()
![]()
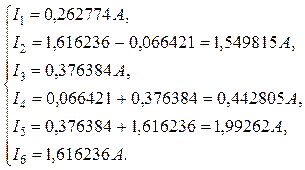
![]()
Проверка баланса мощности.
Мощность, вырабатываемая источниками ЭДС, равна мощности потребляемой приёмниками.
I12×R1+I22×R2+I32×R3+I42×R4+I52×R5+I62×R6=E1×I1+E2×I2+E3×I3;
0,2627742×2+1,4014602×2+0,3065692×6+0,5693432×4+1,9708032×4+1,6642342×8= =43,62045004(Вт)
24×0,262774+24×1,401460+12×0,306569=43,620444(Вт)
43,62045004(Вт) » 43,620444(Вт) – баланс сходится.
Пример 2. Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников, схема которой изображена на рис. 9. Дано: U=120 В, R1=10 Ом, R2=24 Ом, R3=15 Ом, L1=19,1 мГ, С2=455 мкФ; L3=63,5 мГ, f=50 Гц. Определить токи 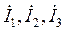 в ветвях цепи, напряжения на участках цепи
в ветвях цепи, напряжения на участках цепи ![]() , активную, реактивную и полную мощности и построить векторную диаграмму на комплексной плоскости.
, активную, реактивную и полную мощности и построить векторную диаграмму на комплексной плоскости.
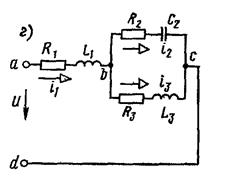
Рис. 9. Схема для примера 2
Решение. Выражаем сопротивления ветвей цепи в комплексной форме:
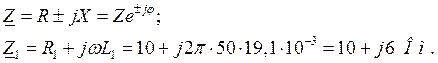
Переходя от алгебраической формы записи комплексного числа к показательной, получаем:
![]()
где 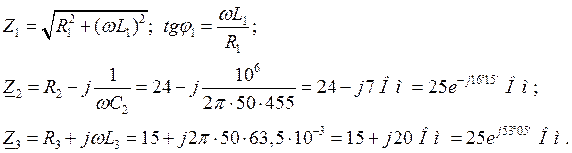
Выражаем заданное напряжение U в комплексной форме. Если начальная фаза напряжения не задана, то ее можно принять равной нулю и располагать вектор напряжения совпадающим с положительным направлением действительной оси. В этом случае мнимая составляющая комплексного числа отсутствует (рис. 10) ![]()
![]()
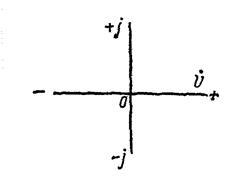
Рис. 10. Вектор напряжения
Полное комплексное сопротивление цепи
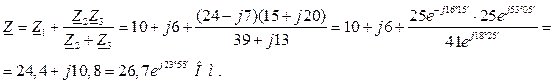
Определяем ток в неразветвленной части цепи
![]()
Токи ![]() и
и ![]() в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:
в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:
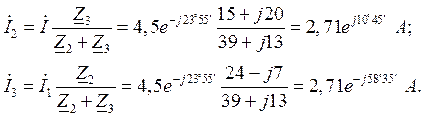
Токи ![]() и
и ![]() можно найти иначе:
можно найти иначе:
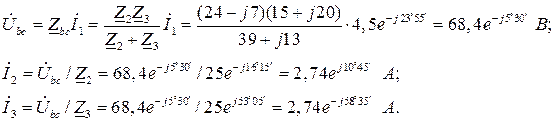
Найдем мощности всей цепи и отдельных ее ветвей:
![]()
Для определения активной и реактивной мощностей полную мощность, выраженную комплексным числом в показательной форме, переводим в алгебраическую форму. Тогда действительная часть комплекса представляет собой активную мощность, а мнимая – реактивную:
![]()
откуда Р=494 Вт; Q=218 вар.
Активную и реактивную мощности можно найти иначе:
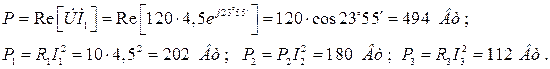
Проверка показывает, что Р=Р1+Р2+Р3.
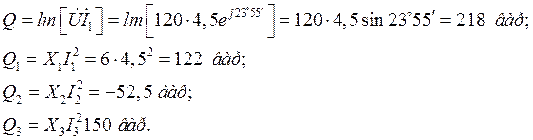
Учитывая, что Q1 и Q3 положительны (реактивная мощность индуктивных катушек), а Q2 отрицательно (реактивная мощность конденсатора), получим Q=Q1-Q2+Q3=218 вар.
На рис. 11 приведена диаграмма токов и напряжений, построенная по расчетным данным. Порядок ее построения следующий: по результатам расчетов отложены векторы токов ![]() и
и ![]() , затем по направлению
, затем по направлению ![]() отложен вектор
отложен вектор ![]() и перпендикулярно к нему в сторону опережения – вектор
и перпендикулярно к нему в сторону опережения – вектор ![]() . Их сумма дает вектор
. Их сумма дает вектор ![]() . Далее в фазе с
. Далее в фазе с ![]() построен вектор
построен вектор ![]() и перпендикулярно к нему в сторону отставания вектор
и перпендикулярно к нему в сторону отставания вектор ![]() , а их сумма дает вектор напряжения на параллельном участке
, а их сумма дает вектор напряжения на параллельном участке ![]() . Тот же вектор можно получить, если в фазе с
. Тот же вектор можно получить, если в фазе с ![]() отложить
отложить ![]() и к нему прибавить вектор
и к нему прибавить вектор 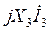 , опережающий
, опережающий ![]() на 90°. Сумма векторов
на 90°. Сумма векторов ![]() и
и ![]() дает вектор приложенного напряжения
дает вектор приложенного напряжения ![]() .
.
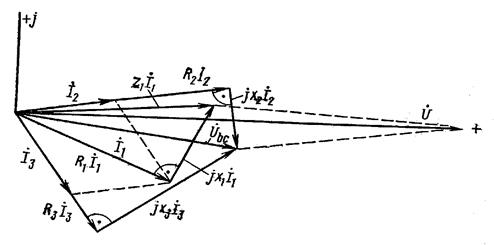
Рис. 11. Векторная диаграмма к примеру 2
Пример 3. В четырехпроводную трехфазную сеть с линейным напряжением ![]() включен звездной приемник, активные и индуктивные сопротивления фаз которого соответственно равны: Ra=3 Ом, Хa=4 Ом, Rb=3 Ом, Xb=5,2 Ом, Rc=4 Ом, Xc=3 Ом (рис. 12). Определить токи в линейных и нейтральном проводах и построить векторную диаграмму.
включен звездной приемник, активные и индуктивные сопротивления фаз которого соответственно равны: Ra=3 Ом, Хa=4 Ом, Rb=3 Ом, Xb=5,2 Ом, Rc=4 Ом, Xc=3 Ом (рис. 12). Определить токи в линейных и нейтральном проводах и построить векторную диаграмму.
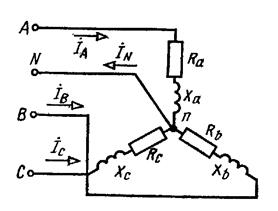
Рис. 12. Схема для примера 3
Решение. Считаем, что вектор фазного напряжения ![]() направлен по действительной оси, тогда
направлен по действительной оси, тогда ![]()
Находим линейные токи:
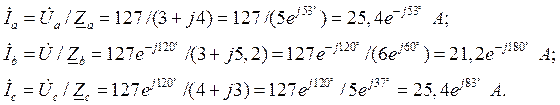
Ток в нейтральном проводе определяется как геометрическая сумма линейных токов:
![]()
Векторная диаграмма показана на рис. 13.
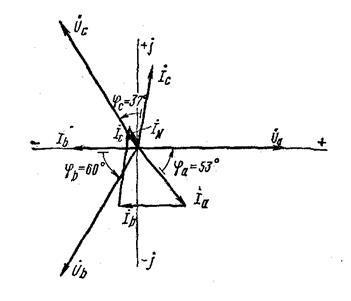
Рис. 13. Векторная диаграмма к примеру 3
При несимметричной нагрузке для определения активной мощности находят мощность каждой фазы отдельно: Рф=UфIфcosj, а мощность всей трехфазной системы получают как сумму мощностей всех фаз или используют схему включения двух ваттметров.
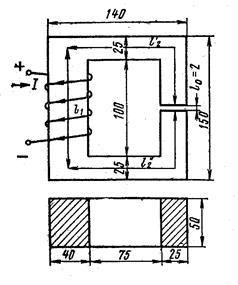 Пример 4. На рис. 14 даны геометрические размеры магнитопровода цепи в миллиметрах, выполненного из электротехнической стали марки 1211. Требуется определить магнитодвижущую силу F=wI, которая необходима для создания магнитного потока Ф=2×10-3 Вб, значение тока в катушке I, содержащей w=1000 вит, и индуктивность катушки L.
Пример 4. На рис. 14 даны геометрические размеры магнитопровода цепи в миллиметрах, выполненного из электротехнической стали марки 1211. Требуется определить магнитодвижущую силу F=wI, которая необходима для создания магнитного потока Ф=2×10-3 Вб, значение тока в катушке I, содержащей w=1000 вит, и индуктивность катушки L.
![]() Решение. Магнитную цепь делим на участки так, чтобы в пределах каждого материал и сечение магнитопровода оставались неизменными. В данном случае таких участков три. Контур, по которому составляем уравнение, пользуясь законом полного тока, проходит по средней магнитной линии:
Решение. Магнитную цепь делим на участки так, чтобы в пределах каждого материал и сечение магнитопровода оставались неизменными. В данном случае таких участков три. Контур, по которому составляем уравнение, пользуясь законом полного тока, проходит по средней магнитной линии:
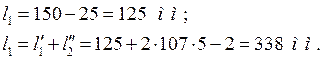
|
Определяем магнитную индукцию в каждом участке цепи, для чего находим сечения магнитопроводов:
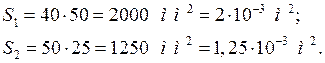
Магнитная индукция
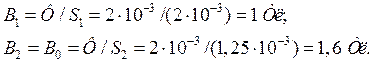
Напряженность магнитного поля для ферромагнитных материалов определяем по кривым намагничивания B=f(H), которые приводятся в справочной и учебной литературе. В данном случае для электротехнической стали марки 1211 имеем: Н1=502 А/м и Н2=4370 А/м. Для воздушного зазора l0 напряженность магнитного поля определяется из равенства
![]()
Искомая магнитодвижущая сила, равная произведению тока на число витков катушки, по которой он протекает, согласно закону полного тока
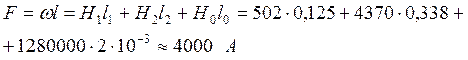
Ток в катушке
![]()
Индуктивность катушки
![]()
где Y — потокосцепление.
Пример 5. Номинальная мощность трехфазного асинхронного двигателя с короткозамкнутым ротором Рном=10 кВт, номинальное напряжение Uном=380 В, номинальная частота вращения ротора nном=1420 об/мин, номинальный к. п.д. hном=0,84 и номинальный коэффициент мощности cosjном=0,85. Кратность пускового тока Iпуск/Iном=6,5, а перегрузочная способность двигателя l=1,8. Определить: 1) потребляемую мощность; 2) номинальный и максимальный (критический) вращающие моменты; 3) пусковой ток; 4) номинальное и критическое скольжения. Построить механические характеристики M=f(S) и W=f(M).
Решение. Потребляемая мощность
![]()
Номинальный и максимальный моменты:
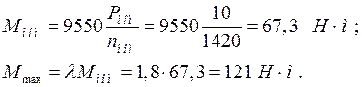
Номинальный и пусковой токи:
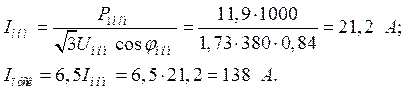
Номинальное и критическое скольжения:
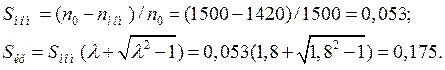
Механическая характеристика M=f(S) строится по уравнению
![]()
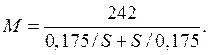
Задаваясь скольжением S от 0 до 1, подсчитываем вращающий момент. Скорость вращения ротора определяем из уравнения 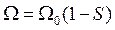 . Расчетные данные приведены в табл. 9. Характеристики, построенные по данным таблицы, изображены на рис. 15, а, б.
. Расчетные данные приведены в табл. 9. Характеристики, построенные по данным таблицы, изображены на рис. 15, а, б.
Таблица 9
|
S |
W, 1/с |
М, Н×м |
S |
W, 1/с |
М, Н×м |
|
0,053 |
149 |
67,3 |
0,5 |
79 |
75,5 |
|
01, |
142 |
104,3 |
0,6 |
63 |
65,2 |
|
0,175 |
130 |
121,0 |
0,7 |
48 |
57,0 |
|
0,2 |
126 |
120,5 |
0,8 |
31,6 |
50,5 |
|
0,3 |
110 |
105,3 |
0,9 |
15,8 |
45,5 |
|
0,4 |
94 |
88,8 |
1,0 |
0 |
41,2 |
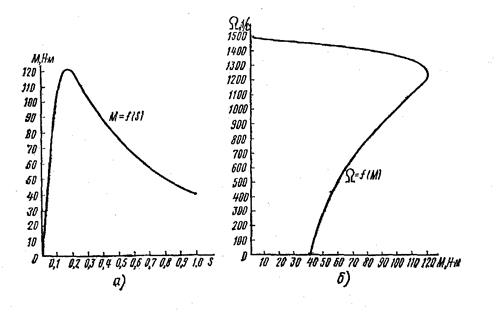
Рис. 15. Механические характеристики
Пример 6. Двигатель параллельного возбуждения, присоединенный к сети с напряжением Uном = 220 В, потребляет при номинальной нагрузке ток Iном=20,5 А, при холостом ходе – I0 = 2,35 А. Сопротивление обмотки якоря Rя = 0,75 Ом, а в цепи возбуждения Rв = 258 Ом. Номинальная частота вращения nном = 1025 об/мин. Определить номинальную мощность двигателя (на валу), номинальный к. п.д., номинальный вращающий момент, пусковой ток при пуске двигателя без пускового реостата, сопротивление пускового реостата для условия Iпуск = 2,5Iном и пусковой момент при пуске двигателя с реостатом. Построить естественную механическую характеристику двигателя. При решении принять, что магнитные и механические потери не зависят от нагрузки.
Решение. Номинальная мощность на валу двигателя
![]()
где ![]() — потери в двигателе; Р1ном – потребляемая мощность;
— потери в двигателе; Р1ном – потребляемая мощность;
![]()
Для определения потерь в цепи якоря и цепи возбуждения надо знать ток в цепи якоря Iя. ном и ток возбуждения Iв:
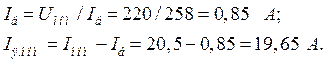
Потери в обмотке якоря и в цепи возбуждения:
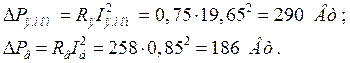
Магнитные и механические потери:
![]()
где ![]()
![]() — потери в обмотке якоря при холостом ходе двигателя:
— потери в обмотке якоря при холостом ходе двигателя:
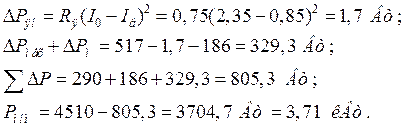
Номинальный к. п.д.
![]()
Номинальный вращающий момент
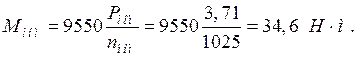
Пусковой ток двигателя при пуске без реостата
![]()
Сопротивление пускового реостата определяется из равенства
![]()
откуда
![]()
Определяем пусковой момент двигателя при пуске с реостатом. Известно, что вращающий момент двигателя определяется уравнением
![]()
Для режима номинальной нагрузки выражение выше принимает вид
![]()
а для пускового режима
![]()
Полагая магнитный поток в двигателе постоянным, возьмем отношение моментов
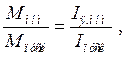
откуда
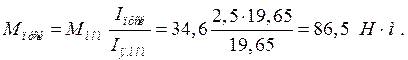
Естественная механическая характеристика W=f(M) (прямая линия) строится по двум точкам: 1) в режиме холостого хода при М=0 частота вращения 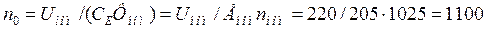 об/мин, где противо-э. д.с.
об/мин, где противо-э. д.с. 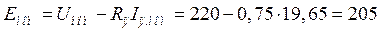 В. Угловая скорость вращения якоря
В. Угловая скорость вращения якоря ![]() 1/с; 2) при номинальной нагрузке М=Мном угловая скорость вращения якоря
1/с; 2) при номинальной нагрузке М=Мном угловая скорость вращения якоря 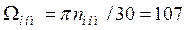 1/с.
1/с.
Пример 7. Для трехфазного трансформатора мощностью Sном=100 кВА, соединение обмоток которого Y/Y0 – 0 известно: номинальное напряжение на зажимах первичной обмотки трансформатора U1ном=6000 В, напряжение холостого хода на зажимах вторичной обмотки трансформатора U20=400 В, напряжение короткого замыкания ик=5,5 %, мощность короткого замыкания Рк=2400 Вт, мощность холостого хода Р0=600 Вт, ток холостого хода I0=0,07I1ном.
Определить: 1) сопротивление обмоток трансформатора R1, X1, R2 и Х2; 2) эквивалентное сопротивление Z0 (сопротивление намагничивающей цепи) и его составляющие R0 и Х0, которыми заменяется магнитная цепь трансформатора; 3) угол магнитных потерь d.
Построить характеристики трансформатора: 1) зависимость U2=f1(b) напряжения U2 от нагрузки (внешняя характеристика); 2) зависимость h=f2(b) коэффициента полезного действия от нагрузки; b — коэффициент нагрузки трансформатора (коэффициент мощности нагрузки принять cosj2=0,75).
Построить векторную диаграмму трансформатора при нагрузке, составляющей 0,8 от номинальной мощности трансформатора Sном и cosj2=0,75.
Решение. Определяем номинальный ток первичной обмотки:
![]()
Определяем ток холостого хода и cosj0:
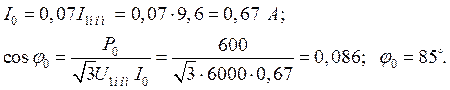
Находим угол магнитных потерь: 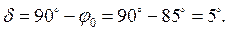
Определяем сопротивления обмоток.
Сопротивления
короткого замыкания:
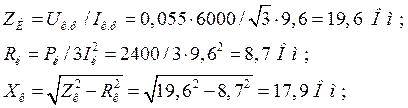
первичной обмотки:
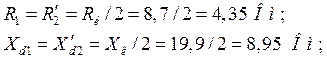
вторичной обмотки:
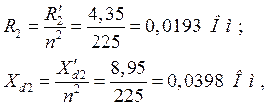
где ![]()
Определяем сопротивления намагничивающей цепи:
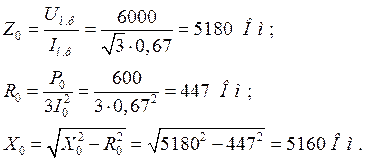
Для построения внешней характеристики U2=f1(b) находим потерю напряжения во вторичной обмотке трансформатора
![]() (1)
(1)
где иа%, ир% — соответственно активное и реактивное падения напряжений; 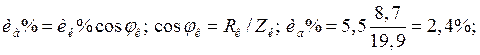
![]()
Напряжение на зажимах вторичной обмотки трансформатора определяем по формуле
![]() (2)
(2)
Задаваясь различными значениями b, по формулам (1) и (2) определяем напряжение U2 (см. табл. 4).
Для построения зависимости h=f2(b) расчет к. п.д. производим по формуле
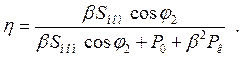
Результаты расчета сведены в табл. 10. Полученные характеристики показаны на рис. 16.
Таблица 10
|
b |
DU2, % |
U2, B |
h |
b |
DU2, % |
U2, B |
h |
|
0,01 |
— |
— |
0,555 |
0,4 |
2,028 |
391,89 |
0,967 |
|
0,025 |
— |
— |
0,757 |
0,5 |
2,535 |
389,86 |
0,969 |
|
0,05 |
— |
— |
0,904 |
0,6 |
3,042 |
287,83 |
0,967 |
|
0,1 |
0,507 |
397,97 |
0,924 |
0,7 |
3,549 |
385,80 |
0,966 |
|
0,2 |
1,014 |
395,94 |
0,956 |
0,8 |
4,056 |
383,78 |
0,964 |
|
0,3 |
1,521 |
393,92 |
0,965 |
0,9 |
4,563 |
381,75 |
0,963 |
|
1,0 |
5,070 |
379,72 |
0,962 |
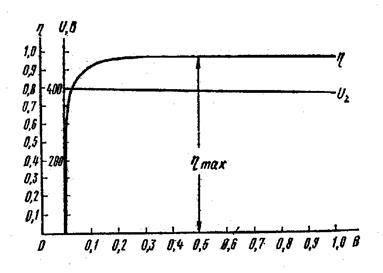
Рис. 16. Характеристики трансформатора
Определяем, при какой нагрузке трансформатор имеет максимальный к. п.д.:
![]()
Построение векторной диаграммы начнем с вектора фазного напряжения ![]() , значение которого для b=0,80 и cosj2=0,75 равно
, значение которого для b=0,80 и cosj2=0,75 равно
![]()
Приведенное значение вторичного напряжения
![]()
Вектор тока ![]() отстает по фазе от вектора
отстает по фазе от вектора ![]() на заданный угол j2 и равен
на заданный угол j2 и равен
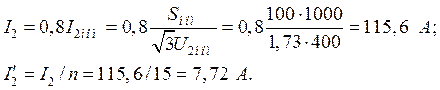
Падения напряжения во вторичной обмотке: 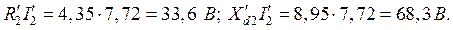
Электродвижущую силу ![]() находим из уравнения электрического состояния, составленного по второму закону Кирхгофа, для вторичной цепи:
находим из уравнения электрического состояния, составленного по второму закону Кирхгофа, для вторичной цепи: ![]()
Вектор магнитного потока Фm опережает вектор ![]() на 90°; а ток холостого хода I0 опережает магнитный поток Фm на угол потерь d. Ток в первичной обмотке трансформатора I1 получаем из уравнения магнитодвижущих сил
на 90°; а ток холостого хода I0 опережает магнитный поток Фm на угол потерь d. Ток в первичной обмотке трансформатора I1 получаем из уравнения магнитодвижущих сил
![]()
где ![]() .
.
Вектор напряжения первичной обмотки трансформатора ![]() определяем из уравнения электрического состояния, составленного по второму закону Кирхгофа для первичной цепи:
определяем из уравнения электрического состояния, составленного по второму закону Кирхгофа для первичной цепи:
![]()
Током холостого хода I0 можно пренебречь (так как он мал) и принять 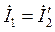 или определить I1 по диаграмме. Тогда падения напряжений в первичной обмотке будут:
или определить I1 по диаграмме. Тогда падения напряжений в первичной обмотке будут: ![]() .
.
Векторная диаграмма трансформатора приведена на рис. 14.
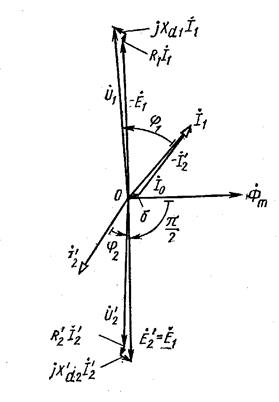
Рис. 17. Векторная диаграмма трансформатора
Пример 8. Определить необходимую мощность двигателя для привода механизма, режим работы которого задан нагрузочной диаграммой на рис. 6. По технологическим условиям следует использовать асинхронный двигатель с короткозамкнутым ротором. Двигатель должен иметь частоту вращения n = 980 об/мин, помещение, где установлен двигатель, — сухое, без пыли и грязи.
Решение. В данном случае режим работы представляет собой длительную переменную нагрузку. Мощность двигателя подбирают при подобных режимах работы по эквивалентной мощности, которая равна
Pэк = 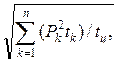
где tц – время цикла работы,
tп = t1 + t2 + t3 =20 + 30 + 15 = 65 с;
Pэк = 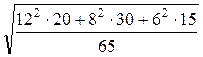 =9,05 кВт.
=9,05 кВт.
По данным каталога в качестве приводимого двигателя можно использовать асинхронный короткозамкнутый двигатель в защищенном исполнении типа А2-61-6; 380/220 B; Pном=10 кВт, nном=965 об/мин; hном=0,870; Мпуск/Мном=1,2; Mmax/Mном=1,8.
В ряде случаев момент нагрузки на отдельных участках оказывается больше максимально допустимого момента двигателя, и асинхронный двигатель может остановиться. Поэтому после выбора двигателя его необходимо проверить по перегрузочной способности исходя из условия Мmax£Mmax доп, где Мmax – максимальный момент на валу двигателя; Mmax доп – максимально допустимый момент двигателя. Для асинхронного двигателя Мmax доп = 0,9 Мкр. Здесь Мкр – критический (максимальный) момент двигателя.
В данном примере:
номинальный момент двигателя
Мном = 9550Pном/nном = 9550×10/965 = 99 H×м,
максимальный (критический) момент
Мкр=lМном=1,8×99= 178 Н×м,
максимальный статический момент
Мст=9550Р1/n =9550 × 12/980 = 117 Н × м.
Перегрузочной способности двигатель удовлетворяет, так как выполняется условие 0,9Мкр = 0,9× 178 +160>Мст = 117.
В том случае, когда нагрузочные двиаграммы заданы моментом М= f (t) или током I= f (t), мощность двигателей выбирают либо по эквивалентному моменту
Мэк = 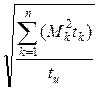 ,
,
либо по эквивалентному току
Iэк =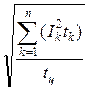 .
.
Пример 9. Рекомендуется такая последовательность решения задачи №9.
1. Записать необходимые параметры заданного транзистора, изобразить схему усилительного каскада (см. рис. 19), объяснить назначение каждого элемента схемы, выбрать значение напряжения источника питания Ек<Uкэ max доп, чтобы Ек»(1,2¸1,5)2Um вых.
2. Перечертить на миллиметровую бумагу входную характеристику Iб=f(Uбэ) при Uкэ=-5 В и семейство выходных вольт-амперных характеристик Iк=f(Uкэ) при Iб=const, на которых по нескольким точкам построить кривую допустимой мощности, рассеиваемой транзистором, Рк=IкUк=const (см. табл. 11) при нормальной рабочей температуре. Ниже этой кривой из точки Uкэ=Ек, выбрав наиболее подходящий угол наклона, провести нагрузочную линию Uкэ=Ек-Iк(Rк+Rэ), на которой выбрать и отметить положение рабочей точки покоя в режиме класса А и допустимые при этом пределы изменения амплитуды базового тока ±Im б, соответствующие максимальному значению входного сигнала. Положение рабочей точки на входной динамической (переходной) характеристике должно соответствовать значению тока Iб0, при котором выбрана рабочая точка на пересечении линией нагрузки и выходной характеристики.
На графиках выходных и входной характеристик изобразить (подобно рис. 4) кривые ![]()
3. По графику определить и записать в тетрадь значения:
Iб0; ±Imб=±0,5(Iбmax-Iбmin); Iк0; ±Imк=±0,5(Iкmax-Iкmin); Iэ0=Iб0+Iк0; Uбэ0;
±Umбэ=±Umвх; Uкэ0; ±Umкэ=±Uвых=±0,5(Uкэmax-Uкэmin).
4. Рассчитать:
b=a/(1-a); Rэ=(0,2¸0,3)Ек/Iэ0; rвх. транз=rб+(1+b)rэ»h11э.
5. Задавшись значением сопротивления резистора R1»(2¸5)rвх. транз, определить:
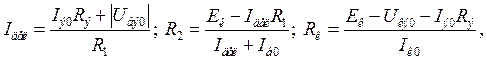
или принять Iдел»(2¸5)Iб0 и найти 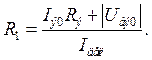
Эквивалентное сопротивление базовой цепи для переменной составляющей входного тока Rб=R1||R2=R1R2/(R1+R2).
Емкость конденсатора при частотной полосе входного сигнала в пределах fн=100 Гц; fв=10000 Гц:
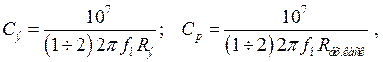
где Сэ, Ср – в мкФ.
Входное и выходное сопротивления каскада:
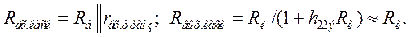
Коэффициенты усиления каскада без дополнительной внешней нагрузки, а также без учета э. д.с. и внутреннего сопротивления входного сигнала
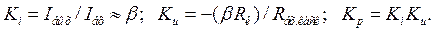
Полезная выходная мощность каскада 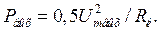
Полная мощность, расходуемая источником питания,
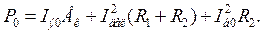
Электрический к. п.д. каскада 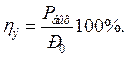
Коэффициент нестабильности каскада по коллекторному току (желательно, чтобы он был меньше)
![]() или
или 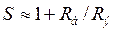 , или точнее
, или точнее 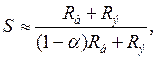
где 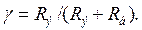
Таблица 11
|
№ вари-анта |
Тип транзистора |
hб-параметры |
Схе-ма |
Предельные значения |
|||||
|
h11б, Ом |
h12б´ ´10-3 |
h21б |
h22б´ ´10-6, см |
Uкэ, В |
Iк, мА |
Рдоп, мВт |
|||
|
1 |
МП42А |
30 |
2 |
-0,96 |
1 |
ОЭ |
15 |
20 |
200 |
|
2 |
МП39 |
30 |
1 |
-0,93 |
1 |
ОЭ |
15 |
20 |
150 |
|
3 |
МП41 |
35 |
1 |
-0,97 |
1 |
ОЭ |
15 |
20 |
150 |
|
4 |
МП113 |
50 |
1 |
-0,96 |
1 |
ОЭ |
10 |
20 |
150 |
|
5 |
МП111 |
50 |
0,5 |
-0,93 |
1 |
ОЭ |
20 |
20 |
150 |
|
6 |
МП39Б |
32 |
1 |
-0,96 |
1 |
ОЭ |
15 |
20 |
150 |
|
7 |
МП36А |
20 |
5 |
-0,96 |
2 |
ОЭ |
15 |
20 |
150 |
|
8 |
П401 |
20 |
2 |
-0,98 |
2 |
ОЭ |
10 |
10 |
50 |
|
9 |
МП41А |
25 |
2 |
-0,98 |
1 |
ОЭ |
15 |
20 |
150 |
|
0 |
МП25 |
25 |
3 |
-0,93 |
2 |
ОЭ |
15 |
20 |
150 |
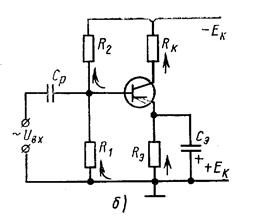
Рис. 19. Схема транзисторного усилительного каскада с эмиттерной стабилизацией рабочего режима
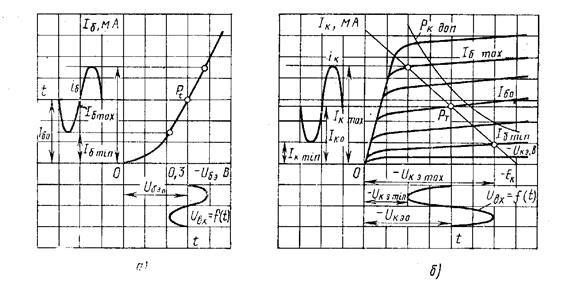
Рис. 20. К определению рабочего режима транзисторного усилительного каскада при работе в классе А по динамической входной (переходной) характеристике (а) и семейству статических выходных характеристик (б)
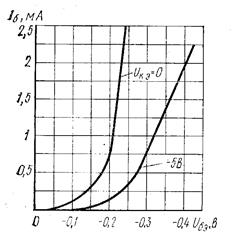
Рис. 21. Усредненные входные характеристики биполярных транзисторов МП39, МП39Б, МП41, МП41А, МП42А в схеме с ОЭ
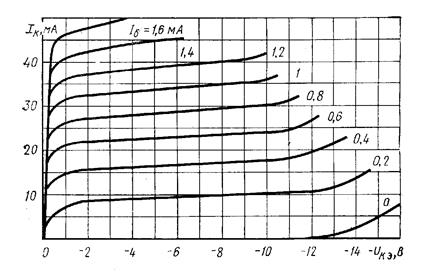
Рис. 22. Усредненные выходные характеристики биполярных транзисторов МП39Б, МП41 в схеме с ОЭ
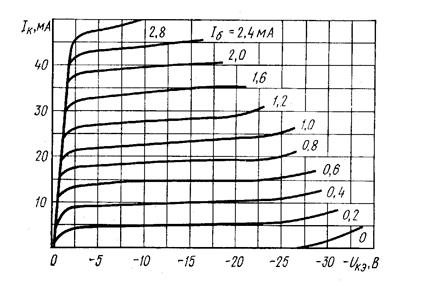
Рис. 23. Усредненные выходные характеристики транзистора МП42А в схеме с ОЭ
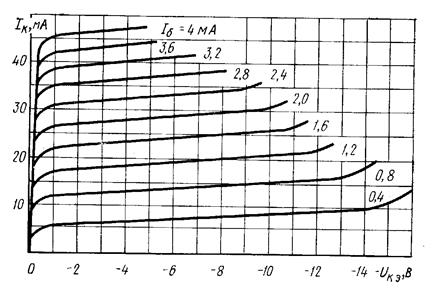
Рис. 24. Усредненные выходные характеристики биполярного транзистора МП39 в схеме с ОЭ
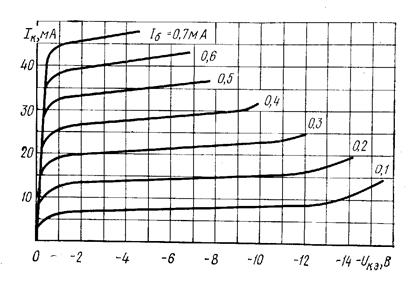
Рис. 25. Усредненные выходные характеристики транзистора МП41А в схеме с ОЭ
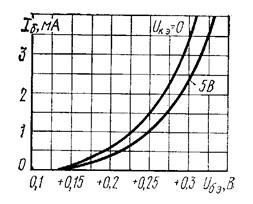
Рис. 26. Усредненные входные характеристики биполярных транзисторов МП25 и МП36А в схеме с ОЭ
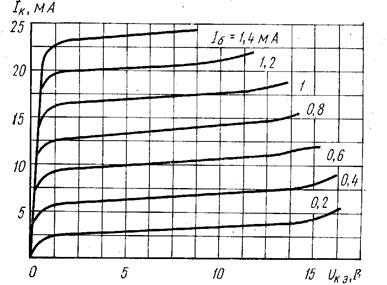
Рис. 27. Усредненные выходные характеристики биполярного транзистора МП25 в схеме с ОЭ
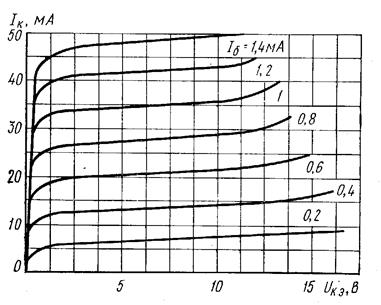
Рис. 28. Усредненные выходные характеристики биполярного транзистора МП36А в схеме с ОЭ
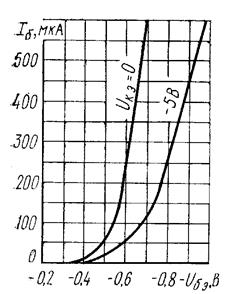
Рис. 29. Усредненные входные характеристики биполярных транзисторов МП111 и МП113 в схеме с ОЭ
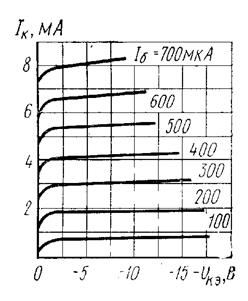
Рис. 30. Усредненные выходные характеристики транзистора МП111 в схеме с ОЭ
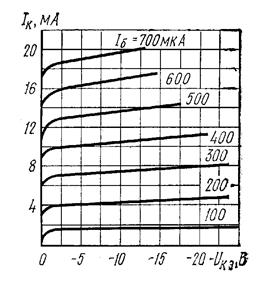
Рис. 31. Усредненные выходные характеристики транзистора МП113 в схеме с ОЭ
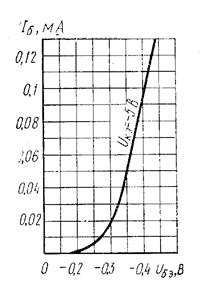
Рис. 32. Усредненные входные характеристики транзистора П401 в схеме с ОЭ
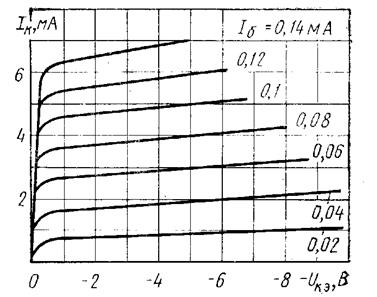
Рис. 33. Выходные характеристики транзистора П401 в схеме с ОЭ


