методичка по электромагнетизму

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО ФИЗИКЕ

Раздел

«ЭЛЕКТРОМАГНЕТИЗМ»

(ОПИСАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ)

ДЛЯ СТУДЕНТОВ ВСЕХ СПЕЦИАЛЬНОСТЕЙ

ВВЕДЕНИЕ

Предлагаемое методическое пособие включает лабораторные работы, в которых изучаются свойства (в основном по отдельности) электрических (работы Э.1 и Э.2) и магнитных полей (работы Э.3, Э.5 Э.7) 1. Такое (обеспечиваемое стационарностью условий) раздельное рассмотрение позволяет сосредоточиться на специфических особенностях каждого из этих полей 2.

В частности, разнообразие геометрической структуры электростатических (и не только!) полей, обусловленное разнообразием возможностей распределения их источников (точечный заряд, диполь, заряженная плоскость и т. д.) изучается в Э.1. Электрические характеристики диэлектрических сред, их измерение с помощью полей, обусловленных устройствами из проводников (конденсаторов), — это вопросы, разбираемые в Э.2.

Большинство лабораторных экспериментов связано с магнитными полями. Это и измерение геомагнитного поля (Э.3), и основанное на измерениях сопоставление полей, создаваемых соленоидом и короткой катушкой (Э.5), и взаимодействие таких полей в рамках механизма взаимной индукции (Э.6), и, наконец, ознакомление с нелинейными полями и явлением гистерезиса ферромагнетиков (Э.7).

Отдельно следует сказать о лабораторной работе Э.4, в которой определяется удельный заряд электрона. Движение электрона происходит в устройстве, называемом магнетроном, под одновременным воздействием электрического и (ортогонального ему) магнитного полей. Измерения в этой работе требуют особой аккуратности для получения правдоподобной зависимости анодного тока от тока в соленоиде, от которой зависят результаты эксперимента.

_____________________

1Лабораторные работы, посвященные изучению электромагнитных полей и волн, составляют содержание самостоятельного методического пособия.

2 Заметим, что по-своему эти поля разделила и природа: так, электрическое поле описывается полярными (истинными) векторами Е и D, а магнитное поле — аксиальными (псевдо-) векторами Н и В.

Лабораторная работа Э.1

МОДЕЛИРОВАНИЕ

СТАЦИОНАРНЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ

Цель работы

Построение эквипотенциальных и силовых линий для различных электрических полей (однородного поля, поля диполя и др.).

Теоретическое введение

Электрическое поле считается полностью охарактеризованным, если в каждой точке пространства известен вектор электрической напряженности . Напряженность в точке с радиус-вектором — это «сила», которая действует на единичный положительный заряд, находящийся в этой точке. Силовой ли­нией электрического поля называется линия, касательная к которой в каждой ее точке совпадает по направлению с вектором . Силовые линии применяют для графического изображения электрических полей. Если в каждой точке напряженность остает­ся неизменной во времени, то электрическое поле называется стацио­нарным. Стационарное электрическое поле потенциально. Это означает, что работа по перемещению любого заряда в таком по­ле не зависит от траектории, по которой осуществляется это пере­мещение, а определяется только положениями начальной и конечной точек траектории. Поэтому стационарное электрическое поле можно описывать не только с помощью вектора напряженности, но и посредством скалярной величины — потенциала . Потенциал в точке с радиус-вектором численно равен работе, которую требуется совершить, чтобы переместить единичный положительный заряд из бесконеч­ности в эту точку. (При этом предполагается, что поле создается ограниченной в пространстве системой зарядов и потенциал на бесконечности равен нулю). По сути дела, потенциал — это потенциальная энергия, которой обладал бы единичный положительный за­ряд, если бы он оказался в точке . Зная потенциал во всех точках поля, легко найти и напряженность поля. Она равна градиенту потенциала, взятому с об­ратным знаком:

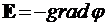. (1)

Градиент скалярной функции в данной точке пространства есть вектор, декартовы компоненты которого суть частные производные этой функции (со знаком «») по соответствующим декартовым координатам, вычисленные в выбранной точке. То есть

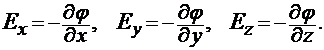(2)

Эквипотенциальной поверхностью в электрическом поле называется поверхность, все точки которой имеют одинаковое значение потенциала. Силовые линии электрического поля могут пересекать эквипотенциальные поверхности только под прямым углом. Рассмотрим скалярное произведение 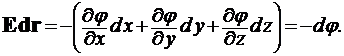Если вектор лежит в плоскости, касательной к эквипотенциальной поверхности, то приращение потенциала равно нулю. Следовательно, электрическое поле перпендикулярно к эквипотенциальной поверхности. Простая формула

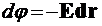(3)

важна для расчета разности потенциалов.

Примеры некоторых конфигураций

электрических полей

а) Однородное поле

Если в некоторой области пространства вектор напряженности электрического поля остается постоянным, т. е. имеет неизменное направление и абсолютную величину, то говорят, что в этой области пространства электрическое поле однородно. В однородном поле связь между напряженностью поля и потенциалом упрощается, приобретая, как следует из (3), вид

Рис. 1 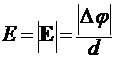, (4)

где — разность потенциалов между любыми двумя эквипотенци-альными плоскостями, а — расстояние между ними.

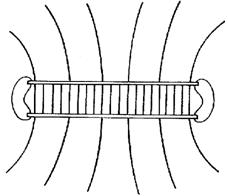
Примером однородного электрического поля служит поле внутри плоского конденсатора (т. е. между двумя близко расположенными параллельными проводящими пластинами, несу­щими равные по модулю, разноименные заряды). Сказанное иллюстрирует рис. 1.

б) Поле диполя

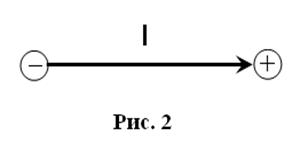Точечный электрический диполь — это система 2-х одинаковых по величине, но разных по знаку, точечных зарядов, расстояние l между которыми значительно меньше расстояния от зарядов до точки наблюдения, где определяется поле системы. Вектор проводится от отрицательного к положительному заряду (см. рис. 2). Так же ориентирован и электрический дипольный момент, который, по определению, равен 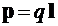. Чтобы составить представ-ление о конфигурации поля диполя, учтем, что картина силовых линий обладает осевой симметрией. Это позволяет ограничиться изображением поля в любой плоскости, содержащей вектор . Соответствующее изображение дано на рис. 3, содержащем силовые (сплошные) и эквипотенциальные (пунктир) линии.