ИЗМЕРЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

Рис. 3

Описание экспериментальной установки

Известно, что в электростатическом случае (когда поле постоянно, а токи отсутствуют) все точки проводника обладают одинаковым потенциалом. Так что внутри проводника электростатического поля нет, и анализ структуры поля связан с наружным пространством.

Особенностью предлагаемой лабораторной работы является то, что присущая электростатическим условиям структура полей изучается в ней в заведомо не электростатических, хотя и стационарных (поле постоянно, но есть постоянный ток) условиях. Причина возможности подобной подмены заключается в следующем. В физике вообще и в электродинамике, в частности, нередко случается, что уравнения для различных физических условий имеют в точности одинаковый вид. Используемые символы (буквы) в них могут, конечно, отличаться, но математическая форма уравнений совпадает. А у одинаковых уравнений — одинаковые решения! Именно это обстоятельство используется авторами этой лабораторной работы. Оказывается, что уравнения и граничные (между областями с разной проводимостью ) соотношения к ним, описывающие электрическое поле в условиях постоянного тока, обнаруживают формальную аналогию с уравнениями электростатического поля в диэлектриках, отличаясь от них лишь заменой диэлектрической проницаемости на . Это позволяет, изучая конфигурацию токов, фактически выявлять конфигурацию электростатического поля.

В данной лабораторной работе металлические электроды, о которых говорилось в начале раздела, разделены не диэлектрической, а проводящей средой. Роль последней играет электропроводящая пленка, к которой прижаты электроды. По пленке течет ток, причем распределение потенциала (а значит, и электрического поля) в ней совпадает с распределением электростатического потенциала (в отсутствие пленки), создаваемого электрически заряженными телами такой же конфигурации, что и электроды.

Схема лабораторной установки дана на рис. 4. На ней указаны основные элементы (обеспечивающие требуемый токовый режим и возможность измерения потенциала): источник постоянного тока, электроды, вольтметр, щуп, указана также ориентация декартовых осей.

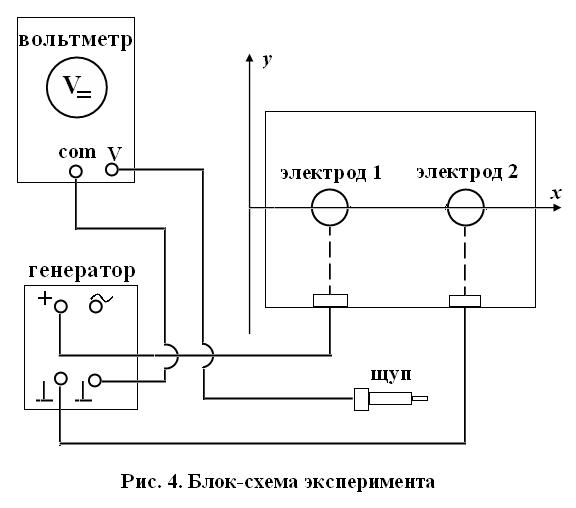
Представленный на схеме (рис. 4) прямоугольник с электродами символизирует место, где располагают плату для моделирования полей. Всего таких плат четыре: 1) плоские электроды; 2) «сектор»; 3) диполь; 4) проводник переменного сечения. На рис. 5 эта область занимает нижнюю половину. Там же представлен так называемый пантограф (устройство для вычерчивания копий). Пантограф содержит горизонтальную рейку, которую можно перемещать в перпендикулярном направлении (по оси у) с отсчетом координаты у по «вертикальной» линейке и фиксировать. По рейке, в свою очередь, перемещают каретку с отсчетом координаты х по горизонтальной линейке. Каретка несет держатель щупа (внизу рис. 5) и упругий кронштейн с держателем фломастера (средняя часть рис. 5). При нажатии щуп касается металлическим электродом проводящей пленки, размещенной на плате. Подключенный к щупу вольтметр регистрирует потенциал соответствующей точки. Когда нужный потенциал найден, нажимают на упругий кронштейн, и фломастер отмечает положение этой точки на миллиметровке. Одновременно регистрируют декартовы координаты этой точки.

Порядок выполнения работы

1.  В пазы каркаса вставьте плоские электроды (плата 1 для моделирования полей). Слегка прижмите плату винтом, выступающим вправо из борта каркаса.

2.  Расположите лист миллиметровой бумаги на пластине конденсатора, наколов углы миллиметровки на шпильки.

3.  Вставьте щуп и фломастер в их держатели.

4.  Подвижную рейку, несущую щуп и фломастер, зафиксируйте винтом, при этом фиксируется и предварительно выбранное значение координаты y.

5.  Перемещая по рейке мелкими шагами каретку, предварительно установленную в крайне левое положение, т. е. изменяя только координату x, измеряйте на каждом шаге по показаниям вольтметра значения потенциала с тем, чтобы найти координаты, соответствующие заранее выбранному его значению. Найденное положение нажатием (с небольшим усилием) на фломастер отмечайте на миллиметровке.

6.  Передвигая подвижную рейку с шагом, равным 10 мм, по оси y вплоть до конца платы, повторите п. 5 для каждого шага.

7.  Повторите пп. 1—6 для оставшихся трех других плат.

Представление результатов эксперимента

На миллиметровках с нанесенной системой точек построить эквипотенциальные линии (с указанием значений соответствующих потенциалов) и силовые линии электрического поля.

Контрольные вопросы

1.  Цель работы.

2.  Каким образом обнаруживается присутствие электрических полей?

3.  Представление о точечном заряде. Сила его взаимодействия с электрическим полем.

4.  Конфигурации полей и их наглядное представление. Силовые линии.

5.  Потенциальность стационарных электрических полей.

6.  Потенциал и его взаимосвязь с полем. Неоднозначность потенциала.

7.  Представление об эквипотенциальных поверхностях и линиях. Взаимная ориентация силовых линий и эквипотенциальных поверхностей (линий).

8.  Однородное поле. Его взаимосвязь с потенциалом.

9.  Напряженность и потенциал поля точечного заряда. Закон Кулона. Потенциальная энергия взаимодействия двух точечных зарядов.

10. Определение электрического дипольного момента.

11. Характеристика метода исследования конфигурации поля, используемого в работе.

12. Содержание лабораторных упражнений. Порядок их выполнения.

Литература

1.  А. В. Астахов, Ю. М. Широков. Курс физики. Т. 2. Электромагнитное поле. М.: «Наука», 1980. 359 с.

2.  И. Е. Иродов. Электромагнетизм. Основные законы. М.-СПб.: Физматлит, 2000. 350 с.

3.  С. М. Крейнин. Физические системы: модели, состояния, уравнения и законы движения. Т. 1. М.: Изд-во ООО «ИПЦ “Маска”», 2009. 476 с.

4.  Д. В. Сивухин. Общий курс физики. Т. 3. Электричество. М.: «Наука», 1977. 688 с.

5.  Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1966. Вып. 5. 296 с.

Лабораторная работа Э.2

ИЗМЕРЕНИЕ

ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

Экспериментальные измерения физических характеристик не всегда являются прямыми, т. е. непосредственно считываемыми с показаний приборов. Чаще производится непосредственное измерение иных величин, которые, однако, связаны с искомыми надежно установленными закономерностями. Так что на последнем этапе ис-следуемая характеристика определяется в результате вычисления по формулам, выражающим указанные закономерности. Процедуру подобного опосредственного определения представляющих интерес физических величин, основанного на экспериментальном исследовании, именуют косвенным измерением. Данная работа имеет дело именно с такого рода измерениями.

Цели работы

1) Теоретический расчет и измерение (двумя способами) электроемкости воздушного конденсатора.

2) Измерение диэлектрических проницаемостей образцов веществ, поочередно располагаемых между пластинами конденсатора.

Теоретическое введение

Диэлектрики (изоляторы) — это вещества, не проводящие электрического тока: их заряды, входящие в состав молекул или ионов, не способны далеко перемещаться. Будучи внесенным во внешнее электрическое поле диэлектрик поляризуется. Явление поляризации независимо от ее механизма (различного у полярных и неполярных молекул и диэлектрических кристаллов) заключается в смещении всех положительных зарядов по направлению поля, а отрицательных зарядов — в прямо противоположном направлении.

Количественное описание явления поляризации опирается на представление о дипольной системе зарядов. Электрический диполь — это система из двух разноименных точечных зарядов, одинаковых по модулю и разделенных расстоянием (плечом диполя) l. Электрическим дипольным моментом этой системы называют вектор 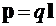, направленный от отрицательного заряда к положительному.

Поляризованный диэлектрик характеризуют вектором P, именуемым поляризованностью (или просто поляризацией), который равен дипольному моменту единицы объема. Если поляризующее поле не слишком велико, то поляризованность Р пропорциональна внешнему полю Е, т. е. P=e0cE . Здесь e0 — электрическая постоянная. Безразмерный коэффициент называется диэлектрической восприимчивостью.