Определение емкости воздушного конденсатора
Основной физической характеристикой диэлектрика служит e — диэлектрическая проницаемость вещества, равная 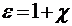 . Для всех веществ
. Для всех веществ ![]() , для вакуума
, для вакуума ![]() . Диэлектрическая проницаемость показывает, во сколько раз поле (или сила кулоновского взаимодействия между зарядами) в диэлектрической среде слабее, чем в вакууме.
. Диэлектрическая проницаемость показывает, во сколько раз поле (или сила кулоновского взаимодействия между зарядами) в диэлектрической среде слабее, чем в вакууме.
Диэлектрическую проницаемость веществ удобно измерять, используя конденсатор. Последний представляет собой систему двух близко расположенных проводников (так называемых обкладок). Поле, создаваемое таким устройством в заряженном состоянии, практически полностью сосредоточено в пространстве между обкладками. Это значит, что силовые линии вектора Е, начинающиеся на одной обкладке, заканчиваются на другой, т. е. заряды на обкладках должны быть одинаковыми по модулю и противоположными по знаку. Основной характеристикой конденсатора является емкость. Последняя определяется формулой
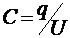 , (1)
, (1)
где U — разность потенциалов между обкладками (называемая также напряжением). B CИ за единицу электроемкости принят фарад (Ф). Емкостью в 1 Ф обладает конденсатор, у которого заряд в 1 Кл создает между обкладками напряжение в 1 В. Фарад — чрезвычайно большая единица емкости. Он соответствует емкости уединенного проводящего шара радиусом в 9 млн км, что в 1400 раз превышает радиус Земли. Поэтому емкости используемых на практике конденсаторов измеряются в микрофарадах и пикофарадах (1мкФ=10-6 Ф, 1пФ=10-12 Ф).
Конденсаторы могут иметь различную геометрическую форму. Существуют, например, сферические, цилиндрические и плоские конденсаторы. В данной лабораторной работе экспериментальные измерения связаны с использованием плоского конденсатора (будем называть его измерительным). Плоский конденсатор — устройство, состоящее из двух параллельных плоских проводящих пластин, расстояние между которыми мало по сравнению с линейными размерами пластин. Если объем между пластинами ничем, кроме воздуха, не заполнен, то устройство называется воздушным конденсатором. Его емкость равна
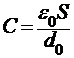 . (2)
. (2)
Здесь S — площадь пластины, ![]() — расстояние между пластинами. Если же объем конденсатора заполнен диэлектриком, то его емкость есть
— расстояние между пластинами. Если же объем конденсатора заполнен диэлектриком, то его емкость есть
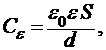 (3)
(3)
где теперь расстояние между пластинами конденсатора определяется толщиной d твердой диэлектрической пластины, диэлектрическая проницаемость которой ![]() .
.
Схема эксперимента.
Работа строится на использовании схем, представленных на рисунках 1 и 2. Здесь С — измерительный конденсатор, R0 — эталонное сопротивление, C0 — эталонный конденсатор, U и U0 — напряжения на измери-
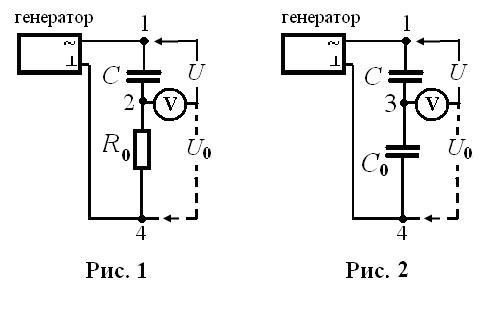
тельном конденсаторе и эталонных элементах R0 и C0 соответственно. Клеммы 1, 2 (рис.1) и 1, 3 (рис.2) служат для поочередного подключения вольтметра к С и R0 (рис.1) или С0 (рис.2). В схеме используется генератор переменного тока частоты ![]() .
.
Особая роль в этой лабораторной работе отводится измерительному плоскому конденсатору С. В первом упражнении, когда конденсатор С является воздушным, а расстояние между его пластинами равно d0, определяется емкость этого конденсатора, причем как в результате теоретического расчета, так и экспериментально (двумя способами).
Во втором упражнении это же устройство заполняют поочередно диэлектрическими пластинами различной толщины 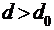 (
(![]() — это и новое расстояние между обкладками), определяют соответствующие значения емкости
— это и новое расстояние между обкладками), определяют соответствующие значения емкости ![]() и диэлектрической проницаемости
и диэлектрической проницаемости ![]() :
:
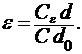 (4)
(4)
Числовые значения постоянных величин d0, R0, C0 и ![]() , входящих в расчетные формулы, даны в таблице 1.
, входящих в расчетные формулы, даны в таблице 1.
|
d0 |
R0 |
С0 |
|
|
1,8 мм |
2,01 кОм |
9,3 нФ |
2,0 кГц |
Таблица 1
Упражнение I
Определение емкости воздушного конденсатора
В данном упражнении сравнивают значение электроемкости воздушного конденсатора, полученное в экспериментах с помощью электрических схем (рис.1 и 2), с рассчитанным теоретически.
Порядок выполнения упражнения
1. В соответствии со схемой, приведённой на рис.1, подсоединить к измерительному конденсатору С эталонное сопротивление R0.
2. Поочередно соединяя штекер вольтметра с клеммами 1 и 4, измерить напряжения U (в В) на измерительном конденсаторе и U0 (в мВ) на эталонном сопротивлении R0. Данные занести в таблицу 2. Измерения повторить 3 раза.
3. Получить средние значения ![]() и
и ![]() и по ним с помощью формулы
и по ним с помощью формулы
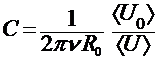 (5)
(5)
и таблицы 1 найти величину С.
4. Используя схему, приведённую на рис.2, подсоединить к конденсатору С эталонный конденсатор С0.
5. Поочередно соединяя штекер вольтметра с клеммами 1 и 4, измерить напряжения U на измерительном конденсаторе и U0 на эталонном конденсаторе. Данные занести в таблицу 2. Измерения повторить 3 раза.
6. Получить средние значения ![]() и
и ![]() и по ним с помощью формулы
и по ним с помощью формулы
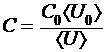 (6)
(6)
и таблицы 1 найти величину С.
7. Измерив с помощью линейки площадь S пластины измерительного конденсатора и используя данные из таблицы I, по формуле (2) рассчитать величину ![]() воздушного конденсатора.
воздушного конденсатора.
8. Сравнить значение ![]() со средним
со средним ![]() , полученным по измерениям на схемах I и II. Вычислить систематическую ошибку опыта:
, полученным по измерениям на схемах I и II. Вычислить систематическую ошибку опыта:
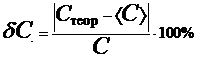
Таблица 2
|
схема |
№ |
U |
|
U0 |
|
C |
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|


