ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ соленоида

6.  Определить удельный заряд по формуле (3). Сравнить резуль­тат со значением в таблице основных физических констант.

Таблица 1

Таблица 2

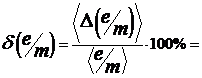
ПРИЛОЖЕНИЕ

Здесь дается вывод формулы (2).

В силу аксиальной (осевой) симметрии задачи (это касается и магнетронной лампы, и конфигурации электрического и магнитного полей) удобно ввести цилиндрическую систему координат 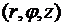с осью z вдоль оси симметрии магнетрона. Декартовы координаты выражаются через цилиндрические 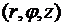формулами (см. рис. 4):

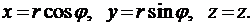
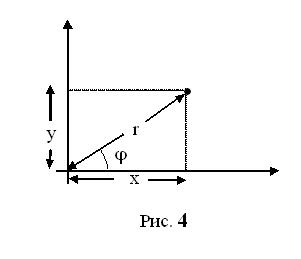При этом цилиндрические компо-ненты векторов скорости, а также кулоновской и лоренцовой сил записыва­ются в виде

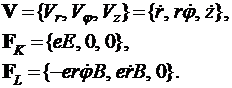(5)

Учитывая, что траектория каждого электрона лежит в плоскости, пер-пендикулярной оси , запишем в проекциях на эту ось уравнение моментов

где L = m [rv] — момент импульса электрона, а M = [r (FK +FL)] — суммарный момент действующих на электрон сил. Будем иметь

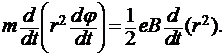(6)

Заметим, что в соответствии с правилами векторного умножения радиальные компоненты векторов (5) в уравнение (6) не вошли.

Интегрирование (6) приводит к «интегралу площадей»

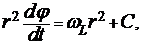(7)

где 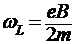— так называемая ларморова частота. Постоянную интегрирования C находим из уравнения (7), полагая в нем, что электрон покидает катод с нулевой начальной скоростью. В частности, при равна нулю угловая скорость . Поэтому 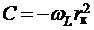. В результате уравнение (7) приобретает вид

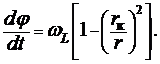(8)

Записывая в цилиндрических координатах закон сохранения механической энергии (1), получаем

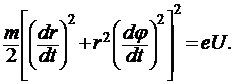
Подставляя сюда (8) и учитывая, что при радиальная компонента скорости электрона на поверхности анода () обращается в нуль, окончательно будем иметь

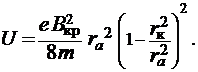
Это и есть формула (2).

Контрольные вопросы

1.  Устройство магнетрона и конфигурация полей в нем.

2.  Как найти величину и направление силы, действующей на электрон в межэлектродном пространстве?

3.  Чем определяется величина скорости электрона в магнетроне?

4.  Как будет двигаться электрон в однородном магнитном поле в отсутствие электрического поля?

5.  Анодный ток и ток соленоида. Зависимость магнитного поля от тока соленоида.

6.  Что означают критические условия в магнетроне? Какие характеристики их описывают?

7.  Как находится в работе критическое значение магнитного поля?

Литература

1. А. В. Астахов, Ю. М. Широков. Курс физики. М.: «Наука», 1980. Т. II. 359 с.

2. И. Е. Иродов. Электромагнетизм. Основные законы. М.-СПб.: Физматлит, 2000. 350 с.

3.  Д. В. Сивухин. Общий курс физики. Т. III. Электричество. М.: «Наука», 1977. 688 с.

4. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1966. Вып. 5. 296 с.

Лабораторная работа Э.5

ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ

СОЛЕНОИДА

Цели работы

1) Определить индукцию магнитного поля внутри соленоида и катушки.

2) Сравнить экспериментальные результаты с расчетом.

Теоретическое введение

Магнитное поле порождается движущимися зарядами и оказывает силовое воздействие на движущиеся заряженные объекты. Упорядоченное движение зарядов называют электрическим током. Таким образом, во-первых, токи создают магнитное поле и, во-вторых, в свою очередь магнитное поле действует на токи. Если сила тока I не изменяется (постоянный ток), то магнитное поле, порожденное таким током, также не изменяется во времени и называется стационарным (в противном случае – переменным).

Одной из основных характеристик магнитного поля является вектор магнитной индукции В (Тл). Вектор В определяет величину и направление силы, с которой магнитное поле действует: а) на любой точечный заряд, движущийся со скоростью v в произвольной точке пространства, где есть магнитное поле:

– так называемая магнитная сила Лоренца;

б) на элемент длины dl линейного проводника (достаточно малого поперечного сечения) с током I:

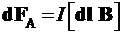– сила Ампера.

Здесь вектор dl направлен вдоль провода в направлении тока, квадратными скобками обозначено векторное произведение заключенных в них сомножителей.

Закон Био – Cавара позволяет рассчитать величину и направление вектора индукции магнитного поля, созданного элементом тока в произвольной точке пространства на расстоянии r от тока: