Методичка по решению задач по статике
Б2.В.2 ОПД. Ф.02.01 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
МЕТОДИЧЕСКОЕ УКАЗАНИЕ
по решению задач по статике
Направление подготовки бакалавра 110800 Агроинженерия
Профили:
Технические системы в агробизнесе;
Технический сервис в агропромышленном комплексе;
Электрооборудование и электротехнологии.
Направление подготовки бакалавра 140100 Теплотехника и теплоэнергетика
Профиль
Энергообеспечение предприятий
УФА 2011
УДК 539.3
ББК 30.121
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства (протокол № 11 от 25.05.2011 г.)
Ответственный за выпуск: заведующий кафедрой “Теоретическая и прикладная механика”, к. т.н. доцент Масалимов И. Х.
1 Настоящая методическая разработка содержит указания по решению задачи по статике на равновесие тела под действием произвольной плоской системы сил. Условия задачи даны в задачнике /1/.
2 Прежде чем приступить к решению задачи, необходимо изучить теоретический материал в §§ 3, 5, 13, 16, 18 /2/. Разберите также примеры, приведенные в §17. Обратите внимание на определение равнодействующей распределенной системы сил в §21 /2/.
3 Вопросы для самоконтроля.
3.1 Что называется связью, реакцией связи?
3.2 Какие связи называются внутренними?
3.3 Что называется интенсивностью распределенной нагрузки?
3.4 Как определяется положение точки приложения равнодействующей распределенной нагрузки?
3.5 В чем смысл применения третьего закона Ньютона при рассмотрения составных конструкций?
3.6 Как определяется момент равнодействующей силы относительно любой точки по теореме Вариньона?
4 Указания к решению задачи.
Задача заключается в анализе равновесия системе двух тел под действием плоской системы сил. При ее решении можно рассмотреть сначала равновесие всей системы в целом, а затем равновесие одного из тел системы, изобразив его отдельно и заменив действие другого тела его реакциями. Чаше, однако, сразу расчленяют систему и рассматривают равновесие каждого из тел в отдельности, применяя при этом закон о равенстве действия и противодействия.
5 Указания по использованию ЭВМ
В задачах требуется найти точку приложения и направления силы ![]() 2 на указанном в таблице участке составной конструкции, при котором указанная составляющая реакция связи в точке В имеет максимальное или минимальное значение. Задачи оптимизации требуют многовариантных расчетов с использованием ЭВМ. Общая методика при этом следующая. Из аналитических уравнений равновесия составляются выражения для указанной в условиях составляющей реакции связи в точке В в зависимости от значений z и направляющего угла β или γ. Определение экстремальных значений этих параметров производится с применением ЭВМ. При расчетах значение z и β(γ) рекомендуется изменять с шагами 0,01 м и 1º соответственно. Из множества вариантов машина выделяет тот, при котором составляющая реакции связи имеет максимальное (минимальное) значение.
2 на указанном в таблице участке составной конструкции, при котором указанная составляющая реакция связи в точке В имеет максимальное или минимальное значение. Задачи оптимизации требуют многовариантных расчетов с использованием ЭВМ. Общая методика при этом следующая. Из аналитических уравнений равновесия составляются выражения для указанной в условиях составляющей реакции связи в точке В в зависимости от значений z и направляющего угла β или γ. Определение экстремальных значений этих параметров производится с применением ЭВМ. При расчетах значение z и β(γ) рекомендуется изменять с шагами 0,01 м и 1º соответственно. Из множества вариантов машина выделяет тот, при котором составляющая реакции связи имеет максимальное (минимальное) значение.
6. Пример 1
6.1 Найти точку приложения и направления силы ![]() 2 на участке АВ составной конструкции (рисунок 6.1), при которых реактивный момент заделки в точке В имеет минимальное значение.
2 на участке АВ составной конструкции (рисунок 6.1), при которых реактивный момент заделки в точке В имеет минимальное значение.
При найденных значениях z и направляющего угла γ определить реакции опор и усилие в промежуточном шарнире С.
Дано: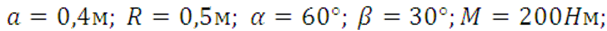
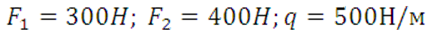
6.2 Решение
Действие равномерно распределенной нагрузки интенсивности q заменяем равнодействующей
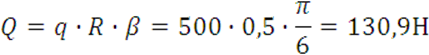
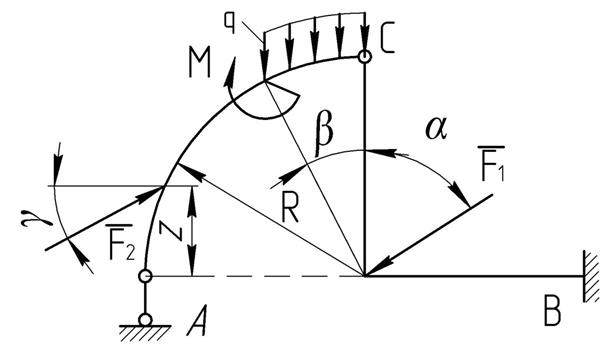
Рисунок 6.1 Составная конструкция
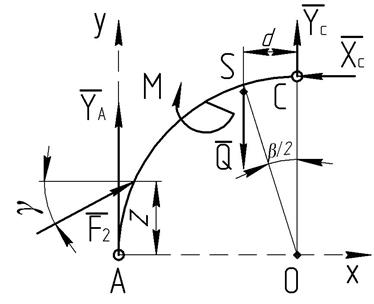
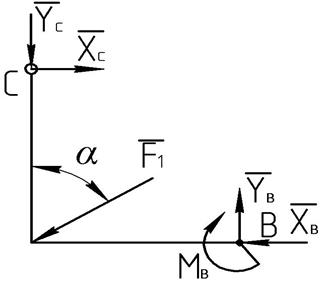
Рисунок 6.2 Рисунок 6.3
Равновесие левой части Равновесие правой части
Равнодействующую Q прикладываем к точке S – центр тяжести дуги окружности.
![]()
Плечо равнодействующей относительно шарнира С равно
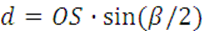
Рассмотрим равновесие части АС составной конструкции. Заменим действие опоры А реакцией ![]() (рисунок 6.2), реакцию цилиндрического шарнира С показываем двумя составляющими —
(рисунок 6.2), реакцию цилиндрического шарнира С показываем двумя составляющими — ![]() и
и ![]() .
.
Аналитические условия равновесия произвольной плоской системы сил:
ΣX=0, ΣY=0, ΣmA=0.
В развернутом виде:
ΣX=F2·cosγ-XC=0, (1)
ΣY=YA+ F2·sinγ-Q+YC=0, (2)
ΣmA=- F2·cosγ·z+ F2·sinγ·(R-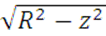 )-M-Q·(R-d)+XC·R+YC·R=0. (3)
)-M-Q·(R-d)+XC·R+YC·R=0. (3)
Рассмотрим равновесие части ВС конструкции (рисунок 6.3). действие в заделки точки В заменим составляющими ![]() и
и ![]() и реактивным моментом МВ. Учитывая закон равновесия действия и противодействия, составляющие
и реактивным моментом МВ. Учитывая закон равновесия действия и противодействия, составляющие ![]() и
и ![]() направим в стороны, противоположные направлениям на рисунке 6.1.
направим в стороны, противоположные направлениям на рисунке 6.1.
Общее условие равновесия:
ΣX=0, ΣY=0, ΣmВ=0.
ΣX=XC-XB-F1·sinα=0, (4)
ΣY=YB — YC — F1·cosα =0, (5)
ΣmB=-XC·R+YC·a+F1·cosα-MB=0. (6)
Из уравнения равновесия (1-6) находим:
XC= F2·cosγ, (7)
YC=(F2·cosγ·z-F2·sinγ·(R-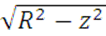 )+M+Q·(R-d)-XC·R)/R, (8)
)+M+Q·(R-d)-XC·R)/R, (8)
YA= — F2·sinγ+Q-YC, (9)
XB=XC-F1·sinα, (10)
YB =YC+ F1·cosα, (11)
MB= — XC·R+YC·a+F1·cosα. (12)
Таким образом, пользуясь формулами (7), (8) и (12), можно определить реактивный момент заделки МВ в зависимости от параметров z и γ. Составим программу для оптимизации на алгоритмическом языке «Паскаль».
program statica
var q, OS, d,z, mbmin, zmin, tmin, xc, yc,
xb, yb, mb:real;
i, t:integer;
const a=0,4;r=0,5;v=60;u=30;m=200;f1=300;
f2=400;g1=500;
begin
mbmin:=10000;
q:=q1*r*u*pi/180;
OS:=r*sin(u*pi/360)/(u*pi/360);
d:=r*sin(u*pi/360);
for t:=0 to 360 do
begin
for i:=0 to trunc(r/0,01) do
begin
z:=i*0,01;
xc:=f2*cos(t*pi/180);
yc:=(f2*cos(t*pi/180)*z-f2*(r-sqrt(r*r —
-z*x))*sin(t*pi/180)+m+q*(r-d)-xc*r)/r;
mb:=f1*a*cos(v*pi/180)+yc*a-xc*r;
if abs(mb)<abs(mbmin) then
begin
mbmin:=mb;zmin:=z;tmin:=t;
end;
end;
end;
writeln(‘mbmin’,’=’,mbmin:3:3);
writeln(‘zbmin’,’=’,zbmin:3:3);
writeln(‘tbmin’,’=’,tbmin:3:3);
end.
Примечание. В программе начальное значение МВmin принято произвольно 10000 (заведомо больше, чем действительное).
Угол α обозначен v, угол β-u,γ-t.
В результате вычислений на ЭВМ получены следующие результаты:
МВmin=-0,020Н·м при z=0,230м и γ=338°
По формулам (7-11) производим подсчеты остальных реакций связей:
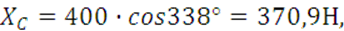
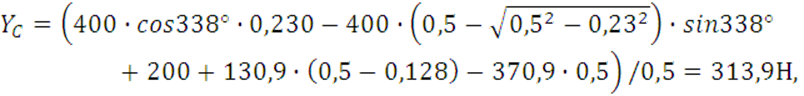
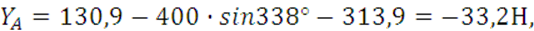
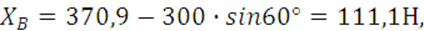
![]()
Действительное направление вектора ![]() противоположно показанному на чертеже.
противоположно показанному на чертеже.
7 Пример 2.
7.1 Найти точку приложения и направление силы ![]() на участке ЕF составной конструкции (рисунок 7.1), при которой реакция опоры В имеет наибольшее значение.
на участке ЕF составной конструкции (рисунок 7.1), при которой реакция опоры В имеет наибольшее значение.
Дано: a=0,4м, ℓ1=0,3м, ℓ2= 0,6м, ℓ3= 0,7м, ℓ4= 0,7м, 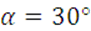 ,
,
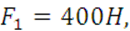
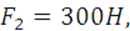
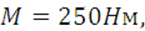
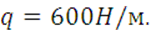
7.2 Решение
Равнодействующая равномерно распределённой нагрузки равна
Q= ![]() ℓ1
ℓ1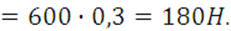
Расчленим систему по шарниру С и рассмотрим равновесие балки СD
(рис.7.2). Реакция ![]() перпендикулярна опорной поверхности подвижной опоры D, реакцию цилиндрического шарнира С показываем двумя составляющими
перпендикулярна опорной поверхности подвижной опоры D, реакцию цилиндрического шарнира С показываем двумя составляющими ![]() и
и ![]() .
.
Аналитические условия равновесия плоской системы сил записываются:
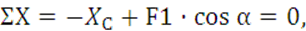 (13)
(13)
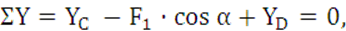 (14)
(14)
 (15)
(15)
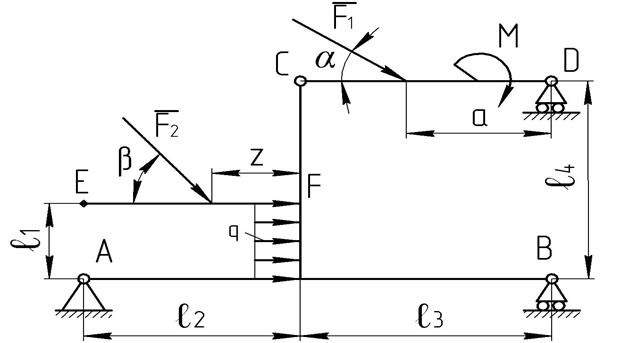
Рисунок 7.1 Составная конструкция
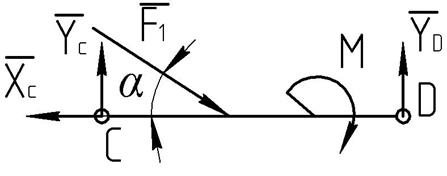
Рисунок 7.2 Равновесие правой части
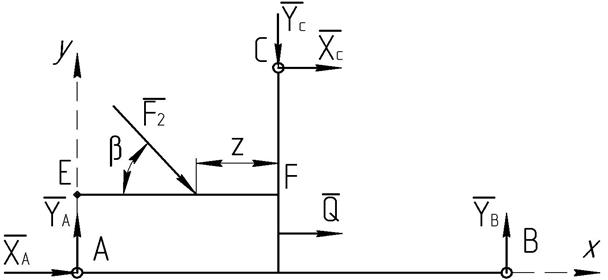
Рисунок 7.3 Равновесие левой части
Рассматриваем равновесие оставшейся части составной конструкции (рисунок 7.3). Показываем на чертеже реакцию ![]() подвижной опоры В и составляющие
подвижной опоры В и составляющие ![]() и
и ![]() реакции в шарнире С показываем в стороны, противоположные направлениям на рисунок 7.2.
реакции в шарнире С показываем в стороны, противоположные направлениям на рисунок 7.2.
Условия равновесия будут иметь вид:
ΣX=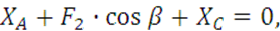 (16)
(16)
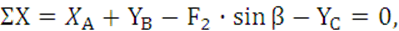 (17)
(17)
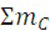 =
=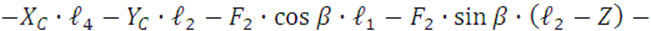
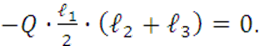 (18)
(18)
Из уравнений равновесия (1-6) находим:
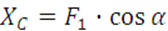 , (7)
, (7)
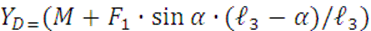 , (8)
, (8)
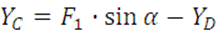 , (9)
, (9)
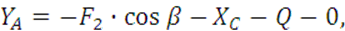 (10)
(10)
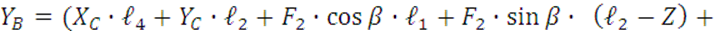
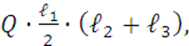 (11)
(11)
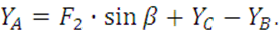 (12)
(12)
Пользуясь последовательно формулами (7), (8), (9) и (11), можно найти реакцию ![]() максимальное значение которой необходимо определить.
максимальное значение которой необходимо определить.
Составляем программу на алгоритмическом языке “БЕЙСИК”.
1![]() INPUT F1, F2, m,
INPUT F1, F2, m, ![]() 1
1
2![]() INPUT
INPUT ![]() , L1, L2, L3, L4
, L1, L2, L3, L4
3![]() INPUT V.
INPUT V.
4![]() INPUT 3.1416*V/18
INPUT 3.1416*V/18![]()
5![]()
![]() 2=
2=![]() 1*L1
1*L1
6![]()
![]() =
= ![]()
7![]() FOR t=
FOR t=![]() to 2*3.1416 step 3.1416/180
to 2*3.1416 step 3.1416/180![]()
8![]() FOR Z=
FOR Z=![]() to L2 step
to L2 step ![]() .
.![]()
9![]() XC=F1*cos (S)
XC=F1*cos (S)
10![]() YB=(m+F1*sin(S)*(L3-
YB=(m+F1*sin(S)*(L3-![]() ))/L3
))/L3
11![]() YC=F1*sin (S)-YD
YC=F1*sin (S)-YD
12![]() (XC*L4+YC*L2+F2*cos(t)*L1+F2*sin(t)*(L2-Z)+
(XC*L4+YC*L2+F2*cos(t)*L1+F2*sin(t)*(L2-Z)+ ![]() 2*(L1/2)/L2+L3
2*(L1/2)/L2+L3
13![]() IF ABC (YB)
IF ABC (YB)![]() =d THEN GOTO15
=d THEN GOTO15![]()
14![]() d= YB:e=t*57.325:
d= YB:e=t*57.325:![]() =Z
=Z
15![]() NEXTZ
NEXTZ
16![]() NEXTt
NEXTt
17![]() PRINT d; e;
PRINT d; e; ![]()
Примечание к программе. Максимальное значение ![]() обозначено d и. в начале, принято равным нулю. Экстремальные значения z и
обозначено d и. в начале, принято равным нулю. Экстремальные значения z и ![]() обозначены соответственно е и
обозначены соответственно е и ![]() .
.
Получаем: 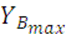 = 221,6H при
= 221,6H при ![]() =
=![]() и Z=0.
и Z=0.
8 БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Курс теоретической механики : учебник для вузов / А. А. Яблонский, В. М. Никифорова. – М.: Кнорус, 2010. — 597 с.
2. Бутенин, Н. В. Курс теоретической механики [Текст] : в 2 т. : учеб. пособие для студ. вузов, обуч. по техн. спец. / Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин. — Изд. 9-е, стер. — СПб. ; М. ; Краснодар : Лань, 2007. — (Учебники для вузов. Специальная литература) Т. 1 : Статика и кинематика, Т. 2 : Динамика. – 2007. – 239 с
3. Сборник заданий для курсовых работ по теоретической механике [Текст] : учеб. пособие для студ. вузов : допущено М-вом высшего и среднего специального образования СССР / [А. А. Яблонский и др.]; под общ. ред. А. А. Яблонского. — 17-е изд., стер. — М. : Кнорус,2010. – 382 с.
Конспект лекций по теоретической механике


