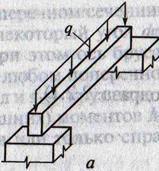
Модуль упругости при сдвиге g

4. Поэтому часто сдвиг называют срезом.

Модуль упругости при сдвиге G

1. Зависит от модуля упругости I рода Е

G = E2(1 + µ)

µ — коэффициент Пуассона

2. Пример, для стали 30 Е = 2∙105 Нмм2 2∙105 2(1 + 0,3) = 0,77∙105 Нмм2

3. Сдвиг – это напряжённое состояние. Если деформации от сдвига находятся в пределах упругости, то после снятия нагрузки размеры и форма детали восстанавливаются – упругие деформации.

4. Если превышен предел упругости, происходят пластические деформации.

4. Формула для расчёта напряжения сдвига (среза)

τср = Q Sср

Условие прочности при расчёте на срез

τср = Q Sср[τср]

τср – расчётное напряжение среза в поперечном сечении детали

Q – поперечная сила в сечении Q = Fi

i – число соединительных деталей

Sср – площадь среза

[τср] – допускаемое напряжение при расчёте на срез (зависит от материала и условий работы)

Виды расчётов из условий прочности

1. Проверочный.

2. Проектный – определение числа соединительных деталей при заданных размерах или определение размеров детали при заданном их числе.

3. Определение допускаемой нагрузки.

Смятие

1. При сжатии двух тел возникает опасность смятия контактирующих поверхностей.

2. Напряжение смятия – напряжение, возникающее при сжатии двух контактирующих поверхностей.

3. Пример смятия: клёпаные и болтовые соединения.

4. Формула для расчёта напряжения смятия

σсм = FSсм

5. Условие прочности на смятие

σсм = FSсм [σсм]

F – сила, с которой сдавливаются контактирующие поверхности

Sсм – площадь смятия

5. Если поверхность смятия криволинейная, то Sсм = S поверхности этой поверхности на плоскость, перпендикулярную линии действия сминающей силы.

6. Расчёты на смятии носят условный характер: считают, что силы давления распределены по поверхности смятия равномерно и перпендикулярны ей.

Самостоятельная работа обучающихся (эзс – 1 час, арх – 2 час, авто – нет)

1. Выполнить чертёж для демонстрации закона Гука при сдвиге и сделать к нему краткое описание

ТЕМА 2.4.ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ(4.4. – АВТО)

(эзс – 2 час, арх – 1 час, авто – 1)

Моменты инерции сечений

1. Статический момент инерции — алгебраическая сумма произведений элементарных площадей на координаты их центров тяжести – мм3 , см3 , м3

(сумма d S ∙ х или d S ∙ у)

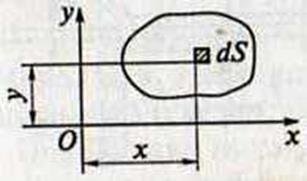
а) в интегральной форме

Sх = ∫ уdS — статический момент инерции относительно оси х

Sу = ∫ хdS — статический момент инерции относительно оси у

б) по формулам статики Sх = Syс Sу = Sхс

S – площадь сечения

yс и хс – координаты центра тяжести сечения

в) если ось х проходит через центр тяжести сечения → yс = 0→ Sх = Syс = S∙0 = 0

г) статические моменты сечения относительно центральных осей равны нулю (центральные оси – проходят через центр тяжести сечения – так как yс = 0 и хс = 0)

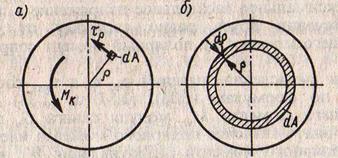
2. Полярный момент инерции — сумма произведений площадей элементарных площадок поперечного сечения на квадраты их расстояний от центра (для круглого сечения – мм4 , см4 , м4)

Jр = ∫p2dS

S

р – расстояние от центра до центра тяжести элементарной площадки.

3. Осевые моменты инерции относительно координатных осей х и у.

а) представим, что сечение разделено на множество элементарных площадок dS

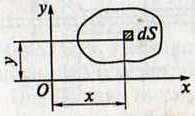
б) координаты элементарной площадки х и у.

в) тогда интегралы

Jх = ∫у2dS и Jу = ∫х2dS

S S

называются моментами инерции сечения относительно осей х или у

4. Центробежные моменты инерции относительно координатных осей х и у.

Jху = ∫хуdS

S

5. Связь между осевыми моментами инерции относительно парал­лельных осей

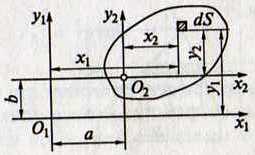
а) введём две системы координат О1х1у1 и О2х2у2 – оси которых попарно параллельны и находятся на расстоянии а и b

б) система О2х2у2 – связана с телом

в) х2 = х1 – а у2 = у1 – b

г) определение статического момента сечения относительно оси х2

Sх2 = ∫( у1 – b)dS = ∫у1dS — ∫bdS

S S S

Sх2 = Sх1 — bS

д) определение статического момента сечения относительно оси у2

Sу2 = ∫( х1 – а)dS = ∫х1dS — ∫аdS

S S S

Sу2 = Sу1 — аS

Вывод: при параллельном переносе осей статический момент меняется на величину, равную произведению площади S на расстояние между ними (осями)

6. Всегда можно ( единственный вариант) подобрать оси так, чтобы

А) Sх1 – bS = 0- (центр тяжести лежит на оси х1→ у1 = 0, b = 0→ Sх1= ∫у1dS = 0→ bS = 0

s

Б). Sу1 — аS= 0

(центр тяжести лежит на оси у1→ х1 = 0, а = 0→ Sу1= ∫х1dS = 0→ аS = 0

7. Вывод:

А) центральная ось — ось, относительно которой статический момент равен нулю.

Б) центр тяжести сечения – точка пересечения центральных осей

В) статический момент относительно всякой оси, проходящей через центр тяжести, равен нулю.

8. Расстояние до центральных осей от произвольно взятых определяется зависимостями

Из Sх = Syс Sу = Sхс → Ус = Sх1S Xс = Sу1S

10. Понятие о главных центральных моментах инерции

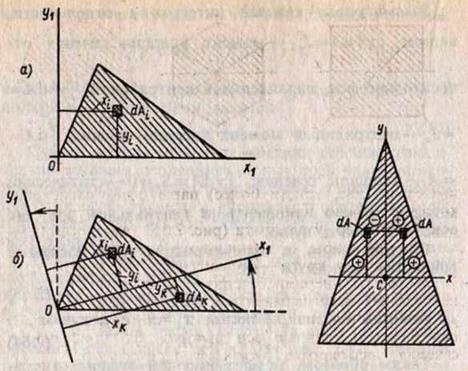
А) главные оси – оси, относительно которых осевые моменты инерции принимают экстремальные значения, а центробежный момент равен нулю.

Б) практическое значение имеют не любые главные оси, а только главные центральные оси (через центр тяжести)

В) сечение с двумя осями симметрии (например, прямоугольник) имеет две главные центральные оси симметрии (центральные → проходят через центр тяжести, главные →

— по одну сторону от оси площадка dS (dA) с элементарным моментом инерции + хуdA (так же, как у треугольника)

— по другую сторону от — хуdA

— при суммировании их по всему сечению Jху = 0

— осевые моменты сечения экстремальные: относительно оси у — произведение площади на координату х)

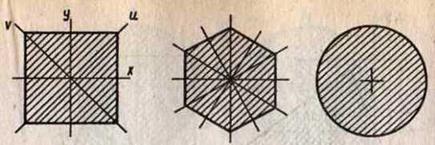
Г) у квадрата две пары две пары центральных главных осей

Д) у правильного шестиугольника три пары центральных главных осей

Е) у круга – бесчисленное множество пар

Ж) главные центральные моменты инерции – моменты инерции сечения относительно главных центральных осей.

З) главные плоскости – плоскости, проведённые через ось бруса и главные оси инерции его поперечного сечения.

Самостоятельная работа обучающихся (эзс – 2 час, арх – 4 час, авто – 2)

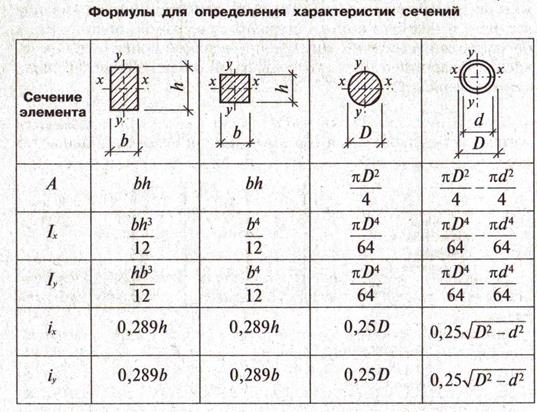
1. Заполнить таблицу основных геометрических характеристик для наиболее

распространенных форм сечений и вложить их в «Приложения».

2. Решить задачи по определению центра тяжести и геометрических характеристик сложных фигур

1. Решение задач на определение главных центральных момен­тов инерции составных сечений, имеющих ось симметрии — авто

ТЕМА 2.5. ПОПЕРЕЧНЫЙ ИЗГИБ ПРЯМОГО БРУСА(4.5. – АВТО)

(эзс – 6 час, арх – 4 час, авто – 6)

Основные понятия и определения

1. Изгиб – вид нагружения, при котором в поперечных сечения бруса возникают изгибающие моменты, прямолинейная ось бруса искривляется;

2. Классификация видов изгиба

А) продольный (колонны) и поперечный: прямой и косой

Б) простой (прямой, чистый) или сложный

3. Наиболее распространённая конструкция, работающая на изгиб – балка (брус, работающий на изгиб)

4. Если изгибающий момент является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, то такой изгиб называется чистым;

5. Простейший случай изгиба балки — плоский поперечный изгиб;

6. Изгиб называется плоским, если поперечное сечение балки симметрично относительно вертикальной оси и действующие нагрузки расположены в плоскости сечения;

7. Если при этом все нагрузки вертикальные, то изгиб называется плоским поперечным;