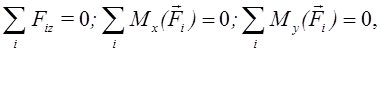Момент силы относительно точки и оси

– для произвольной системы сил.

– для плоской системы сходящихся сил.

1.5. Момент силы относительно точки и оси

1.  Алгебраический момент силы относительно точки.

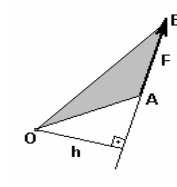
Используется при рассмотрении плоской системы сил. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис.10). Плечом h силы F называют кратчайшее расстояние между этой точкой и линией действия силы. Знак зависит от направления "вращения" тела относительно точки: при "вращении" тела против часовой стрелки будем считать момент положительным МО — (+) и наоборот МО — (-).

;

.

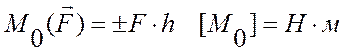
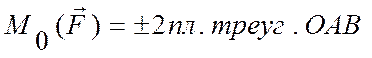
Рис. 10

2. Векторный момент силы относительно точки.

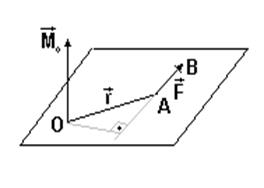Векторным моментом силы относительно точки называют вектор приложенный в этой точке и равный по модулю (рис.11), произведению силы на плечо силы относительно этой точки. Векторный момент направлен перпендикулярно плоскости, в которой лежат сила и точка, таким образом, что с его конца можно видеть "стремление" силы вращать тело против движения часовой стрелки.

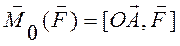
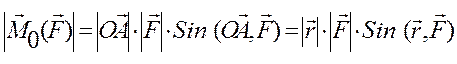
Рис. 11

Векторный момент силы относительно точки не меняется при скольжении силы по линии действия и равен нулю, если линия проходит через точку О.

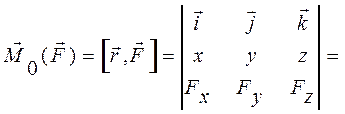
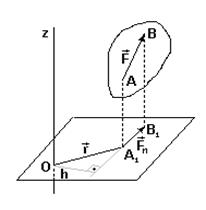
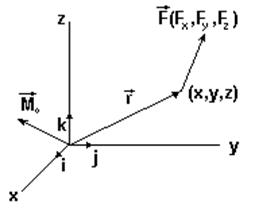Момент силы относительно начала координат можно выразить через проекции силы на координатные оси и координаты точки приложения силы (рис.12).

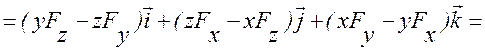
Рис. 12

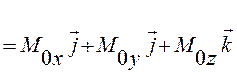
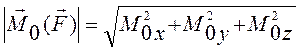
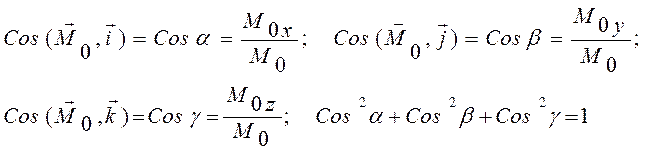
3. Момент силы относительно оси.

Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси (рис.13), относительно точки пересечения оси с этой плоскостью.

Знак определяется направлением вращения (против часовой стрелки − (+), по часовой стрелки − (−)).

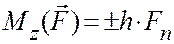
Рис. 13

Замечания: а) Mz=0, если сила параллельна оси Oz.

б) Mz=0, если линия действия пересекает ось Oz.

Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

1.6. Приведение системы сил к простейшей системе

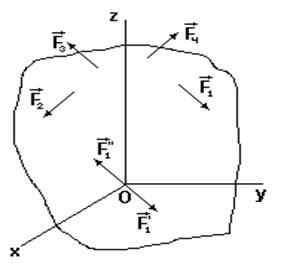Пусть на тело действует произвольная система сил 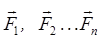. Приве­дем эту систему сил к заданному центру. Выберем произвольную точку О за точку приведения (рис.14).

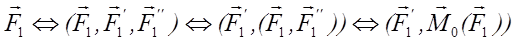Рассмотрим одну из сил системы – F1. Добавим в точке О нулевую систему сил – (F1′, F2"). Заметим, что силы (F1, F1") представляют пару сил, которую можно заменить вектором момента пары

Рис.14

M0 (F1), приложенным в точке О (он же равен мо-менту силы F1 относительно центра О), то есть исходная сила эквилентна силе F1′ и вектору момента пары, приложенным в той же точке.

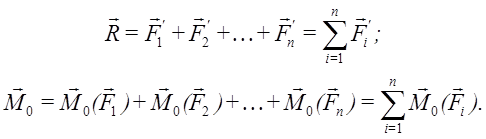Проведя аналогичную операцию со всеми векторами исходной системы сил, мы получим два пучка векторов, приложенных в точке O – пучок сил 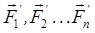и пучок векторов моментов 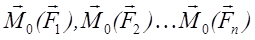которые приводятся к эквивалентной системе двух векторов:

Главным вектором системы сил называют вектор, равный векторной сумме этих сил (вектор R). Значение главного вектора сил не зависит от выбора точки приведения.

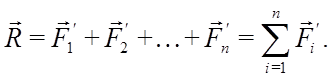
Главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относи­тельно этой точки (вектор момента результирующей пары М0). Вектор М0 зависит от точки приведения О:

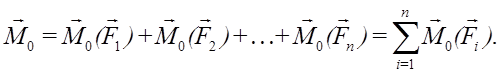
По проекциям сил можно найти модуль главного вектора и главного момента, а также косинусы их углов с осями координат.

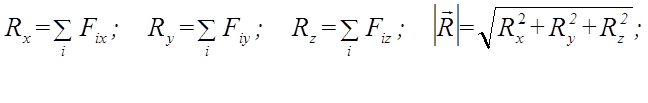
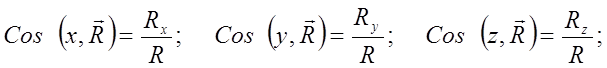
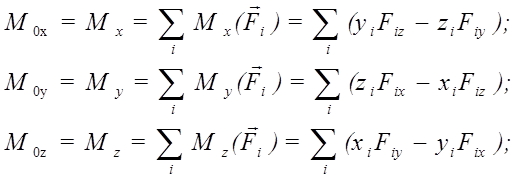
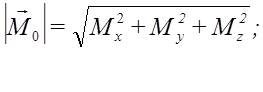
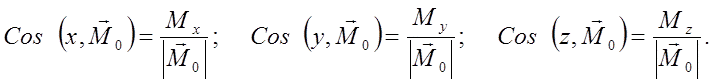
Главный момент плоской системы сил перпендикулярен главно­му вектору.

1.7. Условия равновесия систем сил

Пространственная система сил

Если система сил находится в равновесии, то в равновесии нахо­дится и эквивалентная ей система, состоящая из главного вектора и главного момента пары. Чтобы такая система сил была эквивалентна нулю, необходимо и достаточно, чтобы выполнялось условие: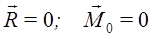 ( где О – произвольная точка)

Эти условия являются векторными условиями равновесия для любой системы сил. В аналитической форме это эквивалентно усло­виям: Rx=Ry=Rz=0; Mx=My=Mz=0,

то есть в самом общем случае имеем шесть скалярных уравнений равновесия (уравнений статики).

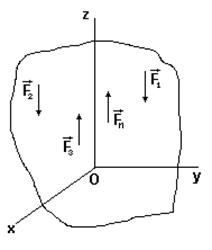
Система параллельных сил (рис. 15)

Пусть Fi параллельно оси Oz, тогда

Mz тождественно равно нулю и

.

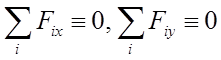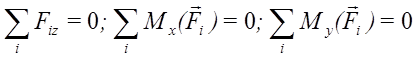Таким образом, имеем три уравнения равновесия

Рис.15

Плоская система сил (рис. 16)

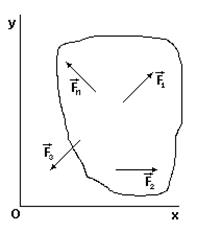После отбрасывания тождеств: