динамическая планетарная модель атомов

На основе своих опытов по рассеянию α-частиц Э. Резерфорд в 1911 г. предложил динамическую планетарную модель атомов, где электроны движутся по круговым орбитам вокруг ядра, в котором сосредоточена почти вся масса атома. Дальнейшее развитие представлений о строении атомного ядра связано с открытием изотопов, связи между порядковым номером химического элемента в периодической системе элементов Менделеева и электрическим зарядом ядра, открытием положительно заряженного протона (Э. Резерфорд, 1919 г. ) и электрически нейтрального нейтрона (Дж. Чедвик, 1932 г.). Согласно современным представлениям атомное ядро состоит из протонов и нейтронов, связанных сильным взаимодействием, имеет размеры порядка м, причем радиус R ядра растет с увеличением числа А нуклонов в ядре как А1/3.

Простейшим атомом является атом водорода, образованный из протона и электрона. Поскольку масса протона 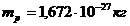много больше массы электрона , то в первом приближении можно считать, что в планетарной модели электрон движется по круговой орбите вокруг неподвижного протона. Согласно второму закону Ньютона для электрона водорода выполняется уравнение движения в виде

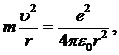(10.1)

где – линейная скорость электрона, r – радиус круговой орбиты, +e – заряд протона.

Кулоновская сила взаимодействия зарядов является консервативной и центральной, поэтому для замкнутой системы в виде протона и электрона без учета излучения выполняются законы сохранения механической энергии Е

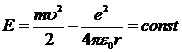(10.2)

и момента импульса электрона, который в данном случае может быть записан в виде

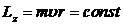. (10.3)

Здесь — проекция момента импульса на ось z, проходящей через центр круговой орбиты перпендикулярно ее плоскости.

Исключая из уравнений (10.2) – (10.3) скорость , получим, что энергия атома

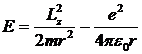. (10.4)

Если для устойчивости состояния потребовать минимум энергии атома и положить

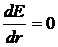, (10.5)

то приходим к следующим выражениям для радиуса круговой орбиты и энергии атома:

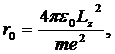
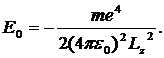(10.6)

Величины и остаются неопределенными, поскольку неизвестно значение .

Необходимо учесть, что движущийся по круговой орбите электрон обладает центростремительным ускорением и согласно законам классической электродинамики должен излучать электромагнитные волны, теряя при этом свою энергию. Скорость потерь энергии описывается классическим выражением для излучения электрического диполя

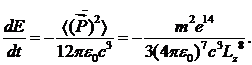(10.7)

Используя соотношение (10.6) между и , получим

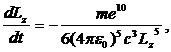(10.8)

где

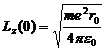(10.9)

— начальное значение проекции момента импульса электрона, находящегося на круговой орбите радиусом .

Решение уравнения (10.9) дает, что за время

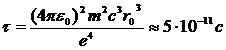(10.10)

величина обращается в нуль, т. е. электрон упадет на протон. Здесь принято, что 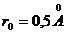(радиус атома водорода в основном состоянии). В процессе падения частота обращения электрона вокруг протона, как следует из (10.3) и (10.4), неограниченно растет пропорционально .

При падении электрона на протон должны излучаться электромагнитные волны сплошного спектра с частотами 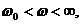равными частотам обращения электрона вокруг протона. Здесь — минимальная частота, равная угловой скорости электрона на исходной орбите. Однако опыт показывает что атомы в основных состояниях стабильны, а их излучение имеет линейчатый спектр, т. е. состоит из отдельных электромагнитных волн с определенными дискретными частотами. Частоты электромагнитных волн, излучаемых атомом водорода, могут быть сгруппированы в определенные серии. Еще в XIX веке была хорошо изучена серия Бальмера (И. Бальмер, 1885 г.), относящаяся к видимой области спектра, длины волн которой описываются простой формулой

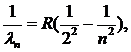n= 3,4,5,… , (10.11)

где 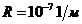— постоянная Ридберга.

Таким образом, классическая физика на основе планетарной модели не смогла объяснить ни стабильность атомов, ни линейчатый спектр их излучения. Возникшие трудности были решены Н. Бором в 1913 г., который сформулировал два постулата, выражающие обобщение опытных данных. Эти постулаты, радикально изменившие представления о состояниях частицы и процессах изменения ее состояний, не могут быть выведены из опыта логическим путём.

Экспериментальные и теоретические исследования взаимодействия электромагнитных волн с веществом показали необходимость принятия гипотез о квантовании энергии вещественного гармонического осциллятора, а также энергии и импульса электромагнитных волн. Перенос идеи квантования на динамические переменные частиц веществ, к которым относятся импульс, момент импульса и энергия, оказался плодотворным в понимании строения атомов и их взаимодействия с электромагнитным излучением.

Согласно первому постулату Бора существуют особые состояния электрона, называемые стационарными, в которых его энергия не меняется во времени несмотря на ускоренное движение. В этих стационарных состояниях проекция момента импульса электрона на заданное направление квантуется и описывается формулой