Напряжения в наклонных сечениях при растяжении

.

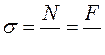В окрестности какой-либо точки S, лежащей в плоскости сечения abb′a′ (рис. 29), выделим бесконечно малый элемент (рис. 30а). Поскольку на грани, перпендикулярной к направлению растягивающей силы, действует нормальное напряжение , а на остальных гранях напряжения отсутствуют, то элемент находится в линейном напряжённом состоянии (главные напряжения, 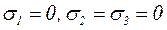). Условимся такой элемент изображать в виде плоской фигуры (рис. 30б), хотя в действительности он имеет форму прямоугольного параллелепипеда.

Определим напряжение, возникающее в наклонном сечении a1b1b1′a1′(рис. 30а, б), перпендикулярном к плоскости рисунка. Положение наклонной площадки определяется углом α между направлением главного вектора и внешней нормалью n−n к площадке. Этот угол считают положительным, если его отсчитывают против часовой стрелки от направления . Наклонную площадку обозначают углом, определяющим её положение. Так, для принятого на рис. 6.3б обозначения угла имеем α-площадку (площадка a1b1). На этой площадке будут действовать нормальное, σα и касательное τα напряжения, для определения которых применяют метод сечений. Так как наклонная площадка рассекла элемент на две части, отбросим одну из них (например, верхнюю) и рассмотрим равновесие оставшейся (нижней) части (рис. 30в). Условие равновесия запишем в виде проекций всех сил на нормаль n−n и площадку t−t:

;

где – площадь наклонного сечения.

Учитывая, что 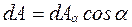, из уравнений равновесия находим:

(6.1)

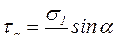. (6.2)

Для определения напряжений на площадке, перпендикулярной к площадке a1b1 (рис. 30г), расположенной под углом (), заменим в формулах (6.1) и (6.2) угол α на (), получим:

; (6.3)

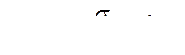. (6.4)

Для направлений напряжений σ и τ, действующих по наклонным площадкам, принимаем следующее правило знаков: нормальное напряжение положительно, если оно растягивающее; касательное напряжение положительно, если для совпадения с его направлением нормаль к площадке необходимо повернуть по направлению движения часовой стрелки.

Отметим некоторые свойства линейного напряжённого состояния, вытекающие из зависимостей (6.1)–(6.4):

1. Сумма нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам, постоянна и равна главному напряжению, т. е.

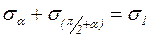. (6.5)

Этим свойством нормальных напряжений обычно пользуются для проверки правильности их вычислений.

2. На двух взаимно перпендикулярных площадках касательные напряжения равны, но противоположны по знаку, т. е.

. (6.6)

Данное свойство является общим для любого напряжённого состояния (закон парности касательных напряжений).

3. Величина нормального напряжения в любом наклонном сечении (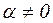) меньше и достигает максимума лишь в поперечных сечениях ().

4. Касательное напряжение наибольшее значение имеет в сечении, составляющем угол 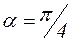с направлением . В этом случае

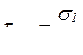. (6.7)

Оценивая напряжённое состояние стержня при его осевом растяжении или сжатии, можно сделать заключение о том, что стержень разрушается либо по поперечному сечению в результате действия максимальных нормальных напряжений, либо по наклонной (под углом 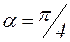) плоскости от действия наибольших касательных напряжений.

6.3. Напряжения в наклонных сечениях при растяжении

в двух направлениях

Рассмотрим общий случай плоского (двухосного) напряжённого состояния, когда отличны от нуля два главных напряжения и (рис. 32а). Между направлением напряжения и площадкой угол равен Из условия равновесия отсечённой правой части (рис. 32б) определим напряжения и . Для этого воспользуемся уравнениями (6.1) и (6.2). Суммируя напряжения от действия с напряжением от действия (заменяя угол α на угол (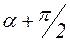)), получим:

,

откуда

. (6.8)