Напряжённо-деформированное состояние балки
Напряжённо-деформированное состояние балки при прямом поперечном изгибе
Внешние нагрузки.
1. В простейшем случае прямого изгиба балки внешние нагрузки действуют в одной (вертикальной) плоскости перпендикулярно оси балки.
2. На балку могут действовать силы:
А) сосредоточенные
Б) распределённые по длине (встречаются в строительстве чаще)
В) изгибающие моменты
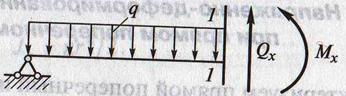
Анализ внутренних силовых факторов начинается с определения полной системы внешних сил.
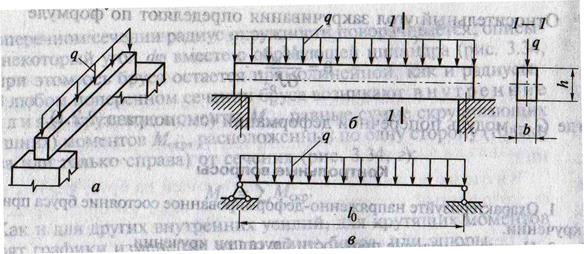
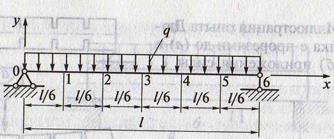
3. Рассмотрим горизонтальную балку прямоугольного сечения на двух опорах и загруженную равномерно распределённой вертикальной нагрузкой q.
4. Поперечное сечение балки имеет высоту h
5. Если балка опирается на опоры свободно, то одна опора считается шарнирно-неподвижной, другая – шарнирно-подвижной. Такая балка называется простой.
Деформации
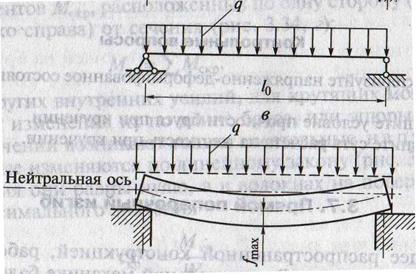
1. Если до загружения балка представляла собой прямолинейный стержень, то под нагрузкой стержень искривился и появился изгиб:
А) со стороны нагрузки стержень стал вогнутым (сжат);
Б) с противоположной стороны – выпуклым (растянут)
2. Деформации (неравномерное распределение)
А) при изгибе продольные волокна деформируются по-разному: одни удлиняются в нижней части балки, другие укорачиваются – в верхней части балки;
Б) эти удлинения и укорочения различны в зависимости от расположения волокон по отношению к середине сечения: чем ближе к краю, тем больше деформация.
В) нейтральная ось (слой) при искривлении свою длину не меняет. Нейтральная ось – разделяет участки сжатия и растяжения, меняет своё положение при увеличении нагрузки
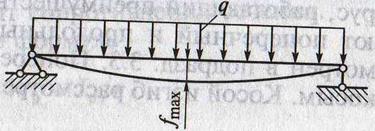
3. Прогиб – перемещения точек балки вниз вследствие искривления оси. Наибольший прогиб – в середине балки
fmax = 5384 ∙ ql4EJ
Внутренние усилия
1. В любом сечении по длине балки возникают:
А) изгибающие моменты Мх и
Б) поперечные силы Qx
2. Величина Мх и Qx зависит от:
А) расчётной схемы балки;
Б) характера нагрузки
3. Эпюры Мх и Qx для простой балки от равномерно распределённой нагрузки
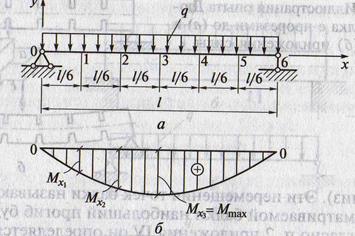

4. Наибольшее значение Мх определяют по формуле
Мхmax = ql28
5. Наибольшее значение Qх определяют по формуле
Qхmax = ql2
Напряжения
Нормальные напряжения
1. В соответствии с неравномерным распределением деформаций: напряжения по высоте сечения не одинаковы.
2. Наибольшее напряжение соответствует наибольшим деформациям (закон Гука)
3. Краевые части поперечного сечения, наиболее удалённые от середины по высоте сечения, находятся в напряжённом состоянии.
4. Следовательно, при определении напряжений при изгибе не обходимо учитывать не только количество материалов (Sсечения), но и его распределение по высоте сечения.
5. Наиболее выгодными при изгибе оказываются сечения, в которых основная масса материала расположена по краям элемента.
6. Распределение напряжений
А) в крайних верхних волокнах возникают наибольшие сжимающие напряжения σхсж. Условно принимают отрицательными → σхmin (верхние волокна укорачиваются)
Б) в крайних нижних — наибольшие растягивающие напряжения σхраст. Условно принимают положительными → σхmax (нижние волокна удлиняются)
В) на уровне нейтрального слоя (оси) σх = 0
7. Удлинения и укорочения зависят от расстояния до нейтрального слоя (оси)
8. Также от этого расстояния зависят и нормальные напряжения, т. е. они изменяются по линейному закону. График изменения нормальных напряжений σх (эпюра нормальных напряжений) — в
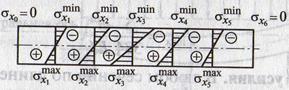
σхmax = σхmin = Mx : bh26 → σхmax = σхmin = MxWx
Момент сопротивления WX = bh26 – геометрический показатель сопротивления прямоугольного сечения изгибу (табличная величина)
(по аналогии аb — геометрический показатель сопротивления прямоугольного сечения растяжениюсжатию)
9. Из формулы – если размеры балки b и h одинаковы по длине балки, то нормальные напряжения
σх напрямую зависят от изгибающего момента Mx – чем больше изгибающий момент, тем больше нормальное напряжение.
10. В середине балки изгибающий момент достигает максимального значения и → напряжения (max и min) будут наибольшими для всей балки.
Касательные напряжения
1. Определяются по формуле Журавского
τу = QxSxJxb
Qx – поперечная сила в рассматриваемом сечении
Sx – статический момент сечения (по формулам или из таблиц)
Jx – момент инерции сечения
b – ширина сечения балки
Прим. Для описания явления изгиба используют такие характеристики, которые учитывают распределение материала по высоте сечения (эти характеристики называются геометрическими)
2. Из формулы – касательные напряжения зависят от поперечной силы Qx
А) там, где она достигает максимального значения (здесь: на опорах) наибольшими будут и касательные напряжения.
Б) где Qx = 0 (здесь: в середине балки) → τу =0
3. Касательные напряжения τу изменяются не по линейному закону (как σх), а по закону параболы
(τ зависит не только от Qx, но и от Sx – зависит от положения точки по высоте сечения)
4. График изменения напряжений по высоте сечения называется эпюрой (г — эпюра Q)
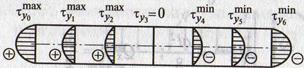
5. Для наглядности изменение касательных и нормальных напряжений показано в аксонометрии
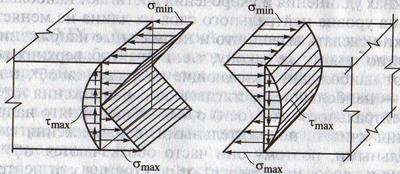
Примечания.
1. Нормальные напряжения направлены горизонтально (вдоль оси х) → индекс х
2. Касательные напряжения направлены вертикально (вдоль оси у) → индекс у
3. В обозначениях момента инерции J, момента сопротивления W, статического момента S — нижний индекс (Jх Wх Sх или у) – указывает на ось, относительно которой характеристики вычисляются.
Основные расчётные предпосылки при изгибе
1. Перпендикулярное оси недеформированного бруса плоское сечение остаётся и после изгиба плоским и нормальным к изогнутой оси бруса (гипотеза плоских сечений)
2. Продольные волокна при его деформации не надавливают друг на друга
Расчёт балок на прочность
1. По нормальным напряжениям
σизгmin, min ![]() Rизг
Rизг
Rизг – расчётное сопротивление материала при работе на изгиб (табличная величина)
Т. к.
σизг = МхWx → МхWx![]() Rизг
Rизг
2. Задачи трёх типов при расчётах на прочность при изгибе (как при растяжении и сжатии)
А) определение несущей способности балки
Б) проверка несущей способности балки
В) подбор сечения балки (встречается чаще)
2. По касательным напряжениям
τmax ![]() Rсдв
Rсдв
Rсдв – расчётное сопротивление материала при работе на сдвиг (табличная величина. Для стали вместо Rсдв → Rср)
QxSxJxb![]() Rсдв (срез)
Rсдв (срез)
Расчёт балок на жёсткость
(по деформациям)
1. Балки могут быть прочными и устойчивыми, но иметь чрезмерные (больше нормативных) прогибы
fmax ![]() fпред
fпред
fmax – наибольший расчётный прогиб конструкции
fпред – предельный прогиб по СНиП
2. Для междуэтажного перекрытия fпред = 1200 l, балок чердачного перекрытия fпред = 1150 l
где l – длина пролёта балки
Интеграл Мора и правило Верещагина
1. Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление.


