Нелинейные электродинамические процессы

На клеммах ячейки и ЭДС

индукции статора МГ-0

Скважность импульсов ;

: ;

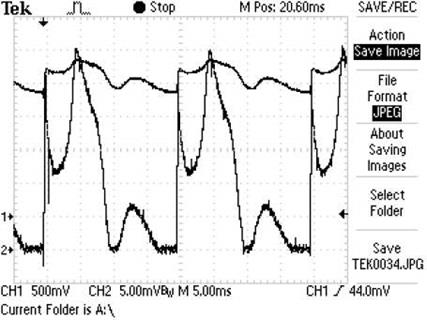
Рис. 65. Осциллограмма на клеммах ячейки, подключенной к генератору МГ-0

Видно (рис. 65), что мощность на клеммах ячейки нижнего генератора МГ — 0 равна 8,25 Вт. (рис. 62, а и b) меньше мощности на клеммах ячейки, подключённой к клеммам ЭДС самоиндукции статора МГ-1, которая равна 11,83Вт (рис. 64).

Импульсы ЭДС индукции на статоре МГ-1 не использовались. С учётом этого мощность, забираемая у первичного источника питания при нагрузке, равна 17,28Вт (рис. 63). Она меньше мощности, реализуемой электромотором на привод генератора (рис. 64) с близкой величиной полезной мощности в 181,70/17,28=10,50 раза. Кроме того, мощность, реализуемая первичным источником питания на привод ротора электромотора-генератора МГ-1 в 27,47/17,38=1,60 раза меньше механической мощности, генерируемой на валу ротора МГ-1. Суммарная электрическая мощность, генерируемая импульсами ЭДС самоиндукции статора МГ-1 и ЭДС индукции статора МГ-0, равна 11,83+8,25=20,08Вт. Она в 27,47/20,08=1,37 раза меньше механической мощности на валу ротора МГ-1. Это значит, что механическая мощность на валу ротора МГ-1 используется не полностью. Можно увеличивать длину магнитов или их количество.

Следующий эксперимент: подключение одной ячейки к клеммам ЭДС самоиндукции статора МГ-1 и ЭДС индукции статора МГ-0. Результаты эксперимента — на осциллограмме (рис. 66).

Рис. 66. Осциллограмма напряжения и тока на клеммах ячейки электролизёра, подключённой к клеммам ЭДС самоиндукции статора МГ-1 и ЭДС индукции статора МГ-0

Представленная и дополнительная экспериментальная информация, полученная при испытаниях МГ-2, использована при разработке технического задания на проектирование и изготовление МГ-3 (рис. 67). Начало испытаний МГ-3 намечено на май 2011г. Таким образом, новые законы новой электродинамики уже успешно реализуют свои возможности по экономии электрической энергии, производимой и потребляемой импульсами [4], [5], [6].

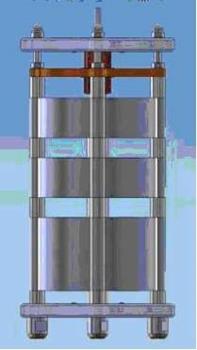
Рис. 67. Общий вид электромотора – генератора МГ-3

Итак, новые законы новой электродинамики уже выдают первые образцы экономных импульсных потребителей и импульсных генераторов электрической энергии.

20. Нелинейные электродинамические процессы

Наибольший интерес представляют нелинейные электродинамические процессы, из которых можно извлекать дополнительную энергию, используя эту нелинейность. Большая часть таких процессов связана с электричеством. Приборы же измеряющие электрическую энергию созданы только для линейных энергетических процессов, поэтому искажают учет её нелинейного расхода. Как обнаружить это искажение и устранить его?

Главная причина создавшегося положения заключается в том, что в основу устройства приборов, показывающих величины напряжения и тока положен линейный закон Ома, учитывающий линейно меняющееся сопротивление

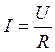. (49)

На заре рождения и использования электричества большая часть его потребителей имела линейно меняющиеся сопротивления . Тогда проблем точности учета электроэнергии не возникало. Они появились, когда началось освоение потребителей электрической энергии с нелинейно меняющимся сопротивлением и усилились при попытке использовать импульсные потребители электроэнергии. Наиболее ярким нелинейным энергетическим процессом является плазмоэлектролитический процесс. Он возникает при электролизе воды в условиях, когда площадь катода в десятки раз меньше площади анода (рис. 68, a, b).

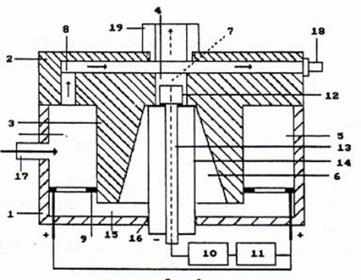
Рис. 68. а) модель плазмоэлектролитической ячейки;

b) плазмоэлектролитическая ячейка в действии

Главной характеристикой плазмоэлектролитического процесса является его вольтамперная характеристика, в которой отражена зависимость изменения тока от напряжения, то есть – фактически закон Ома.

На рис. 69 представлена вольтамперная характеристика плазмоэлектролитической ячейки, работавшей с одномолярным раствором соляной кислоты HCl. Как видно (рис. 69), при повышении напряжения до 40В линейно, в соответствии с законом Ома (6), растет сила тока (рис. 69). Затем, при напряжении более 40В линейность изменения тока нарушается, а при напряжении около 100 Вольт (точки 5 — 6) сила тока уменьшается скачкообразно и у катода появляется яркое свечение (рис. 68, b) — плазма. Дальнейшее принудительное уменьшение напряжения (точки 7 — 8) незначительно изменяет силу тока. При напряжении около 60 Вольт (точки 8 — 9) свечение у катода исчезает, сила тока скачкообразно увеличивается почти до прежней величины [1].

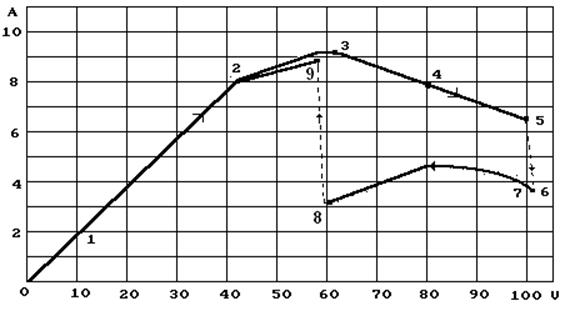
Рис. 69. Вольтамперная характеристика плазмоэлектролитической ячейки

Вольтамперная характеристика индивидуальна для каждой ячейки и режима её работы. Она зависит от конструктивных параметров ячейки, используемых материалов катода и анода, концентрации и химического состава раствора, а также от его расхода (рис. 70).

Влияние расхода раствора KOH на вольтамперную характеристику представлено на рис. 70. Во всех трех группах экспериментов устойчивая плазма у катода появляется при напряжении около 100 Вольт и исчезает при понижении напряжения до 85 Вольт. В период существования плазмы наблюдался интенсивный выход парогазовой смеси.

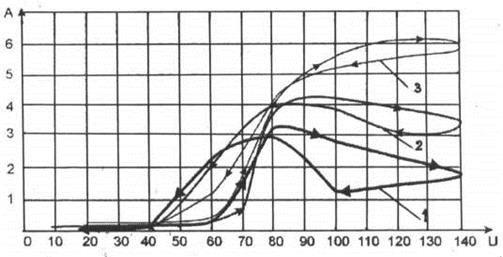
Рис. 70. Вольтамперные характеристики плазмоэлектролитического процесса при расходе раствора КОН: 1 – 3,6 л/ч; 2 – 8,2 л/ч; 3 – 12,2 л/ч

Зависимость между изменением тока и напряжения (рис. 69) линейна в интервале изменения напряжения от нуля до 43В, примерно. В этом диапазоне чётко работает закон Ома (49) и чётко определяется величина средней мощности, реализуемой на этот процесс. При большем напряжении линейная зависимость между напряжением и током исчезает и нарушается работа линейного закона Ома (49). Нелинейную зависимость между напряжением и током невозможно описать классическим законом Ома (49). А как же тогда учитывать электрическую энергию, потребляемую в этом случае, если приборы для измерения напряжения и тока базируются на линейном изменении напряжения и тока, следующего из линейного закона Ома? Можно ли доверять в таких случаях показаниям приборов?

Специалисты давно заметили, что на отдельных участках электрической цепи теряется линейная зависимость между током и напряжением, и начали вводить математические модели для описания нелинейных процессов. Но их разнообразие оказалось настолько большим, что исключается возможность получения единой математической модели для их описания. Как мы уже отметили, за решение столь сложной проблемы взялись математики. Учитывая важность понимания процесса формирования их ошибки, повторим его описание. Они выразили закономерность изменения напряжения в виде функции , а закономерность изменения тока в виде функции . В результате формула для расчёта средней величины мощности приняла вид (32).