Планы скоростей механизмов
Для определения указанных неизвестных величин строим план скоростей в выбранном масштабе скорости mv. Из произвольного полюса pv (рис.4,б) проводим вектор рvа =VA/mv, перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости VA. Из конца вектора рvа (точка а) проводим линию в направлении относительной скорости , перпендикулярную АВ, а из полюса pv – линию в направлении скорости VB, параллельную ОВ В пересечении указанных линий находим точку b. Вектор рvb изображает скорость точки В, а вектор ab – скорость ![]() . Значения действительных скоростей находим по формулам:
. Значения действительных скоростей находим по формулам:
VB = mv∙ рvb и
VBA = mv∙ ab
Для определения скорости точки С шатуна можно воспользоваться известной из теоретической механики теоремой подобия для скоростей, согласно которой отрезки прямых линий, соединяющие точки на схеме звена механизма и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90° (свойство планов скоростей).
Вектор рvс скорости точки С находим построением на отрезке ab треугольника abc , подобного треугольнику ABC, повернутому на 90°. Для этого из точки а плана скоростей проводим линию, перпендикулярную АС, а через точку b – перпендикулярную ВС. Значение скорости в этой точке вычисляем по формуле
VC= mv∙рvс
Угловая скорость звена 2
w2 = VBA/lBA
Направление w2 находится по вектору скорости VBA.
Планы скоростей механизмов позволяют охарактеризовать движение механизма:
– векторы, выходящие из полюса плана скоростей (рv) , представляют собой абсолютные скорости;
– вектор, соединяющий концы абсолютных скоростей, представляют собой относительную скорость; он направлен к той точке, которая стоит первой в индексе скорости;
– план скоростей дает возможность находить касательные к траекториям точек механизма, не выстраивая этих траекторий;
– полюс плана скоростей (рv) соответствует мгновенному центру вращения звена (МЦВ).
Построение плана ускорений начинают с построения абсолютного ускорения aA точки А кривошипа, складывающегося геометрически из суммы нормальной (aAn = w12∙lOA) тангенциальной (aAt = e1∙lOA) составляющих:
aA = aAn + aAt 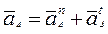 .
.
При 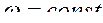
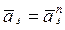 =
=![]()
![]() Выбрав масштаб плана ускорений ma, из произвольной точки pa (рис.4в), называемой полюсом плана ускорений, откладываем ускорение aAn в виде вектора paа, направленного от точки А к точке О (рис.4а)
Выбрав масштаб плана ускорений ma, из произвольной точки pa (рис.4в), называемой полюсом плана ускорений, откладываем ускорение aAn в виде вектора paа, направленного от точки А к точке О (рис.4а)
Ускорение точки В находим из уравнения
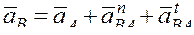
Значение нормальной составляющей относительного ускорения определяется по формуле
= w22∙lAВ
Вектор ![]() направлен по АВ к центру вращения (к точке А механизма) и откладывается из точки а плана. В виде отрезка an =
направлен по АВ к центру вращения (к точке А механизма) и откладывается из точки а плана. В виде отрезка an = ![]() /ma. Направление тангенциальной составляющей вектора
/ma. Направление тангенциальной составляющей вектора ![]() будет проходить через конец n вектора
будет проходить через конец n вектора ![]() и перпендикулярно к нему. Направление абсолютного ускорения точки В известно (аВ // ОВ) и соответствующая линия проходит через полюс ра.. Пересечение этих двух линий определит положение точки b на плане ускорений, а следовательно, величину ускорения аВ = ma∙раb. Вектор ab изображает полное ускорение
и перпендикулярно к нему. Направление абсолютного ускорения точки В известно (аВ // ОВ) и соответствующая линия проходит через полюс ра.. Пересечение этих двух линий определит положение точки b на плане ускорений, а следовательно, величину ускорения аВ = ma∙раb. Вектор ab изображает полное ускорение ![]() . Угловое ускорение звена 2 находим по формуле
. Угловое ускорение звена 2 находим по формуле
e2∙= atВА/lAВ.
Перенося вектор ускорения ![]() в точку В и рассматривая движение точки В относительно точки А, находим направление e2.
в точку В и рассматривая движение точки В относительно точки А, находим направление e2.
Вектор рас ускорения точки С находим, используя свойство плана ускорений, построением на отрезке ab треугольника abc, подобного треугольнику АВС, повернутого на угол (180° — a), где
a = arctge2/w22
Значение ускорения в этой точке равно аC = ma∙раc.
План ускорений имеет следующие характеристики:
· векторы, выходящие из полюса ра плана ускорений, представляют собой абсолютные ускорения соответствующих точек звеньев механизма;
· отрезки, расположенные между концами векторов абсолютных ускорений, соответствуют полным относительным ускорениям;
· концы векторов абсолютных ускорений точек, принадлежащих одному звену механизма, на плане ускорений образуют подобные фигуры, повернутые на угол (180° — a);
· план ускорений позволяет находить угловые ускорения звеньев.
Вопросы для самопроверки:
1. Сформулируйте задачи и назовите методы кинематического анализа рычажных механизмов?
2.Как строятся крайние положения и траектории точек звеньев механизма?
3.Постройте план скоростей и ускорений кривошипно-коромыслового и кривошипно-ползунного механизмов.
4.Запишите формулу ля вычисления угловых скоростей и ускорений. Определите их направление.
5 Как следует определять скорость (ускорение) третьей точки звена при известных векторах скоростей (ускорений) двух точек звена, используя свойство
3.СИЛОВОЙ АНАЛИЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ
3.1. Силы, действующие в машинах
Развитое машинное устройство, состоящее из двигателя, передаточных механизмов и рабочей машины и, в некоторых случаях, контрольно-управляющих машин, называется машинным агрегатом. К механизмам машинного агрегата во время его движения приложены различные силы. В зависимости от знака элементарной работы все эти силы подразделяются на силы движущие Fд (М д ) и силы сопротивленияF с (Mс), силы тяжести G и инерционные силы Fи (Mи), силы взаимодействия между k-тым и i-тым звеньями механизмов т. е. силы, действующие в кинематических парах (реакции в кинематических парах Rki). Движущей силой называется сила, элементарная работа которой положительна, а силой сопротивления — сила элементарная работа которой отрицательна. Элементарная работа силы определяется как скалярное произведение силы на элементарное перемещения точки ее приложения. Силы сопротивления в свою очередь делятся на силы Fпс (или моменты сил Mпс) полезного сопротивления (силы, для преодоления которых предназначена данная машина) и силы Fвс (или моменты сил Mвс) вредного сопротивления(силы трения и силы сопротивления окружающей среды). Для определения силы трения рекомендуется использовать формулу Амонтона-Кулона. Силы тяжести G могут быть или силами движущими, или силами сопротивления в зависимости от направления перемещения центра тяжести звена.
Инерционные силы Fи и их моменты Mи определяются по известным из теоретической механике формулам: ![]()


