Неоднородное уравнение даламбера
где 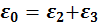 — результирующая напряженность.
— результирующая напряженность.
![]()
где 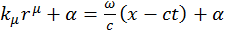 .
.
Для анализа поляризации зафиксируем координату x так, чтобы 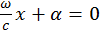 . Тогда в этой точке x останутся чисто гармонические колебания (во взаимно ортогональных направлениях: y и z), и вектор напряженности будет иметь вид:
. Тогда в этой точке x останутся чисто гармонические колебания (во взаимно ортогональных направлениях: y и z), и вектор напряженности будет иметь вид:
![]()
Выделим действительную часть вектора напряженности электрического поля ![]() .
.
![]()
В нашем разложении оба вектора изменяются по одинаковому закону:
![]()

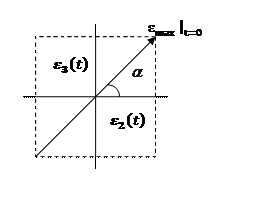 Т. о. наши колебания вектора напряженности электрического поля происходят следующим образом:
Т. о. наши колебания вектора напряженности электрического поля происходят следующим образом: ![]() достигает максимального значения в том случае, если t=0. С включением времени,
достигает максимального значения в том случае, если t=0. С включением времени, ![]() убывает, так как косинус убывает, но время идет, и следовательно,
убывает, так как косинус убывает, но время идет, и следовательно, ![]() пойдет в отрицательную сторону.
пойдет в отрицательную сторону.
Таким образом, у нас вектор напряженности электрического поля колеблется вдоль одной прямой. Т. о. мы имеем дело с линейной поляризацией.
г) Эллиптическая поляризация плоской монохроматической волны.
Рассмотрим случай, когда фазовые множители связаны соотношением:
![]()
где 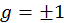 . Тогда амплитуда колебаний имеет вид:
. Тогда амплитуда колебаний имеет вид:
![]()
Зная, что 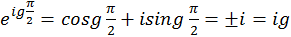 , получаем:
, получаем:
![]()
Выделим действительную часть комплексной амплитуды:
![]()
![]()
Можно найти траекторию кончика результирующего вектора ![]() .
.
![]()

Следовательно, конец вектора ![]() будет двигаться по траектории эллипса.
будет двигаться по траектории эллипса.
Получили эллиптические колебания, следовательно, имеем эллиптическую поляризацию.
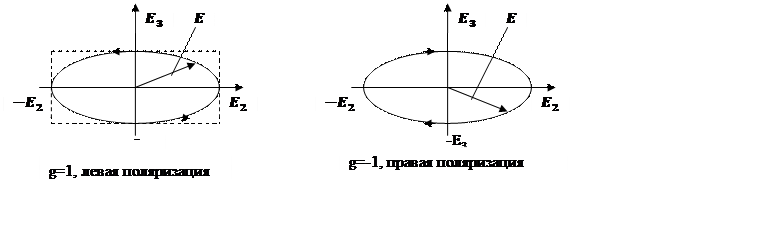
Если 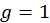 – правая эллиптическая поляризация (см. рис.). В случае, когда
– правая эллиптическая поляризация (см. рис.). В случае, когда 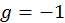 – левая. Если
– левая. Если 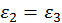 , то эллиптическая поляризация переходит в круговую, если
, то эллиптическая поляризация переходит в круговую, если ![]() или
или ![]() равен нулю – вырождается в линейную.
равен нулю – вырождается в линейную.
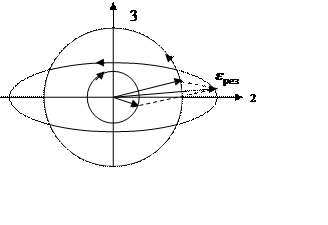
Оказывается, что эллиптическую поляризацию всегда можно представить в виде суммы двух круговых поляризаций. Причем степень эллиптичности зависит от того, какой будет разница между амплитудами. Это продемонстрировано на рисунке ниже.
§ 5.4. Неоднородное уравнение Даламбера.
Запаздывающие и опережающие потенциалы
В данном параграфе мы получим неоднородное волновое уравнение при наличии токов и зарядов, которые создают поля. Для этого рассмотрим уравнение потенциалов при наличии токов, его можно получить исходя из второй пары уравнений Максвелла:
![]()
Раскроем тензор электромагнитного поля:
![]()
Пользуясь неоднородностью потенциалов, наложим на них дополнительное условие –калибровка Лоренца:
![]()
Используя этот (5.4.2) для (5.4.1) получим:
![]()
![]()
Выражение (5.4.4) – неоднородное уравнение Даламбера.
Подставляя μ=0,1,2,3,, запишем:

Найдем решение этих уравнений.
|
|
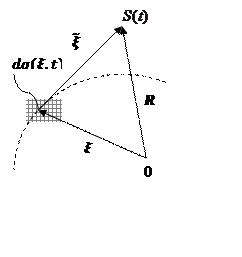
Эти уравнения (5.4.5) с математической точки зрения одинаковы. Решим уравнение для скалярного потенциала. Для определенности будем рассматривать случай точечного заряда. Поступим следующим образом, разобьем заряд на маленькие заряды. Т. к. мы работаем в теории поля (рис. 5.4.1), нельзя использовать понятия траектории и точечного заряда. Плотность заряда задается следующим образом: Тогда наше уравнение (5.4.5) перепишется в виде: |
![]()
Решение находим в два этапа.
1. Решим уравнение вне клеточки, где находится заряд. Будем считать, что точка S находиться на очень большом расстоянии. В этом случае правая часть уравнения равна нулю.
![]()
Т. к. размеры заряда ничтожно малы, следовательно, можно считать, что наш потенциал будет обладать сферической симметрией, запишем лапласиан в сферической системе координат.