Общий порядок расчёта балки

2. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр (метод перемножения эпюр).

Общий порядок расчёта балки

для задач типа III

1. Построение эпюр Мх и Qх

2. Подбор сечения балки (размеров)

А) определение требуемого момента сопротивления балки

Wxтреб Мmax Rизг

Б) по значению Wx подбирают номер балки (и её размер)

3. Проверка прочности подобранной балки по нормальным напряжениям

МmaxWx Rизг

Wx – момент сопротивления выбранного сечения

4. Построение эпюры нормальных напряжений

5. Проверка прочности подобранной балки по касательным напряжениям по формуле Журавского

τу = QxSxJxb

Qx – поперечная сила в рассматриваемом сечении

Sx – статический момент сечения (по формулам или из таблиц)

Jx – момент инерции сечения

b – ширина сечения балки

6. Построение эпюры касательных напряжений

7. Проверка жёсткости балки

Понятие о рациональных формах простых балок

1. Рациональные конструкции – наиболее экономичные.

2. Наиболее обобщённый показатель экономичности – собственный вес балки – чем меньше вес, тем она рациональнее (экономичнее)

3. Вес балки напрямую связан с размерами – чем меньше размеры балки и её сечения, тем она экономичнее (при соблюдении прочности)

Самостоятельная работа обучающихся (эзс – 6 час, арх – 6 час, авто – 5)

1. Построить эпюры поперечных сил и изгибающих моментов по длине балки по вариантам

2. Рассчитать балки на прочность по нормальным, касательным и эквивалентным напряжениям по вариантам

3. Составить краткий алгоритм решения задач на определение линейных и угловых перемещений при поперечном изгибе статически определимых балок

1. Расчётно­-графическая работа на построение эпюр попереч­ных сил, изгибающих моментов и расчёт на прочность при изгибе — авто

ТЕМА 2.6. КРУЧЕНИЕ(4.6. – АВТО)

(эзс – 2 час, арх – 1 час, авто – 2)

Кручение прямого бруса круглого сечения.

1. Кручение – вид нагружения, при котором в поперечных сечениях возникает только крутящий момент.

2. Прочие внутренние силовые факторы (нормальная и поперечная силы, изгибающие моменты) равны нулю.

3. Пример: круглый брус, жёстко заделанный в стену. На свободном торце приложен скручивающий момент М.

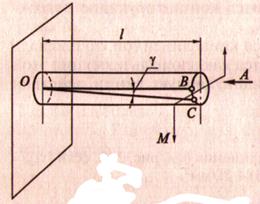
Деформации

От скручивающего момента брус деформируется:

1. Смежные сечения поворачиваются относительно друг друга

2. Образующая ОВ искривляется и занимает положение АС

Допущения при рассмотрении кручения

1. Ось бруса не деформируется

2. Плоские до деформации поперечные сечения остаются плоскими и после деформации

3. Продольные волокна не изменяют своей длины (угол γ настолько мал, что изменением длины можно пренебречь)

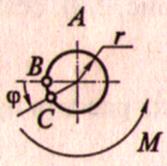
Правило знаков для крутящих моментов

1. Если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит внутренний крутящий момент Мкр против часовой стрелки, то момент считается положительным.

2. По часовой стрелке — отрицательным.

Напряжения в поперечном сечении бруса при кручении.

А) При кручении в поперечном сечении бруса возникают касательные напряжения (чистый сдвиг)

Б) касательные напряжения τ при кручении распределяются в сечении по линейной зависимости: в центре равны нулю, на максимальном радиусе – максимальное значение τmax (по которому ведётся расчёт)

В) Значение τmax зависит от внутреннего крутящего момента и геометрической характеристики поперечного сечения

τmax = МкрWр

Wр – полярный момент сопротивления

Wр = 0,2 D3 – для сплошного сечения

Wр = 0,2 D3 (1 – d4D4)

d – внутренний диаметр (диаметр отверстия)

D – внешний диаметр бруса (авто – вала)

Понятие угла закручивания

А) существуют понятия угла закручивания φ и относительного угла закручивания θ

Б) зависимость между φ и θ

θ = φl

φ = МкрlGWpr

Wpr = Jp – полярный момент инерции сечения

Jp = 0,1D4 – для сплошного круглого бруса

Jp = 0,1D4 (1 – d4D4) – для полого круглого бруса

G Jp – жёсткость поперечного бруса при кручении

Построение эпюр крутящих моментов, касательных напряжений и углов закручивания

1. При кручении, как и при растяжении, строят:

А) эпюры внутренних силовых факторов – крутящих моментов (при растяжении – нормальных сил);

Б) эпюры касательных напряжений τ (при растяжении – нормальных σ)

В) эпюры углов закручивания φ (при растяжении – перемещений)

2. Рисунок стр.78

— разделим брус на 3 части – до силы М2, от силы М2 до силы М1, после силы М1

3. Условное обозначение:

А) кружок с точкой – сила, направленная на наблюдателя;

Б) кружок с крестиком — сила, направленная от наблюдателя.

Построение эпюры Мкр

1. Участок III не загружен – момент на эпюре равен нулю.

2. М1 – сила направлена против часовой стрелки: знак +

На эпюре от силы М2 до силы М1 –на участке II значение 2М

Контроль: на эпюре скачок 2М

3. В точке воздействия М2: +М1 – М2 = 2М-М = М

– на участке I значение М

Контроль: на эпюре скачок М

Построение эпюры τ max

τmax = МкрWр

1. Участок I

Мкр = +М (с эпюры Мкр → Wp = 0,2• (2d)3 = 1,6 d3 τ max= М/1,6 d3

2. Участок II

Мкр = +М Wp = 0,2d3 → Wp = 0,2• (d)3 = 0,2 d3 τ max= М/0,2d3•55 = 5М d3

3. Участок III

Мкр = +2М Wp = 0,2d3 τ max= 2М/0,2 d3•55 = 10М d3

4. Участок IV

Мкр = 0 Wp = 0,2d3 τ max= 0,2d3 = 0

Wp – полярный момент сопротивления (геометрический фактор, на который воздействует изгибающий момент)

Для сплошного сечения Wp = 0,2D3

Так как все внутренние крутящие моменты имели положительный знак, то и касательные напряжения τ max будут положительны.

Построение эпюры φ (углов закручивания)

1. Участок I

φ= МкрIl : GJpI = М • l G • 0,1(2d)4 = Мl G • 0,1•2•2•2•2•d4 = М • l G •1,6•d4

2. Участок II

φ = МкрII l : GJpII

Под общий знаменатель принимаем G •d4

(1 : 1,6 = 0,6 1 : 0,1 = 10)

3. Участок III

φ = МкрIII • l : GJpIII

3. Участок IV

30,6М • l G •d4 + 0• lG •d4 = 30,6М • l G •d4 (постоянная величина на этом участке)