Олимпиада по физике с решениями
8 класс
1. При помощи подвижного блока груз массой 20 кг был поднят на высоту 5 м. Определите КПД механизма, если к концу троса было приложено усилие 200 Н.
Решение
Для определения КПД необходимо найти полезную и совершенную работы. Полезная работа, необходимая для подъема груза, равна 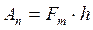 , где
, где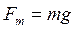 . Тогда
. Тогда 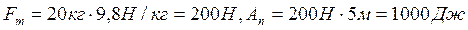 . Совершенная работа определяется по формуле
. Совершенная работа определяется по формуле 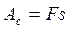 , где s – перемещение веревки. Так как используется подвижный блок, то согласно «золотому правилу механики»
, где s – перемещение веревки. Так как используется подвижный блок, то согласно «золотому правилу механики» 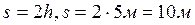 . Тогда
. Тогда 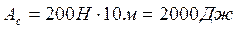 . КПД найдем по формуле
. КПД найдем по формуле 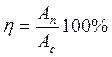 . Рассчитаем:
. Рассчитаем: 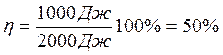
Критерий оценивания (по 1 баллу)
1) Определение силы тяжести груза.
2) Определение полезной работы, необходимой для подъема груза.
3) Определение перемещения веревки.
4) Определение совершенной работы.
5) Записана формула для КПД.
6) Расчет КПД.
2. Дайте физическое обоснование пословице: «Коси коса пока роса, роса долой и мы домой».
Решение
Роса увеличивает массу стебля. Поэтому при ударе косой он в меньшей степени изгибается, и коса сразу срезает его.
Роса создает смазку и уменьшает силу трения, когда при обратном движении косы она скользит по траве.
Критерий оценивания (по 1 баллу)
1) Установлена зависимость изменения скорости частей стебля от их массы.
2) Установлена зависимость деформации стебля от изменения скорости его частей.
3) Установлена зависимость результата действия силы от деформации стебля.
4) Установлена зависимость силы трения от смазки.
5) Установлено возникновение трения при обратном движении косы.
6) Установлено скольжение косы по траве.
3. Во льдах Арктики в центре небольшой плоской льдины стоит белый медведь массой m = 700 кг. Какой массы должна быть льдина, чтобы медведь не замочил своих лап?
Решение
Чтобы медведь не замочил лап, льдина должна быть на плаву, погрузившись полностью в воду. При этом сила тяжести, действующая на льдину с медведем, равна выталкивающей силе, действующей на льдину, т. е. FT1+FT2=FA, где ![]() . Объем льдины V можно определить по формуле
. Объем льдины V можно определить по формуле 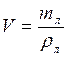 .где mл и ρл – масса и плотность льдины. Сила тяжести, действующая на льдину с медведем равна
.где mл и ρл – масса и плотность льдины. Сила тяжести, действующая на льдину с медведем равна 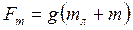 . Применяя условие плавания тела, получим:
. Применяя условие плавания тела, получим: 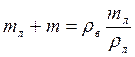 . После алгебраических преобразований найдем массу льдины:
. После алгебраических преобразований найдем массу льдины: 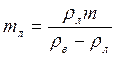 . Расчеты дают:
. Расчеты дают: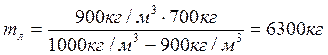 .
.
Критерий оценивания (по 1 баллу)
1) Записано условие плавания тел.
2) Записана формула для определения силы Архимеда.
3) Определен объем круга.
4) Записана формула для определения общей силы тяжести, действующей на круг с человеком.
5) Получена расчетная формула для определения массы круга.
6) Произведен расчет массы круга.
4. Школьники побывали в музее-имении Л. Н. Толстого «Ясная поляна» и возвращались в Рязань на автобусах, которые ехали со скоростью v1 = 70 км/ч. Пошел дождь, и водители снизили скорость до v2 = 60 км/ч. Когда дождь кончился, до Рязани оставалось проехать S = 40 км. Автобусы поехали со скоростью v3 = 75 км/ч и въехали в Рязань в точно запланированное время. Сколько времени шел дождь? Чему равна средняя скорость автобуса? Для упрощения считайте, что автобусы в пути не останавливались.
Решение
Средняя скорость автобуса – это отношение пройденного пути к затраченному времени. Так как расстояние от «Ясной поляны» до Рязани из-за дождя не изменилось, и время, проведенное школьниками в автобусе, также не изменилось (потому что автобусы въехали в Рязань в точно запланированное время), то средняя скорость совпадает с начальной скоростью vср = 70 км/ч.
Пусть дождь шел в течение времени t. Тогда путь, пройденный за это время, составил v2·t. Время, за которое после дождя автобусы проехали оставшееся расстояние, равно S/v3. Ясно, что время, затраченное автобусами с момента начала дождя до прибытия в Рязань, должно равняться времени, которое потребовалось бы для преодоления того же расстояния с начальной скоростью v1:
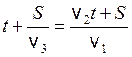 .
.
Отсюда находим время, в течение которого шел дождь:
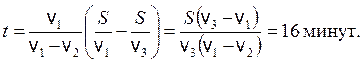
Критерий оценивания (по 1 баллу)
1) Определена средняя скорость.
2) Выражено время прохождения отдельных участков пути.
3) Установлено равенство времени движения с момента начала дождя до прибытия в Рязань и времени, которое потребовалось бы для преодоления того же расстояния с начальной скоростью v1. (2 балла).
4) Получена формула для расчета времени, в течение которого шел дождь.
5) Расчет времени, в течение которого шел дождь.
9 класс
1.Найдите отношение масс спирта и бензина в смеси, удельная теплота сгорания которой q0=41 МДж/кг. Удельная теплота сгорания бензина, q1=44 МДж/кг, а удельная теплота сгорания спирта q2=26 МДж/кг.
Решение
Количество теплоты, выделяемое при сгорании смеси равно количеству теплоты, выделяемому при сгорании спирта и бензина, содержащихся в смеси, т. е. Q0=Q1+Q2. Смесь, сгорая, выделяет ![]() , бензин —
, бензин — 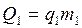 , спирт
, спирт 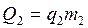 . Тогда
. Тогда 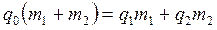 . Разделим обе части уравнения на m1 и получим
. Разделим обе части уравнения на m1 и получим 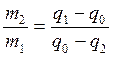 . Расчет дают
. Расчет дают 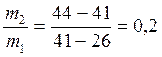 .
.
Критерий оценивания (по 1 баллу)
1. Установлена связь между количествами теплоты, выделяемыми смесью, и компонентами её частей.
2. Определена масса смеси как сумма масс её компонентов.
3. Записаны формулы для количеств теплоты, выделенных при сгорании топлива.
4. Выражена масса спирта или разделено уравнение на массу бензина.
5. Получена формула отношения масс.
6. Произведен расчет.
2.Сварочный аппарат присоединяют в сеть напряжением 380В медными проводами длиной 100 м и площадью поперечного сечения 50 мм2. Определите мощность сварочного аппарата, если сила тока в нем 125 А.
Удельное сопротивление меди равно 0,017 Ом мм2/м.
Решение.
Сопротивление проводов определяется по формуле 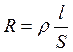 . Напряжение на проводах равно Uп=IR. Тогда напряжение на сварочном аппарате Uc= U-Uп, и его мощность P=IUс, или
. Напряжение на проводах равно Uп=IR. Тогда напряжение на сварочном аппарате Uc= U-Uп, и его мощность P=IUс, или 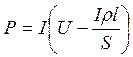
Произведенный расчет дает значение 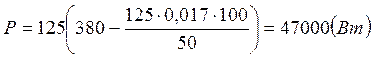
Критерии оценивания (по 1 баллу)
1. Определено сопротивление проводов
2. Определено напряжение на проводах
3. Определено напряжение на сварочном аппарате
4. Определена мощность сварочного аппарата
5. Получена расчетная формула
6. Произведен расчет по формуле или по действиям.
3.Во льдах Арктики в центре небольшой плоской льдины площадью S = 70 м2 стоит белый медведь массой m = 700 кг. При этом надводная часть льдины выступает над поверхностью воды на высоту h = 10 см. На какой глубине под водой находится нижняя поверхность льдины? Плотность воды rв = 1000 кг/м3, плотность льда rл = 900 кг/м3.
Решение
Обозначим через x искомую глубину. Тогда масса льдины равна m=ρЛ∙V, где V=S(h+x). Сила тяжести, действующая на льдину с медведем, равна:
Fт =g[m + rлS(h + x)]. Она должна равняться силе давления воды на нижнюю поверхность льдины, находящуюся на глубине x (силе Архимеда): FА =rвgVп, где Vп=xS, поскольку льдина находится в состоянии равновесия. Отсюда получаем: 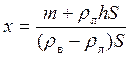 . Произведенный расчет дает значение
. Произведенный расчет дает значение 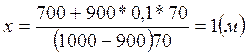 .
.
Критерии оценивания (по 1 баллу)
1. Определена масса льдины
2. Определена общая сила тяжести
3. Определена сила Архимеда
4. Применено условие плавания тел
5. Получена расчетная формула
6. Произведен расчет по формуле.
4. В калориметр с водой при температуре 20°С опустили тело массой 152 г при температуре 100°С. Температура поднялась до 30°С. Не вынимая тело, в сосуд налили 100 г воды при 100°С, при этом температура поднялась до 60°С. Определите удельную теплоемкость тела. Теплоемкостью калориметра не пренебрегать. Удельная теплоемкость воды 4200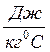 .
.
Решение
Калориметр с водой получают количество теплоты, равное 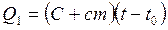 , где С – теплоемкость калориметра, c, m – удельная теплоемкость и масса воды, находящейся в калориметре. Тело, опущенное в воду, отдает количество теплоты, равное
, где С – теплоемкость калориметра, c, m – удельная теплоемкость и масса воды, находящейся в калориметре. Тело, опущенное в воду, отдает количество теплоты, равное 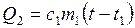 , где c1, m1, t1 — удельная теплоемкость, масса и начальная температура тела. Запишем уравнение теплового баланса для первого процесса Q1+Q2=0, т. е.
, где c1, m1, t1 — удельная теплоемкость, масса и начальная температура тела. Запишем уравнение теплового баланса для первого процесса Q1+Q2=0, т. е.
(C+cm)(t-t0) = c1 m1 (t-t1). Отсюда можно выразить C+cm=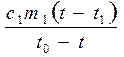 (1).
(1).
После доливания горячей воды, которая отдаст количество теплоты, равное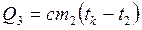 , где m2, t2 — масса и начальная температура горячей воды, а tk – конечная температура, содержимое калориметра получит количество теплоты, равное
, где m2, t2 — масса и начальная температура горячей воды, а tk – конечная температура, содержимое калориметра получит количество теплоты, равное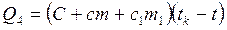 . Запишем уравнение теплового баланса для второго процесса Q3+Q4=0, т. е.
. Запишем уравнение теплового баланса для второго процесса Q3+Q4=0, т. е. 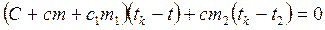 (2).
(2).
Подставив первое выражение во второе, получим расчетную формулу:
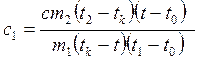 . При расчете получим:
. При расчете получим: 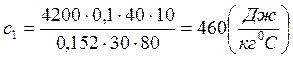
Критерии оценивания (по 1 баллу).
1. Записаны уравнения количеств теплоты, которые получат калориметр с водой, и отдаст тело, опущенное в воду.
2. Записано уравнение количества теплоты, которое отдаст после доливания горячая вода.
3. Записано уравнение количества теплоты, которое получит после доливания горячей воды содержимое калориметра.
4. Записано уравнение теплового баланса для первого и второго процессов.
5. Получена расчетная формула.
6. Произведен расчет по формуле.
10 класс
1. Мотоциклист, начав движение из состояния покоя, едет с постоянным ускорением 0,8 м/с2. Какой путь он пройдет за десятую секунду своего движения.
Решение
I способ
За десятую секунду мотоциклист прошел путь, равный разности путей, пройденных за десять и девять секунд, т. е. S =S10 – S9. Поскольку V0 = 0, 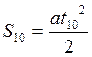 ;
; 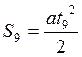 , где t10 = 10 c, а t9 = 9 с. Тогда
, где t10 = 10 c, а t9 = 9 с. Тогда 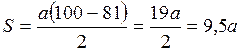 При расчете получим: S = 9,5∙0,8 = 7,6 (м).
При расчете получим: S = 9,5∙0,8 = 7,6 (м).
II способ
Путь, пройденный мотоциклистом за десятую секунду, можно определить так: S = Vср∙t, где t=1 с, а Vср = 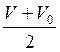 , так как движение равноускореное.
, так как движение равноускореное.
V = at10 – скорость, приобретенная к концу десятой секунды,
V0 = at9 — скорость, приобретенная к концу девятой секунды, поскольку V0=0. Тогда 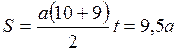 . При расчете получим: S = 9,5∙0,8 = 7,6 (м).
. При расчете получим: S = 9,5∙0,8 = 7,6 (м).
Критерии оценивания (по 1 баллу).
I способ
1. Выражение пути, пройденного мотоциклистом за 10-ю секунду через пути, пройденные за десять и девять секунд. (2 балла)
2. Определение пути, пройденного за 10 с.
3. Определение пути, пройденного за 9 с.
4. Получение расчетной формулы.
5. Произведен расчет по формуле или по действиям.
II способ (по 1 баллу)
1. Выражение пути, пройденном мотоциклистом за 10-ю секунду через среднюю скорость.
2. Определение средней скорости равноускоренного движения.
3. Определение начальной скорости на последней секунде.
4. Определение конечной скорости на последней секунде.
5. Получена расчетная формула
6. Произведен расчет по формуле или по действиям.
2. Найдите отношение масс спирта и бензина в смеси, удельная теплота сгорания которой q0=41 МДж/кг. Удельная теплота сгорания бензина, q1=44 МДж/кг, а удельная теплота сгорания спирта q2=26 МДж/кг.
Решение
Количество теплоты, выделяемое при сгорании смеси равно количеству теплоты, выделяемому при сгорании спирта и бензина, содержащихся в смеси, т. е. Q0=Q1+Q2. Смесь, сгорая, выделяет ![]() , бензин —
, бензин — 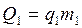 , спирт
, спирт 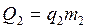 . Тогда
. Тогда 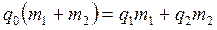 . Разделим обе части уравнения на m1 и получим
. Разделим обе части уравнения на m1 и получим 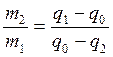 . Расчет дают
. Расчет дают 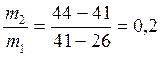 .
.
Критерий оценивания
1. Установлена связь между количествами теплоты, выделяемыми смесью, и компонентами её частей.
2. Определена масса смеси как сумма масс её компонентов.
3. Записаны формулы для количеств теплоты, выделенных при сгорании топлива.
4. Выражена масса спирта или разделено уравнение на массу бензина.
5. Получена формула отношения масс.
6. Произведен расчет.
3. Моток проволоки имеет сопротивление 1000 Ом. Максимальный ток, который выдерживает данная проволока, равен 1А. Какой максимальной тепловой мощности нагреватель можно изготовить из данной проволоки, если он будет включаться в розетку с напряжение 220В.
Решение
Максимальная тепловая мощность нагревателя опреднляется по формуле: 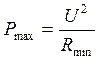 , Минимальное сопротивление нагреватель будет иметь, если проводники, из которых он состоит соединить параллельно, т. е.
, Минимальное сопротивление нагреватель будет иметь, если проводники, из которых он состоит соединить параллельно, т. е. 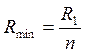 , где R1 – сопротивление каждого из n кусков проволоки, которые соединены параллельно. Если моток разрезали на n частей, то сопротивление одной проволоки равно
, где R1 – сопротивление каждого из n кусков проволоки, которые соединены параллельно. Если моток разрезали на n частей, то сопротивление одной проволоки равно 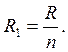 Тогда
Тогда 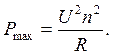 Т. к. извесен максимальный ток, который выдерживает данная проволока, то сила тока в нагревателе будет равна
Т. к. извесен максимальный ток, который выдерживает данная проволока, то сила тока в нагревателе будет равна 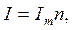 и
и 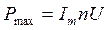 , тогда
, тогда 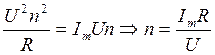 .
.
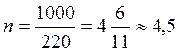 т. е моток проволоки нужно разрезать на
т. е моток проволоки нужно разрезать на 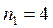 части.
части.
Тогда 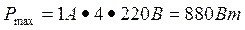 .
.
Критерии оценивания (по 1 баллу).
1. Записана формула площади с анализом max значения.
2. Выяснение условий минимальности R. (2 балла).
3. Учёт max значения тока в проволоке.
4. Определения числа кусков, соединённых параллельно.
5. Расчёт max мощности.
4. В калориметр с водой при температуре 20°С опустили тело массой 152 г при температуре 100°С. Температура поднялась до 30°С. Не вынимая тело, в сосуд налили 100 г воды при 100°С, при этом температура поднялась до 60°С. Определите удельную теплоемкость тела. Теплоемкостью калориметра не пренебрегать. Удельная теплоемкость воды 4200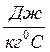 .
.
Решение
Калориметр с водой получают количество теплоты, равное 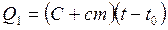 , где С – теплоемкость калориметра, c, m – удельная теплоемкость и масса воды, находящейся в калориметре. Тело, опущенное в воду, отдает количество теплоты, равное
, где С – теплоемкость калориметра, c, m – удельная теплоемкость и масса воды, находящейся в калориметре. Тело, опущенное в воду, отдает количество теплоты, равное 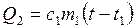 , где c1, m1, t1 — удельная теплоемкость, масса и начальная температура тела. Запишем уравнение теплового баланса для первого процесса Q1+Q2=0, т. е.
, где c1, m1, t1 — удельная теплоемкость, масса и начальная температура тела. Запишем уравнение теплового баланса для первого процесса Q1+Q2=0, т. е.
(C+cm)(t-t0) = c1 m1 (t-t1). Отсюда можно выразить C+cm=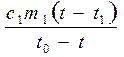 (1).
(1).
После доливания горячей воды, которая отдаст количество теплоты, равное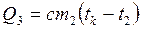 , где m2, t2 — масса и начальная температура горячей воды, а tk – конечная температура, содержимое калориметра получит количество теплоты, равное
, где m2, t2 — масса и начальная температура горячей воды, а tk – конечная температура, содержимое калориметра получит количество теплоты, равное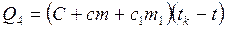 . Запишем уравнение теплового баланса для второго процесса Q3+Q4=0, т. е.
. Запишем уравнение теплового баланса для второго процесса Q3+Q4=0, т. е. 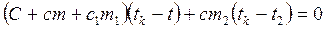 (2).
(2).
Подставив первое выражение во второе, получим расчетную формулу:
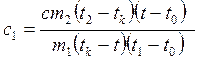 . При расчете получим:
. При расчете получим: 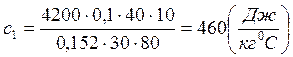
Критерии оценивания (по 1 баллу).
1. Записаны уравнения количеств теплоты, которые получат калориметр с водой, и отдаст тело, опущенное в воду.
2. Записано уравнение количества теплоты, которое отдаст после доливания горячая вода.
3. Записано уравнение количества теплоты, которое получит после доливания горячей воды содержимое калориметра.
4. Записано уравнение теплового баланса для первого и второго процессов.
5. Получена расчетная формула.
6. Произведен расчет по формуле.
11 класс
1. Груз массой m лежит на клине с углом наклона 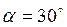 . С каким ускорением необходимо перемещать клин по горизонтальной поверхности, чтобы груз начал скользить по клину вверх? Коэффициент трения между грузом и поверхностью клина равен 0,1.
. С каким ускорением необходимо перемещать клин по горизонтальной поверхности, чтобы груз начал скользить по клину вверх? Коэффициент трения между грузом и поверхностью клина равен 0,1.
Решение
До скольжения сила трения покоя направлена вверх вдоль наклонной плоскости и не превышает максимального значения силы трения покоя, т. е. 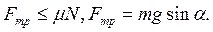
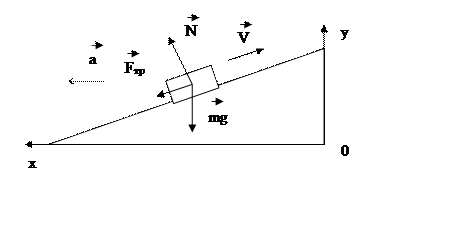

Найдем значение ускорения а0. при котором груз еще не скользит по клину вверх при перемещении клина с ускорением по горизонтальной поверхности, По второму закону Ньютона:
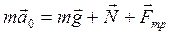 .
.
Перейдя к проекциям на координатные оси и дописав уравнение для силы трения, получим:
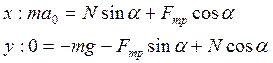
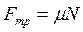
Решая полученную систему уравнений, найдем а0:
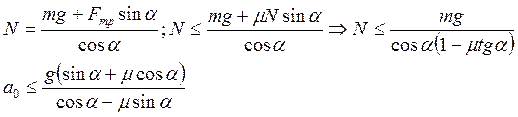
Скольжение начнется при 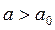 , т. е.
, т. е.
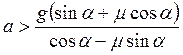
При расчете получим: 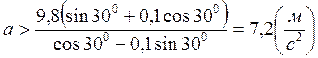
Критерии оценивания (по 1 баллу).
1. Представлен чертеж с указанием сил и выбором системы отсчета.
2. Определены условия скольжения и покоя, значение силы трения.
3. Записан второй закон Ньютона в векторной форме.
4. Записан второй закон Ньютона в проекциях на координатные оси.
5. Решение полученной системы уравнений и неравенств.
6. Произведен расчет по формуле.
2. С одноатомным газом совершен цикл, изображенный на рисунке 2.
Определите КПД цикла,
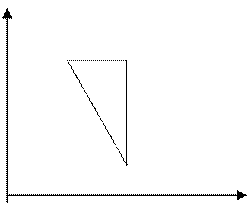 P
P
5p0 2 3
p0 1
0 V0 2V0 V
Рис. 2
Решение
КПД цикла определяется по формуле: 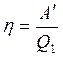 .
.
Работа, совершенная газом, численно равна площади треугольника: 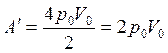 .
.
Найдём, в каких процессах газ получает тепло:
1-2: 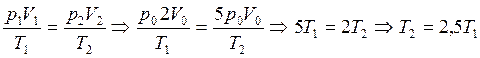 , т. е.
, т. е. 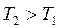 .
.
Температура возрастает, следовательно, Q поглощается.
2-3: p – const, V3>V2![]() T3>T2 – Q поглощается.
T3>T2 – Q поглощается.
3-1: V – const, p3>p1 ![]() T3>T1 — Q выделяется.
T3>T1 — Q выделяется.
Таким образом, тепло полученное газом, равно: 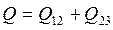 .
.
Из первого закона термодинамики
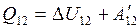 и
и 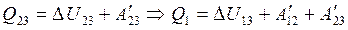 .
.
Найдем изменение внутренней энергии одноатомного газа в процессе 1 — 2 — 3: 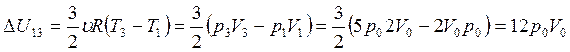 , т. к. по закону Менделеева-Клапейрона
, т. к. по закону Менделеева-Клапейрона 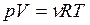 .
.
Работа, совершенная газом на участке 1 — 2, численно равна площади трапеции
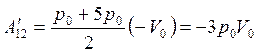 ,
,
а на участке 2-3 равна площади прямоугольника 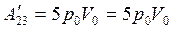 ,
,
Тогда 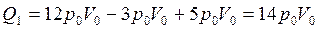 и
и
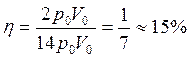 .
.
Критерии оценивания (по 1 баллу).
1. Анализ процессов с указанием направления теплопередачи.
2. Применение 1-го закона термодинамики для нахождения Q12 и Q23.
3. Нахождение изменения внутренней энергии в этих процессах.
4. Нахождение работы газа ![]() ,
, ![]() .
.
5. Определение работы, совершённой газом в циклическом процессе.
6. Нахождения количества теплоты, полученной газом и расчёт КПД цикла.
3. Для зарядки конденсатора собрали электрическую цепь по следующей схеме (рис.3) и замкнули ключ. После зарядки энергия, запасенная конденсатором, оказалась равной 5 Дж. Сколько энергии выделилось в виде тепла в цепи?
 E
E
R K
C
Рис. 3
Решение
После зарядки напряжение на конденсаторе равно U=E., а заряд q=cU=cE. Тогда энергия, запасенная конденсатором, будет равной .
Источник тока совершил работу по перемещению заряда 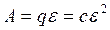 .
.
С другой стороны, по закону сохранения энергии 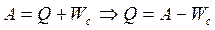 — энергии, выделившаяся в виде тепла в цепи. Подставляя соответствующие значения в формулу, получим
— энергии, выделившаяся в виде тепла в цепи. Подставляя соответствующие значения в формулу, получим 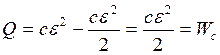 .
.
Таким образом 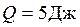 .
.
Критерии оценивания (по 1 баллу).
1. Формула энергии конденсатора.
2. Определение соотношения между напряжением на конденсаторе после окончания зарядки и E источника тока.
3. Применение закона сохранения энергии в виде A=Q+Wc.
4. Определение полной работы источника тока при зарядке.
5. Определение заряда конденсатора.
6. Определение количества теплоты, выделенной в цепи.
4. Моток проволоки имеет сопротивление 1000 Ом. Максимальный ток, который выдерживает данная проволока, равен 1А. Какой максимальной тепловой мощности нагреватель можно изготовить из данной проволоки, если он будет включаться в розетку с напряжение 220В.
Решение
Максимальная тепловая мощность нагревателя опреднляется по формуле: 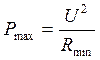 , Минимальное сопротивление нагреватель будет иметь, если проводники, из которых он состоит соединить параллельно, т. е.
, Минимальное сопротивление нагреватель будет иметь, если проводники, из которых он состоит соединить параллельно, т. е. 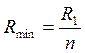 , где R1 – сопротивление каждого из n кусков проволоки, которые соединены параллельно. Если моток разрезали на n частей, то сопротивление одной проволоки равно
, где R1 – сопротивление каждого из n кусков проволоки, которые соединены параллельно. Если моток разрезали на n частей, то сопротивление одной проволоки равно 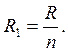 Тогда
Тогда 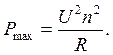 Т. к. извесен максимальный ток, который выдерживает данная проволока, то сила тока в нагревателе будет равна
Т. к. извесен максимальный ток, который выдерживает данная проволока, то сила тока в нагревателе будет равна 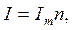 и
и 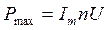 , тогда
, тогда 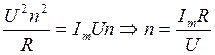 .
.
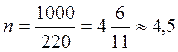 т. е моток проволоки нужно разрезать на
т. е моток проволоки нужно разрезать на 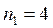 части.
части.
Тогда 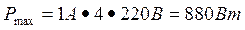 .
.
Критерии оценивания (по 1 баллу).
1. Записана формула площади с анализом max значения.
2. Выяснение условий минимальности R. (2 балла).
3. Учёт max значения тока в проволоке.
4. Определения числа кусков, соединённых параллельно.
5. Расчёт max мощности.


