Основы теоретической физики

Введение

Данное учебно-методическое пособие предназначено для студентов 4 курса специальности «Физика и Информатика» физико-математического факультета. В пособии приведены упражнения, выполнение которых предусмотрено на практических занятиях и в процессе самостоятельной подготовки к ним. Краткие теоретические сведения и алгоритмы выполнения некоторых упражнений облегчают самостоятельное выполнение упражнений.

Большая часть практических занятий рассчитана на 2 часа, однако на изучение материала некоторых тем оставлено больше времени – 4 часа.

Часть предлагаемых к решению задач включена в практическую часть экзамена.

Список рекомендуемой литературы

Основная литература

1.  Матвеев А. Н. Электричество и магнетизм: Учеб пособие для студентов вузов. / А. Н. Матвеев; МГУ им. А. В. Ломоносова. – М.: Оникс, 21 век; Мир и образование, 2005.

2.  Maтвeeв А. Н. Электродинамика и теория относительности. / А. Н. Матвеев. – М.: Высшая школа. – 1964.

3.  Тамм И. Е. Основы теория электричества. /И. Е. Тамм. – М.: Наука, 1976.

Дополнительная литература

4.  Ландау Л. Д. Краткий курс теоретической физики. / Л. Д. Ландау, Е. М. Лифшиц. – М.: Наука, 1972.

5.  Гершензон Е. М. Электродинамика. Учеб. пособие для студ. пед. вузов. / Е. М. Гершензон, Н. Н. Малов, А. Н. Мансуров.– М.: Академия, 2002.

6.  Наумов А. Н. Электродинамика: Учеб. пособие./ А. И. Наумов. – М.: Прометей, 1989.

7.  Компанеец А. С. Курс теоретической физики. / А. С. Компанеец. – М. Просвещение, 1972.

8.  Савельев И. В. Основы теоретической физики: Учебник для студентов нетеор. спец вузов. / И. В. Савельев. – СПб: Лань. – Т1: Механика. Электродинамика. – 2005. – 496 с.

Практическое занятие №1

Расчет напряженности электрического поля

Краткие теоретические сведения

Напряженность электрического поля элементарного заряда рассчитывается по формуле

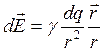, (1.1)

где – коэффициент, зависящий от выбора системы единиц, – радиус-вектор, проведенный из в точку наблюдения (точку, в которой мы рассчитываем электрическое поле). Заметим, что в случае вектор напряженности электрического поля сонаправлен с радиус-вектором (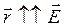), иначе – .

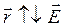Если поле создается несколькими зарядами, то напряженность этого поля находим суммированием

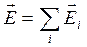, (1.2)

где – вектор напряженности электрического поля -го заряда в точке наблюдения. Приведенная выше формула является математической записью принципа суперпозиции: напряженность поля любого числа зарядов равна сумме напряженностей полей каждого из зарядов при отсутствии всех других.

Если заряд непрерывно распределен по линии, поверхности или объему, напряженность электрического поля рассчитывается с помощью интегрирования (соответственно по линии, поверхности или объему):

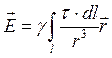, (1.3)

,(1.4)

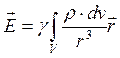, (1.5)

где , , и – линейная, поверхностная и объемная плотности заряда, – радиус-вектор, проведенный от элемента линии (поверхности, объема) в точку наблюдения.

В соответствии с теоремой Гаусса поток вектора напряженности электрического поля через замкнутую поверхность равен отношению заряда, находящегося внутри этой поверхности, к электрической постоянной , то есть

. (1.6)

На границе раздела двух диэлектриков тангенциальные (параллельные касательной к поверхности в данной точке) составляющие вектора напряженности электрического поля непрерывны, а нормальные составляющие терпят разрыв

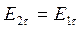, (1.7)

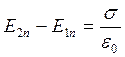, (1.8)

где – поверхностная плотность заряда на границе раздела диэлектриков.

Литература: [1], глава 2, §13;[3], глава 1, §2, 3.

Темы для развернутых ответов

1.  Напряженность электрического поля. Расчет напряженности по определению.

2.  Физическая теорема Гаусса и ее применение для расчета напряженности электрического поля.

3.  Граничные условия для вектора напряженности электрического поля.

Основной блок задач

1.  Дана бесконечная нить, заряженная с поверхностной плотностью заряда . Точка наблюдения находится на расстоянии от нити. Рассчитайте напряженность электрического поля в данной точке.

2.  Дана бесконечная плоскость, равномерно заряженная по поверхности с плотностью заряда . Найдите напряженность электрического поля в точке наблюдения , не принадлежащей плоскости. Попытайтесь выполнить решение вторым способом – с опорой на теорему о граничном условии.

3.  По шару радиуса равномерно распределен заряд с плотностью . Рассчитайте напряженность электрического поля данного шара.

4.  По поверхности сферы радиуса равномерно распределен заряд с плотностью . Рассчитайте напряженность электрического поля данной сферы.

5.  Дана полусфера, равномерно заряженная по поверхности с плотностью заряда . Найдите напряженность электрического поля в центре полусферы.