| Параметрические системы с одной степенью свободы

Решение будем искать в виде (3.15), тогда, вводя t1 = t + q, получаем следующие укороченные уравнения

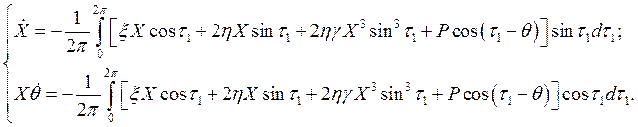
После интегрирования имеем

(4.22)

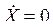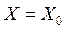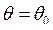Стационарные решения находят из укороченных уравнений при условии, что амплитуда и фазовый сдвиг не меняются: , или , , т. е. из системы уравнений

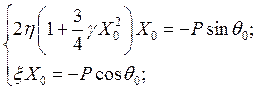
возводя левые и правые части этих уравнений в квадрат и складывая их, получим уравнение

;

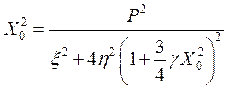оно представляет собой уравнение резонансной кривой для добротного колебательного контура с нелинейным сопротивлением.

При большой нелинейности нельзя предполагать, что решение близко к гармоническому. Мы предполагаем, что есть третья гармоника, т. е. если w1 — частота внешнего воздействия, то 3w1 » w0. Настраиваем контур на эту гармонику и ищем решение (4.20) методом ММА в виде

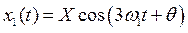полагая, что

, .

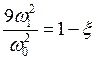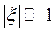Результат получается достаточно близким к тому, который даёт метод гармонического баланса.

Полученные выше укороченные уравнения позволяют найти не только стационарные амплитуду и фазу вынужденного колебания, но в принципе и закон установления стационарного процесса путём интегрирования системы укороченных уравнений (4.22). В этом, в частности, заключается большая эффективность метода ММА по сравнению с методом гармонического баланса, дающего в принципе только стационарные значения амплитуд.

Тема 5. Параметрические системы с одной степенью свободы

Если внешнее воздействие меняет параметры системы, а не координаты, то оно называется параметрическим. В этой теме будут рассмотрены колебательные системы, в которых один из параметров меняется во времени.

Исследуя только системы с одной степенью свободы, мы ограничим свою задачу рассмотрением лишь периодических изменений или, как часто говорят, случаем периодической модуляции параметра.

5.1. Параметрическое воздействие на колебательный контур, передача энергии

Рассмотрим простейший линейный RLC контур. Пусть ёмкость конденсатора контура меняется во времени с помощью какого-то внешнего устройства по изображённому на графике закону (рис. 32). Предположим, кроме того, что заряд на конденсаторе меняется по закону, близкому к гармоническому, т. е.

, где .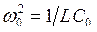

Рис. 32. Графики периодического изменения q (сверху) и C (снизу) при параметрическом воздействии.

Пусть под воздействием внешнего источника управляющего напряжения ёмкость конденсатора меняется с частотой 2w0 , где w0 — частота собственных колебаний. Заряд q при скачкообразном изменении ёмкости не меняется, ибо является инерционной величиной. Пусть частотные и фазовые соотношения между q(t) и C(t) таковы, что ёмкость конденсатора уменьшается каждый раз точно в те моменты времени, когда заряд на ёмкости проходит через экстремум (рис. 32). При этом вложение энергии в систему будет максимальным, так как при раздвижении обкладок конденсатора для уменьшения C совершается максимальная работа против электростатических сил притяжения между пластинами.

Рассчитаем приращение энергии конденсатора DN, которое получается в момент скачка ёмкости:

.

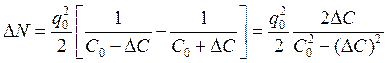Считая, что DC << C0, можно записать

,

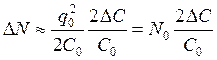где N0 характеризует энергию, запасённую в конденсаторе до скачка ёмкости (энергия без модуляции). Если ввести индекс модуляции m:

,

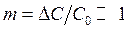то приращение колебательной энергии в контуре после одного скачкообразного уменьшения ёмкости равняется DN = N02m. Отметим, что изменение колебательной энергии DN в контуре при параметрическом воздействии пропорционально самой энергии N0, запасённой в системе.

В соответствии с выбранным фазовым соотношением между q и C следующее скачкообразное изменение ёмкости не вызовет изменения энергии, так как в соответствующие моменты времени начальная энергия равна нулю (q = 0), как показано на рис. 32. Таким образом, энергия будет увеличиваться при уменьшении ёмкости. За период энергия вкладывается два раза и тогда общее приращение энергии в системе за период

.

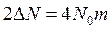Теперь определим потери в контуре. Энергия, теряемая системой за период T, равна

.

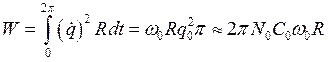Условием установившихся колебаний будет равенство: W = 2DN. Если 2DN > W, то подкачка энергии в систему превышает потери в ней и происходит увеличение амплитуды колебаний. Условие нарастания амплитуды принимает вид:

,

(5.1)

где d — логарифмический декремент затухания контура. Процесс возбуждения колебаний за счёт периодического изменения энергоёмкого параметра колебательной системы мы будем называть параметрическим возбуждением колебаний или параметрическим резонансом; а величина m0 в соотношении (5.1) называется порогом параметрического возбуждения.

Примером параметрического воздействия на колебательную систему может также служить маятник с переменной длиной нити.

В рассмотренном примере параметр изменялся дважды за период возбуждаемых колебаний. Но можно производить вложение энергии за счёт изменения параметра один раз за период, два раза за три периода и т. д. В общем случае условие параметрического возбуждения имеет вид:

,

(5.2)

где n = 1, 2, …, w1 — частота возбуждающей силы (частота изменения параметра), w — частота собственных колебаний (частота возбуждаемых колебаний). При этом, конечно, энерговложение в возбуждаемую систему за период будет тем меньше, чем больше n.

Процесс колебаний в линейной параметрической системе с одной степенью свободы в общем случае описывается простым линейным уравнением с переменными коэффициентами

,

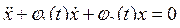где j1 и j2 — периодические функции времени. Это уравнение решается подстановкой

,

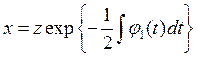которая преобразует его в уравнение Хилла

,

(5.3)

где

.

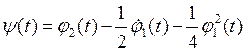В частном случае, если модуляция параметра происходит по гармоническому закону, а система без потерь, то колебательный процесс в ней описывается уравнением Матье

.

(5.4)

Общее решение уравнения (5.4) имеет вид

;

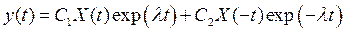здесь X(t) — ограниченные периодические функции с периодом 2p/w1, равным периоду изменения параметра, и l — комплексная величина, называемая характеристическим показателем. Полный анализ решений математически довольно сложен и для линейных случаев, а тем более и для нелинейных задач. Поэтому он сводится к нахождению таких областей значений соотношения частот 2w0/w1 и глубин модуляции m, для которых имеются комплексные значения l1 и l2. Тогда в системе могут происходить нарастающие колебания, т. е. возникает параметрический резонанс.

Если под параметрическим воздействием находится линейная система с диссипацией, то (5.4) примет вид

.

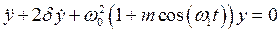Области параметрического возбуждения для такой системы установил М. А. Леонтович. Результаты его расчётов в виде графика показаны на рис. 33. Заштрихованные области соответствуют нарастающему процессу с частотой w = nw1/2 » w0 (n = 1, 2, …). Вне этих областей — затухающий процесс колебаний. На границе областей имеет место баланс энергии.

Рис. 33. Области параметрического возбуждения для системы с затуханием.

Из графиков видно, что для заданного значения m0 ширина области параметрического возбуждения для разных номеров n различна для систем с разной диссипацией, так как чем больше потери в системе, тем больше угол наклона.

Есть одна интересная деталь, которая отличает параметрическое возбуждение от силового. При силовом воздействии в системе с потерями даже в резонанс установится конечная амплитуда вынужденных колебаний, которая будет пропорциональна добротности системы. Почему такое происходит? Нетрудно показать, что при силовом воздействии, подкачка энергии

от внешней системы линейно зависит от амплитуды колебаний, а потери зависят квадратично. При малых амплитудах колебаний подкачка превосходит потери. Затем начинают нарастать вынужденные колебания, начинают нарастать потери и при некоторой амплитуде вынужденных колебаний потери сравниваются с подкачкой и стабилизируется амплитуда. При параметрическом возбуждении и потери, и подкачка линейно зависят от амплитуды параметрического воздействия. Таким образом, если возникло параметрическое возбуждение, т. е. подкачка превзошла потери, то подкачка будет превосходить потери при любой амплитуде колебаний (в линейной параметрической системе стабилизация амплитуды вынужденных колебаний не возможна, даже не смотря на потери).

Нелинейные параметрические системы даже М. А. Лентовичу оказались не по зубам, но нам придётся и с ними иметь дело. Для их анализа существуют приближённые методы, например, метод гармонического баланса. Для простоты рассмотрим консервативную систему, состоящую из индуктивности и конденсатора с сегнетоэлектриком. Пусть в этой системе за нелинейность отвечает конденсатор, а за периодическое изменение параметра отвечает индуктивность

, .

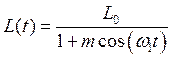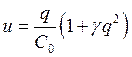Пусть нелинейность слабая и собственные колебания в системе происходят с частотой близкой к частоте свободных колебаний, т. е. 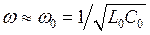; а параметрическое воздействие происходит с частотой w1 = 2w0. Тогда уравнение колебаний в системе

,

(5.5)

где f(q) = uC0 = q + gq3.

Будем, в соответствии с методом гармонического баланса, искать решение в виде гармоники с основной частотой w. Рассматриваем установившийся процесс

,

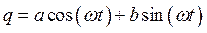тогда, подставив это решение в (5.5), получим:

.

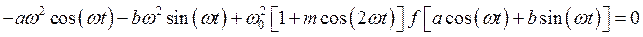Разлагая f(q) в ряд Фурье и сохраняя лишь члены с cos(wt) и sin(wt), находим уравнение, из которого, группируя коэффициенты при cos(wt) и sin(wt), получим систему двух уравнений

; .

(5.6)

При замене wt = t, имеем

;

.

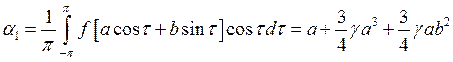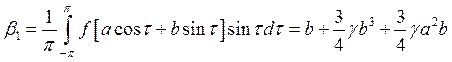Отсюда находим амплитуду возможного стационарного решения

.

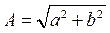Таким образом, (5.6) приводим к виду

; .

(5.7)

По сути, мы получили линейную систему уравнений. Относительно a и b мы видим первое решение — тривиальное. Это решение соответствует состоянию покоя; такое состояние является возможным равновесным состоянием системы, но оно нам не интересно. Куда более интересно нетривиальное решение.

Одновременно a и b не могут быть не равны нулю (a ¹ 0, b ¹ 0), так как в этом случае мы можем просто-напросто на них сократить оба уравнения и тогда мы придём к несовместным уравнениям. Поэтому возможны только случаи, когда один из коэффициентов равен, а другой отличен от нуля. Принимая a ¹ 0, b = 0, а потом a = 0, b ¹ 0, получаем в общем виде

,

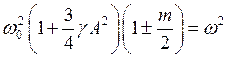где верхний знак соответствует первому случаю, а нижний — второму. Отсюда находим амплитуду колебаний

.

(5.8)

Как видно значение A тем больше, чем меньше коэффициент нелинейности g, и когда нелинейность полностью отсутствует, амплитуда колебаний уходит в бесконечность. Нужно отметить, что амплитуда A реальна (A2 > 0), поэтому условию установившихся колебаний (когда порог возбуждения превзойдён) соответствует дробь (в скобках) больше единицы. Откуда получим условие параметрического возбуждения
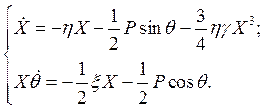
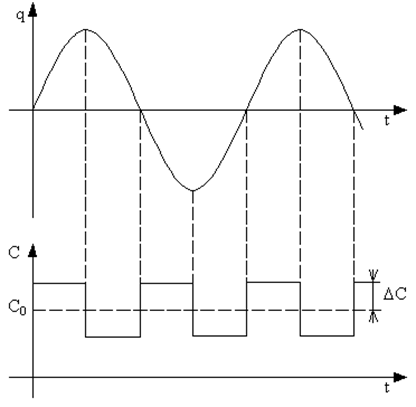
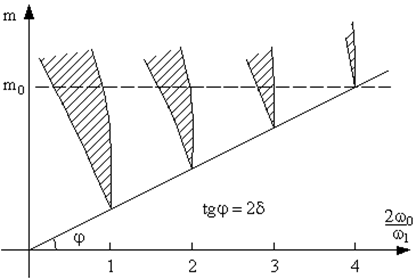
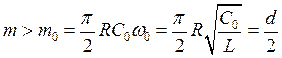
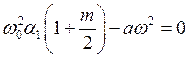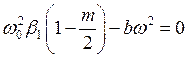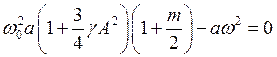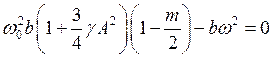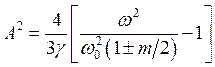