Переменное электромагнитное поле
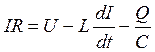 , ()
, ()
откуда получаем дифференциальное уравнение
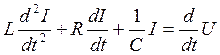 , ()
, ()
которое позволяет определить силу тока в цепи как функцию времени.
Темы для развернутых ответов
1. Условия квазистационарности и их физический смысл.
2. Квазистационарные явления в цепи переменного тока.
Литература: [1], глава 8, §48; [3], глава 6, §76-78.
Основной блок задач
1. Ток в колебательном контуре меняется по закону 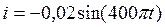 (ток измеряется в А). Найдите период колебаний, емкость контура, максимальную разность потенциалов на обкладках конденсатора, максимальную энергию магнитного и электрического полей, если индуктивность контура 1 Гн.
(ток измеряется в А). Найдите период колебаний, емкость контура, максимальную разность потенциалов на обкладках конденсатора, максимальную энергию магнитного и электрического полей, если индуктивность контура 1 Гн.
2. В начальный момент времени в цепь, состоящую из последовательно соединенных сопротивления ![]() и индуктивности
и индуктивности ![]() , включают ЭДС постоянной величины
, включают ЭДС постоянной величины ![]() . Найдите зависимость силы тока от времени. Выполните данную задачу для выключения постоянной ЭДС величины
. Найдите зависимость силы тока от времени. Выполните данную задачу для выключения постоянной ЭДС величины ![]() .
.
3. Постоянное напряжение ![]() включают в цепь, состоящую из последовательно соединенных сопротивления
включают в цепь, состоящую из последовательно соединенных сопротивления ![]() и емкости
и емкости ![]() . Найдите зависимость силы тока от времени в данной цепи. Выполните задачу для выключения постоянного напряжения.
. Найдите зависимость силы тока от времени в данной цепи. Выполните задачу для выключения постоянного напряжения.
Дополнительный блок задач
4. К цепочке из последовательно соединенных сопротивления ![]() и емкости
и емкости ![]() прикладывается прямоугольный импульс напряжения
прикладывается прямоугольный импульс напряжения 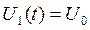 при
при 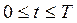 и
и 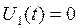 при
при ![]() и
и ![]() , где
, где ![]() – длительность импульса. Найдите зависимость напряжения на сопротивлении
– длительность импульса. Найдите зависимость напряжения на сопротивлении ![]() от времени. Учтите отношение длительностью импульса и временем релаксации.
от времени. Учтите отношение длительностью импульса и временем релаксации.
5. В цепь, состоящую из последовательно соединенных сопротивления ![]() и индуктивности
и индуктивности ![]() , включают ЭДС
, включают ЭДС ![]() . Определите силу тока в цепи. При каком значении начальной фазы
. Определите силу тока в цепи. При каком значении начальной фазы ![]() переходные явления в цепи не возникают.
переходные явления в цепи не возникают.
6. Покажите, что синусоидальное изменение силы тока удовлетворяет уравнению ().
Практическое занятие №13
Переменное электромагнитное поле
Краткие теоретические сведения
Система уравнений Максвелла для переменных полей включает в себя следующие уравнения:
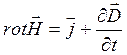 ; (13.1)
; (13.1)
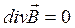 ; (13.2)
; (13.2)
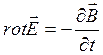 ; (13.3)
; (13.3)
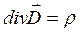 ; (13.4)
; (13.4)
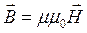 ; (13.5)
; (13.5)
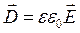 ; (13.6)
; (13.6)
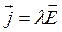 . (13.7)
. (13.7)
Эти уравнения позволяют описывать все макроскопические электромагнитные явления.
Плотность энергии электромагнитного поля рассчитываем по формуле
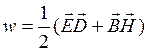 , (13.8)
, (13.8)
энергия некоторого объема рассчитывается интегрированием.
Плотность потока энергии сквозь поверхность, ограничивающую некоторый объем равна 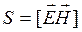 – вектор Пойтинга.
– вектор Пойтинга.
Изменение энергии электромагнитного поля в объеме происходит за счет работы токов проводимости (в единицу времени) в этом объеме и потока энергии сквозь поверхность, ограничивающую объем –
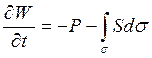 , (13.9)
, (13.9)
где ![]() – поверхность, ограничивающая данный объем.
– поверхность, ограничивающая данный объем.
Вопросы для развернутых ответов
1. Система уравнений Максвелла в дифференциальной и интегральной формах. Пояснить значение каждого из уравнений.
2. Система уравнений Максвелла в вакууме.
Уточнить !!!Литература: [1], глава 9, §61-62; [3], глава 7, §91-98.
Основной блок задач
1. Докажите, что электрическая энергия, поглощаемая в проводнике при прохождении по нему тока и идущая на нагревание проводника, поступает в него из внешнего электромагнитного поля.
2. Ток, протекающий по обмотке длинного прямого соленоида, достаточно медленно увеличивают. Покажите, что скорость возрастания энергии магнитного поля соленоида равна потоку вектора Пойтинга через его боковую поверхность.
Дополнительный блок задач
3. Плоский конденсатор с круглыми параллельными пластинами медленно заряжают. Показать, что поток вектора Пойтинга через боковую поверхность конденсатора равен приращению энергии конденсатора в единицу времени.
4. Показать, что на границе раздела двух сред нормальные составляющие вектора Пойтинга не терпят разрыва, то есть 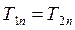 . Что можно сказать о тангенциальных составляющих этого вектора?
. Что можно сказать о тангенциальных составляющих этого вектора?
Практическое занятие №14
Электромагнитные волны
Краткие теоретические сведения
Не начать ли просто с волнового уравнения? Импульс волны?
Записывая уравнения Максвелла для однородной нейтральной (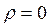 ) непроводящей (
) непроводящей (![]() ) среды с постоянными проницаемостями
) среды с постоянными проницаемостями ![]() и
и ![]() , получим
, получим
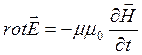 , (14.1)
, (14.1)
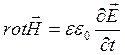 . (14.2)
. (14.2)
Применяя к первому из приведенных уравнений оператор ![]() , получим
, получим
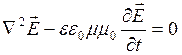 . (14.3)
. (14.3)
Аналогично для напряженности магнитного поля
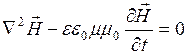 . (14.4)
. (14.4)
Уравнение такого вида называется волновым, а удовлетворяющая ему функция описывает некоторую волну.
Фазовая скорость распространения электромагнитной волны
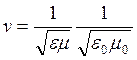 , (14.5)
, (14.5)
для вакуума получим
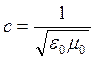 . (14.6)
. (14.6)
Рассмотрим распространение плоской электромагнитной волны вдоль оси ![]() некоторой системы координат. Если электрическое поле направлено вдоль оси
некоторой системы координат. Если электрическое поле направлено вдоль оси ![]() , то магнитное поле – вдоль оси
, то магнитное поле – вдоль оси ![]() . Решением волнового уравнения является функция
. Решением волнового уравнения является функция
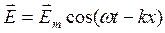 (14.7)
(14.7)
для электрического поля и
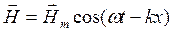 (14.8)
(14.8)
для магнитного, где ![]() – частота волны,
– частота волны, 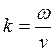 – волновое число. Векторы напряженности магнитного и электрического полей в волне колеблются в одной фазе, одновременно достигая максимума или минимума. Амплитуды напряженностей связаны соотношением
– волновое число. Векторы напряженности магнитного и электрического полей в волне колеблются в одной фазе, одновременно достигая максимума или минимума. Амплитуды напряженностей связаны соотношением
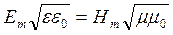 . (14.9)
. (14.9)
Вопросы для развернутых ответов
1. Покажите, что уравнение электромагнитной волны удовлетворяет уравнениям Максвелла (на примере электрического или магнитного полей в вакууме).
2. Получите волновое уравнение для напряженности электрического поля из системы уравнений Максвелла в вакууме.
Литература: [1], глава 9, §61-62; [3], глава 7, §91-98.
Основной блок задач
1. Электромагнитная волна распространяется в вакууме вдоль оси Х. В точке А в некоторый момент времени модуль плотности тока смещения 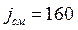 мкА/м. Найдите в этой же точке в тот же момент времени модуль производной
мкА/м. Найдите в этой же точке в тот же момент времени модуль производной ![]() .
.
2. Исходя из уравнений Максвелла, покажите, что для плоской электромагнитной волны, распространяющейся в вакууме в направлении оси Х, справедливы соотношения 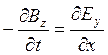 ,
, 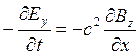 .
.
3. В вакууме распространяется плоская электромагнитная волна частоты ![]() , для которой среднее значение плотности потока энергии равно Т. Найдите амплитудное значение плотности тока смещения в этой волне.
, для которой среднее значение плотности потока энергии равно Т. Найдите амплитудное значение плотности тока смещения в этой волне.
4. Импульс, переносимый плоской электромагнитной волной через площадку в 10 см2 за 5 с, равен 10-2 кг∙м/с. Определите интенсивность волны.
5. Какое давление оказывает плоская электромагнитная волна на преграду, коэффициент отражения которой равен 0,9, расположенную под углом 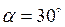 к направлению распространения волны, если амплитуда напряженности магнитной составляющей волны
к направлению распространения волны, если амплитуда напряженности магнитной составляющей волны ![]() ?
?
6. Плоская гармоническая электромагнитная волна имеет следующие параметры: 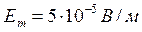 ,
, 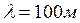 . Какая энергия переносится волной за 10 минут через площадку 1 м2, расположенную перпендикулярно скорости распространения волны?
. Какая энергия переносится волной за 10 минут через площадку 1 м2, расположенную перпендикулярно скорости распространения волны?
Дополнительный блок задач
7. Считая, что частица имеет форму шарика и поглощает весь падающий на нее свет, найти радиус частицы, при котором гравитационное притяжение ее к Солнцу будет компенсироваться силой светового давления. Мощность светового излучения Солнца равна 4∙1026 Вт, а плотность частицы 1,0 г/см3.
8. Заряженная частица движется вдоль оси У по закону 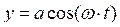 , а точка наблюдения находится на оси Х на расстоянии
, а точка наблюдения находится на оси Х на расстоянии ![]() от частицы
от частицы 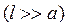 . Найдите отношение плотностей потока электромагнитного излучения в точке наблюдения в моменты, когда координаты частицы равны 0 и
. Найдите отношение плотностей потока электромагнитного излучения в точке наблюдения в моменты, когда координаты частицы равны 0 и ![]() . Рассчитайте это отношение, если
. Рассчитайте это отношение, если ![]() =2,01∙108 с-1 и
=2,01∙108 с-1 и ![]() =50м. Запаздыванием пренебречь.
=50м. Запаздыванием пренебречь.
9. Нерелятивистский протон влетел по нормали в полупространство с поперечным однородным магнитным полем, индукция которого 1,0 Тл. Найти отношение энергии, потерянной протоном на излучение за время его движения в поле, к его первоначальной кинетической энергии.
10.Найти мощность излучения нерелятивистской частицы массой ![]() и зарядом
и зарядом ![]() , движущейся по круговой орбите радиуса
, движущейся по круговой орбите радиуса ![]() в поле неподвижного точечного заряда
в поле неподвижного точечного заряда ![]() .
.
11.Средняя мощность, излучаемая диполем, равна Р0. Найдите среднюю плотность энергии электромагнитного поля в вакууме в волновой зоне на луче, перпендикулярном оси диполя, на расстоянии r от него.
12.Воздушный промежуток между внешним и внутренним проводниками коаксиального кабеля заполнили некоторым диэлектриком, вследствие чего скорость распространения электромагнитной волны в кабеле уменьшилась на 25%. Определите относительную электрическую восприимчивость диэлектрика.
Практическое занятие №15
Основы специальной теории относительности
Краткие теоретические сведения
В основе специальной теории относительности лежат два постулата:
1. Принцип относительности – все физические явления (не только механические) протекают одинаково во всех инерциальных системах отсчета, и никакими опытами, проводимыми внутри данной инерциальной системы отчета (ИСО) невозможно обнаружить ее движение относительно других ИСО.


