Погрешности измерений и погрешности средств измерения

ЛАБОРАТОРНАЯ РАБОТА № 3

по дисциплине «Управление, сертификация и инноватика

(Метрология, стандартизация и сертификация)»

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ И ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЯ

СОДЕРЖАНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

1. Погрешности измерений

2. Погрешности средств измерений

Контрольные вопросы Пример решения задачи Варианты задач

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ

Законспектировать:

Ответить на все контрольные вопросы, приведенные в конце лабораторной работы; Составить классификации погрешностей измерений и погрешностей средств измерений.

Знать:

Основные виды погрешностей измерений; основные положения теории погрешностей; Погрешности средств измерений;

Решить:

·  индивидуально каждый студент должен решить все варианты задач.

Оформление отчета:

·  отчет выполняется индивидуально каждым студентом в отдельной тетрадке рукописным способом. Тетрадь начинается с титульного листа, где указаны ФИО студента и группа. Отчет по лабораторной работе начинается с названия и даты выполнения.

1. Погрешности измерений

Рассмотрим основные виды погрешностей измерения. В зависимости от формы выражения различают абсолютную и относительную по­грешности.

Абсолютной называют погрешность измерений, выражен­ную в тех же единицах, что и измеряемая величина. Её определяют как:

D = А — Хист

или

D @ А – Хд

где А — результат измерения;

Хист — истинное значение измеряемой физической величины;

Хд — действительное значение измеряемой величины.

Относительная погрешность измерения (d) представляет собой отношение абсолютной погрешности измерений к истинному (действительному) значению измеряемой величины. Относительную по­грешность в % определяют по формуле:

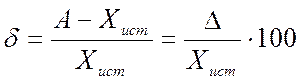
или

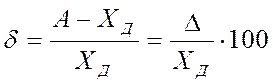
Пример. В результате измерения силы электрического тока в цепи I получен ряд значений: i1 = 0.55 A; i2 = 0.58 A; …in = 0.54 А. Вычислено среднее значение i = 0.56 А.

Погрешности D1 = i1 – i = 0,55-0,56 = -0,01 А; D2= i2 — i=0,58 -0,56=0,02 A;

Dn= in – i = 0,54-0,56 = -0,02 А являются абсолютными по­грешностями измерений.

Приняв в качестве действительного значения среднее значение, т. е. iД = i, определим относительную погрешность отдельного измерения в ряду измерений:

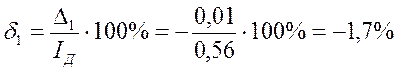
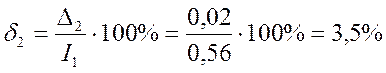
В зависимости от условий и режимов измерения различают стати­ческие и динамические погрешности.

Статической называют погрешность, не зависящую от ско­рости изменения измеряемой величины во времени.

Динамической называют погрешность, зависящую от ско­рости изменения измеряемой величины во времени. Динамическая по­грешность обусловлена инерционностью элементов измерительной цепи средства измерения.

В зависимости от характера проявления, возможностей устранения и причин возникновения различают систематические и случайные по­грешности.

Систематической (Dc) называют составляющую погреш­ности измерения, остающуюся постоянной или закономерно изменяю­щейся при повторных измерениях одной и той же величины.

Причина­ми систематической погрешности могут быть:

— отклонение параметров реального средства измерения от расчет­ных значений, предусмотренных схемой;

— неуравновешенность деталей средства измерений относительно их оси вращения;

— погрешность градуировки или небольшой сдвиг шкалы и др.

Ряд постоянных систематических погрешностей в процессе измере­ния внешне себя не проявляют. Обнаружить их можно в процессе по­верки путем сравнения результатов измерения рабочими средствами и образцовыми.

Случайной называют погрешность измерений, изменяю­щуюся случайным образом при повторных измерениях одной и той же величины.

Случайная погрешность возникает при одновременном воздействии многих источников, каждый из которых сам по себе оказывает незамет­ное влияние на результаты измерений, но суммарное воздействие всех источников может оказаться достаточно сильным.

Как правило, при выполнении измерений случайная и систематиче­ская погрешности проявляются одновременно, поэтому погрешность измерения равна:

.

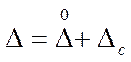Заметим, что случайные погрешности представляют собой погреш­ности, в появлении каждой из которых не наблюдается какой-либо за­кономерности. Случайные погрешности неизбежны и неустранимы. Они всегда присутствуют в результате измерения. Они вызывают рас­сеяние результатов при многократном и достаточно точном измерении одной и той же величины при неизменных условиях, вызывая различие их в последних значащих цифрах.

В основе теории погрешностей лежат два положения, подтвер­жденные практикой:

·  при большом числе измерений случайные погрешности одинако­вого значения, но разного знака встречаются одинаково часто;

· большие по абсолютному значению погрешности встречаются реже, чем малые.

Из первого положения следует важный для практики вывод, что при увеличении числа измерений случайная погрешность результата, полученного из ряда измерений, уменьшается вследствие того, что сумма погрешностей отдельных измерений данного ряда измерений стремится к нулю, т. е.

.

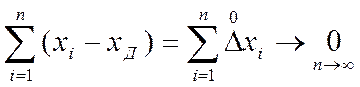В ряду измерений выделяют также грубые погрешности и промахи, которые возникают из-за ошибок и неправильных действий оператора, а также при кратковременных, резких изменениях условий проведения измерений (появление вибрации, поступление хо­лодного воздуха и т. д.).

При автоматических измерениях грубые погрешности и промахи автоматически исключаются в процессе обработки измерительной ин­формации.

2. Погрешности средств измерений.

Отметим, что погрешности изме­рений определяются, главным образом, погрешностями средств изме­рений, но они не тождественны им.

В общем случае погрешность средства измерений (меры измери­тельного преобразователя, измерительного прибора) — это отклонение его реальной функции преобразования от номинальной.

Отклонения реальной характеристики от номинальной, отсчитан­ные вдоль оси Х или оси У, т. е. разности вида Dy = Ур — Ун или Dx = Хр — Хн, есть абсолютные погрешности преобразования, выраженные в единицах величин Х или У (рис. 1).

Мерой точности абсолютная погрешность быть не может, т. к., например, DХ = 0.5 мм при измерении высоты пенного слоя пульпы, равной Х = 200 мм, достаточно мала, а при измерении толщины листа стали, при Х = 1 мм, эта погрешность очень велика.

Абсолютная погрешность измерительного прибора DXП­ — это разность между показанием прибора ХП и истинным (действительным) ХД значением измеряемой величины:

DXП = ХП – ХД.

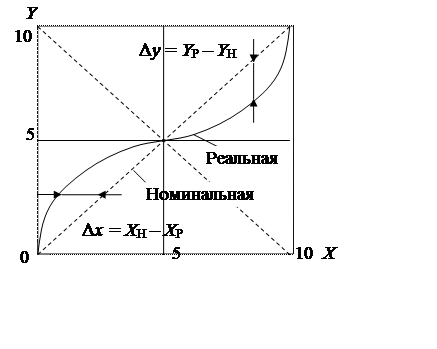
Рис. 1. К пояснению понятия абсолютной погрешности

При этом за действительное значение физической величины при оценке погрешности рабочего средства измерений принимают показа­ния образцового средства измерений, при оценке погрешности образцо­вого средства — показания, полученные с помощью эталонного средства измерений.

Абсолютная погрешность измерительного преобразователя по вхо­ду — это разность между значением величины на входе преобразователя ХВ и истинным (действительным) значением этой величины на входе ХВД. При этом значение величины на входе ХВ определяется по истин­ному (действительному) значению величины на выходе преобразовате­ля с помощью градуировочной характеристики, приписанной преобра­зователю. Таким образом,

DХВ =Х*ВД – ХВД,

где DХВ — погрешность измерительного преобразователя по входу;

Х*ВД — истинное (действительное) значение величины на выходе, найденное по градировочной характеристике преобразова­теля;

ХВД — истинное (действительное) значение преобразуемой величины на входе.

Абсолютная погрешность измерительного преобразователя по вы­ходу — это разность между истинным (действительным) значением ве­личины преобразователя на выходе DХВЫХ. Д и значением величины на выходе Х*ВЫХ. Д, определяемым по истинному (действительному) значе­нию величины на входе с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,

DХВЫХ. П = ХВЫХ. Д — Х*ВЫХ. Д,

где DХВЫХ. П — погрешность измерительного преобразователя по выходу;

ХВЫХ. Д — действительное значение преобразуемой величины на вы­ходе преобразователя;

Х*ВЫХ. Д — действительное значение преобразуемой величины на выхо­де, определяемое по действительному значению ее на входе с помощью градуировочной характеристики.

Абсолютная погрешность — это разность между номинальным значением меры ХН и истинным (действительным) ХД воспроизводимой ею величины, т. е.

DХМ = ХН – ХД,

где  DХМ — абсолютная погрешность мepы;

ХН — номинальное значение мepы;

ХД — действительное значение воспроизводимой мерой величины.

Пример. Погрешность меры длины (линейки) с номинальным значением 100 мм и действительным значением 100,0006 мм равна 0,6 мкм; погрешность меры сопротивления с номинальным значением 1 Ом и действительным значением 1,0001 Ом равна 0,0001 Ом.

Относительная погрешность меры или измерительного прибора (dП) — это отношение абсолютной погрешности меры или изме­рительного прибора к истинному (действительному) значению воспро­изводимой или измеряемой величины.

Относительная погрешность меры или измерительного прибора, в процентах, может быть выражена как:

.

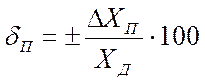Относительная погрешность измерительно­го преобразователя по входу (выходу) — это отноше­ние абсолютной погрешности измерительного преобразователя по вхо­ду (выходу) к истинному (действительному) значению величины на входе (выходе), определяемому по истинному значению величины на входе (выходе) с помощью номинальной характеристики, приписанной преобразователю.

Итак, относительная погрешность средства измерений, выражаемая в процентах или в относительных единицах, не остается постоянной вследствие изменения величин Х или Y по шкале измери­тельного устройства.

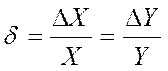
С учетом того, что относительная погрешность средства измерений не остается постоянной, то вводится понятие приведенной погрешно­сти, в общем виде определяемой:

,

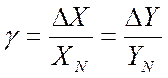где g — приведенная погрешность средства измерений;

XN — нормирующее значение измеряемой величины.

Приведенная погрешность g измерительного прибора — это отношение абсолютной погрешности измерительного прибора DХП к нормирующему значению. Нормирующее значение XN — это условно принятое значение, равное или верхнему пределу измерений*, или диа­пазону измерений**, или длине шкалы***.

Приведенную погрешность обычно выражают в процентах:

.

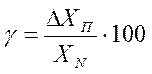Приведенная погрешность позволяет сравнивать по точности при­боры, имеющие разные пределы точности.

Пример. Определить абсолютную, относительную и приведенную погрешности амперметра с диапазоном измерения 0 -15 А при показании его ХП = 12 А и действительном значении измеряемой силы тока ХД = 12,6 А. За нормирующее значение примем верхний предел измерения Xv = 15 А.

Абсолютная погрешность амперметра

DХП = ХП – ХД = 12 — 12,6 = -0,6 А.

Относительная погрешность амперметра

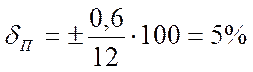
Приведенная погрешность

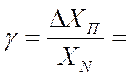
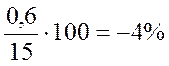
При характеристике погрешностей средств измерений часто пользуются понятием предела допускаемой погрешности измерений.

Предел допускаемой погрешности средства измерений — это наибольшая, без учета знака, погрешность средства измерений, при котором оно может быть признано и допущено к применению. Определение применимо к основной и дополнительной погрешности средств измерений.

Пример. Одинаков ли предел допускаемой относительной погрешности измерения во всех точках шкалы автоматического потенциометра?

Для всех точек шкалы одинаков предел допускаемой абсолютной погрешности, определяемой классом точности средства измерений и диапазоном измерений, а предел допускаемой относительной погрешности измерения зависит от конкретной отметки шкалы, т. е. чем меньше показания прибора по шкале, тем больше относительная погрешность. Вследствие этого верхний предел показаний прибора нужно выбирать таким образом, чтобы значение измеряемой величины находилось в конце шкалы.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений, К этим погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Основная и дополнительная погрешности. Деление это чисто условно. Погрешность средств измерений, определяемую для работающих в нормальных условиях, называют основной погрешностью. Нормальными условиями принято считать условия, когда температура окружающего воздуха t = (20 ± 5) 0C, относительная влажность W = 30 – 80 %, атмосферное давление Р = 630 — 795 мм рт. ст., напряжение питающей сети (U = (220 ± 4,4) В, частота питающей сети f = (50 ± 0,5) Гц. Такие условия выдерживаются в лабораторных условиях при градуировке средств измерений.

В реальных условиях производства эти параметры отличаются от лабораторных. Средства измерения помимо чувствительности к измеряемой величине обладают и некоторой чувствительностью к изменяющимся величинам окружающей среды, что приводит к искажению результатов измерения. Погрешность, появляющуюся у средств измерений, работающих в реальных производственных условиях, называют дополнительной погрешностью. Так же, как основная, дополнительная погрешность нормируется путем указания коэффициентов влияния изменения отдельных влияющих величин на изменение показаний в виде

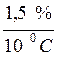α = , α = 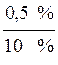· Uпит.

Систематические и прогрессирующие погрешности средств измерений вызываются: первые — погрешностью градуировки шкалы или ее небольшим сдвигом, вторые — старением элементов средства измерения. Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Аддитивные и мультипликативные погрешности. Аддитивная погрешность не зависит от чувствительности прибора и является постоянной для всех значений входной (измеряемой) величины в пределах диапазона измерений (рис.2).

Если реальная характеристика 1 средства измерения смещена относительно номинальной 2 (см. рис. 2) так, что при всех значениях преобразуемой величины Х выходная величина У оказывается больше (или меньше) на одну и ту же величину Δ, то такая погрешность называется аддитивной погрешностью нуля.

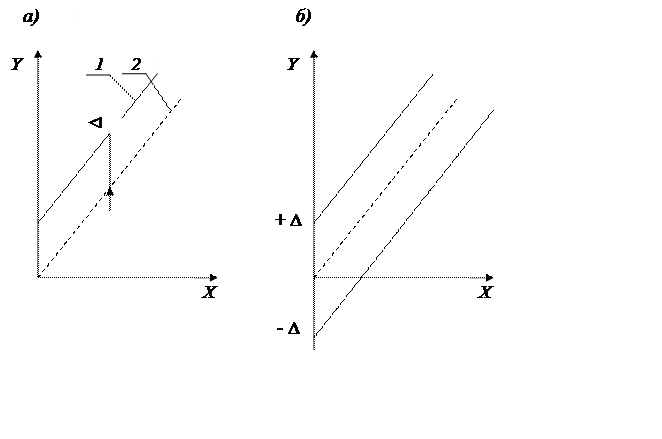
Рис. 2. К пояснению понятия аддитивной погрешности средства измерения

К аддитивным погрешностям средств измерений можно отнести погрешности, вызванные трением в опорах электроизмерительных приборов, погрешность дискретности (квантования) в цифровых приборах. Аддитивная погрешность может носить систематический характер. В этом случае она может быть скорректирована смещением шкалы или нулевого положения указателя.

В случае же, если аддитивная погрешность является случайной, то она не может быть скорректирована, и реальная характеристика средства измерения, смещаясь произвольным образом, но, оставаясь параллельной самой себе, образует полосу погрешностей, ширина которой остается постоянной для любых значений измеряемой величины Х (см. рис. 4.2, б).

Мультипликативная погрешность – это погрешность чувствительности средства измерения. Она может иметь систематическую и случайную составляющие.

Сущность мультипликативной погрешности заключается в том, что если абсолютная погрешность возникает от некоторого независимого от Х изменения чувствительности преобразователя (изменение коэффициента деления делителя, добавочного сопротивления вольтметра и т. д.), то реальная характеристика 1 преобразователя отклоняется от номинальной 2 так, как это показано на рис. 4.3, а, или образует полосу погрешностей (рис. 4.3, б), если это отклонение является случайным.

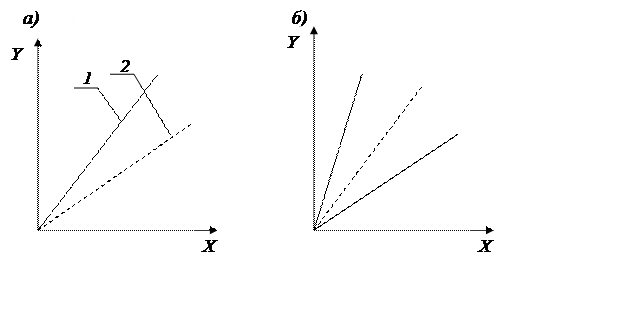
Рис. 4.3. К пояснению понятия мультипликативной
погрешности измерений

КОНТРОЛЬНЫЕ ВОПРОСЫ К ЛАБОРАТОРНОЙ РАБОТЕ:

1. Что такое абсолютная погрешность измерений?

2. Что такое относительная погрешность измерений?

3. Что такое систематическая погрешность измерений?

4. Что такое случайная погрешность измерений?

5. Что такое промах?

6. В чем заключается отличие погрешности измерения от погрешности средства измерения?

7. Что такое абсолютная погрешность средства измерения?

8. Что такое относительная погрешность средства измерения?

9. Что такое приведенная погрешность? Для каких целей она рассчитывается?

10. Что такое относительная погрешность средства измерения по входу и по выходу?

11. Что такое инструментальная погрешность средства измерения?

12. Что такое методическая погрешность?

13. Что такое систематическая и прогрессирующая погрешности средств измерений?

14. Что такое аддитивная погрешность средства измерения?

15. Чем вызывается мультипликативная погрешность средства измерения?

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ:

Амперметром с диапазоном измерения от 0 до 50 А произведен ряд измерений (табл. 1):

Таблица 1

·  Произвести оценку результатов измерений (найти абсолютную, относительную и приведенные погрешности);

·  За нормирующее значение принять верхний предел шкалы.

Решение:

Истинное значение: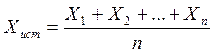

Абсолютная погрешность: Δ = ХД – Хист

Относительная погрешность: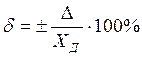

Приведенная погрешность: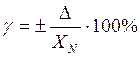

ВАРИАНТЫ ЗАДАЧ:

Задача 1:

Вольтметром с диапазоном измерения от 0 до 250 В произведен ряд измерений (табл. 1):

Таблица 1

·  Произвести оценку результатов измерений (найти абсолютную, относительную и приведенные погрешности);

·  За нормирующее значение принять верхний предел шкалы.

Задача 2:

Омметром с диапазоном измерения от 0 до 300 МОм произведен ряд измерений (табл. 1):

Таблица 1

·  Произвести оценку результатов измерений (найти абсолютную, относительную и приведенные погрешности);

·  За нормирующее значение принять верхний предел шкалы.

* Верхний предел измерений. Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа), называют соответственно «нижним пределом измерений» или «верхним пределом измерений».

* * Диапазон измерений — это область значений величины, в пределах кото­рой нормированы допускаемые пределы погрешности средства измерений.

* * * Длина шкалы — это длина линии, проходящей через центры всех коротких отметок шкалы средства измерений и ограниченной начальной и конечной отметками. Она выражается в единицах длины, независимо от единиц, указанных на шкале.