Понятие о расчётах на прочность

(эзс – 2 час, арх – 2 час, авто – 2)

1. Задачи сопротивления материалов — при проектировании зданий выбирают материалы и поперечные размеры конструкции: они должны быть такими, чтобы материал конструкции надёжно, без риска разрушиться сопротивлялся действию внешних сил.

2. Понятие о расчётах на прочность, жёсткость и устойчивость.

А) Прочность — способность конструкции выдерживать нагрузку без разрушения и остаточных деформаций.

Б) Жёсткость – способность конструкции сопротивляться упругим деформациям (способность не деформироваться, не прогибаться)

В) Устойчивость – способность конструкции сохранять первоначальную форму упругого равновесия.

3. Сопромат рассматривает тела, которые под действием внешних сил меняют свою форму и размеры, т. е. деформируются (в статике – абсолютно твёрдое тело, не деформируемое). Сопротивление материалов — раздел механики, называемый механикой деформируемых тел.

4. Упругие и пластические деформации.

а) упругие – если тело после устранения нагрузки, то есть внешних сил, восстанавливает свои размеры и форму;

б) остаточные — если тело после устранения нагрузки, то есть внешних сил, не восстанавливает свои размеры и форму.

5. Основные допущения о свойствах материалов.

А) материал однороден

Б) материал — сплошная среда и непрерывно заполняет объём элемента конструкции

В) материал изотропен, т. е. физико-механические свойства одинаковы по всем направлениям (древесина – не анизотропна)

Г) материал до определённых пределов обладает идеальную упругость, т. е. после снятия нагрузок тело полностью восстанавливает первоначальные формы и размеры.

6. Основные допущения о характере деформирования.

А) принцип начальных размеров – пренебрегать изменениями в расположении сил, т. е. исходят из первоначальной формы тела (элемента конструкции) и его начальных размеров.

Б) линейно-деформируемый характер деформации – перемещения точек упругого тела прямо пропорциональны силам, вызывающим эти перемещения.

В) принцип независимости действия сил – результат действия нескольких сил не зависит от последовательности нагружения ими данной конструкции и равен сумме результатов действия каждой силы в отдельности.

Нагрузки и их классификация

1. Виды нагрузок по способу их приложения к конструкции:

А) поверхностные:

— распределённые

— сосредоточенные

Б) объёмные (силы тяжести, силы инерции)

2. Виды нагрузок по характеру действия:

А) статические – медленно возрастают от нуля и остаются неизменными, достигнув конечного значения

Б) повторно-переменные (циклические) – многократно изменяются по времени по какому-нибудь периодическому закону (силы, действующие на зубья зубчатого колеса) – авто

В) динамические (ударные) – нагрузки, прикладываемые внезапно или с некоторой скоростью в момент контакта (забивание свай копром).

3. Основные расчётные схемы конструкций. Расчётная схема – реальный объект, освобождённый от несущественных особенностей.

а) пластина – параллелепипед – длина и ширина намного больше толщины;

б) оболочка – тело, ограниченное криволинейными поверхностями — длина и ширина намного больше толщины (как у пластины);

в) брус – тело, у которого размеры поперечного сечения малы по сравнению с его длиной. Прямой брус – если линия, соединяющая центры тяжести отдельных поперечных сечений бруса;

г) стержень – брус, работающий на растяжение или сжатие;

д) балка – брус, к которому силы приложены под углом – брус будет не только сжиматься и растягиваться, но и изгибаться

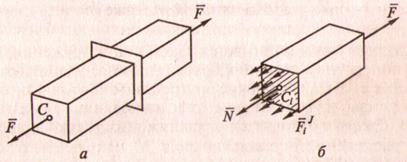
4. Метод сечений

А). В зависимости от того, какие силы приложены к телу, оно будет по-разному деформироваться.

Б). Для определения напряжённого состояния применяют метод сечений: тело мысленно рассекают плоскостью на две части и рассматривают равновесие одной из отсечённых частей

В). Считается, что внутренние силы распределены равномерно, их равнодействующая равна N

Г). Уравнение равновесия внешних и внутренних сил, действующих на отсечённую часть бруса

N – F = 0 N = F

5. Внутренние силовые факторы в общем случае нагружения бруса – все внутренние силы можно привести к главному вектору и главному моменту .

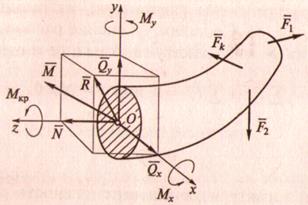
А) ось Z – направлена по нормали к сечению (по перпендикуляру)

Б) оси Ox и Оу – в плоскости сечения

В) внутренние силовые факторы:

—

— и у – составляющие поперечной силы

— Мкр – крутящий момент относительно оси Z

— Мх и Му – изгибающие моменты относительно осей Ox и Оу

определяют из 6 уравнений равновесия, составленных для отсечённой части бруса

6. Основные виды деформации бруса:

А) при действии одной силы — растяжение или сжатие

Б) при действии Мкр – кручение

В) при действии только Мх и Му – чистый изгиб

Г) при действии Мх (или Му) и поперечной силы Qу – поперечный изгиб

Д) сочетание внутренних силовых факторов вызывает сложное напряжённое состояние

7. Напряжение — интенсивность распределения внутренних сил по поперечному сечению.

Полное – в точке приложения можно разложить на два составляющих напряжения (векторы):

А) нормальное σ — интенсивность распределения внутренних сил по нормали к сечению

σ = NS

S — площадь поперечного сечения

N – равнодействующая внутренних нормальных сил

Б) касательное τ — интенсивность распределения внутренних сил, лежащих в плоскости к сечению

τ = QS

Q – равнодействующая внутренних сил, лежащих в плоскости сечения

8. Единицы измерения напряжения.

1 Па = 1Нм2

1 МПа = 1Нмм2

Самостоятельная работа обучающегося (эзс – 1 час, арх – 2 час, авто – 2)

1. Выполнить рабочий чертёж здания, указать и обозначить все действующие нагрузки (эзс, арх)

1. Подготовка сообщения по гипотезам и допущениям сопротив­ления материалов (авто)

ТЕМА 2.2. РАСТЯЖЕНИЕ И СЖАТИЕ (4.2. – АВТО)

(эзс – 4 час, арх – 2 час, авто – 2)

Понятие о сжатии и растяжении

1. Растяжение – вид нагружения, при котором в поперечном сечении бруса (стержня) возникают только нормальные силы, а прочие внутренние силовые факторы равны нулю: нормальная сила направлена от сечения

2. Сжатие отличается от растяжения только знаком силы и нормальная сила направлена к сечению

3. Сжатие, сопровождаемое изгибом – для длинных тонких стержней.

Закон Гука

1. Закон Гука определяет линейную зависимость между напряжением σ и деформацией ε (какова сила, такова и деформация)

σ = Е ε

2. Е – модуль упругости 1 рода, определяется экспериментально (в таблицах)

3. Для однородного тонкого стержня длиной l деформация ε

ε = ∆ l l

∆ l – удлинение стержня под действием приложенной силы

ε – деформация (относительное удлинение)

Удлинение стержня

1. Деформация – сумма силовой и температурной деформации

ε = σЕ + αt

α – коэффициент температурного расширения материала

t — температура

2. Деформация для однородного стержня, нагруженного по концам и равномерно нагретого

∆l = NlЕS + αlt

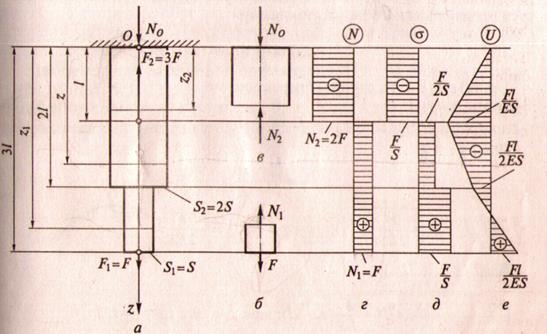
Построение эпюр (графиков)

1. Эпюра нормальных сил – график изменения нормальной силы стержня вдоль его оси

2. Эпюра напряжений – график изменения напряжений стержня вдоль его оси

3. Эпюра перемещений – график перемещений стержня вдоль его оси

Вывод: эпюры нужны для наглядности представления о законах изменения исследуемых величин