Понятие об устойчивых и неустойчивых формах равновесия

-поэтому более совершенна

— экспериментально получен критерий перехода от исследуемого напряжённого состояния А к эквивалентному В

— справедлив как для пластичных, так и для хрупких материалов

Пятая гипотеза (Бельтрами, 19в) – энергетическая гипотеза:

— гипотеза энергии формоизменения:

— критерий перехода от А к В основан на том, что

— предельное напряжённое состояние возникает при

— некотором значении потенциальной энергии

— накапливаемой элементом конструкции при изменении только его формы

→Самостоятельная работа обучающихся. (эзс – 5 час, арх – 6 час, авто – 2)

1. Выписать новые термины и коэффициенты в глоссарий.

2. Составить краткий алгоритм решения задач при расчете на прочность при косом изгибе и внецентренном сжатии

3. Построение эпюр нормальных напряжений по сечению при косом изгибе и внецентренном сжатии по вариантам

АВТО

1. Выполнение расчётно­-графической работы «Расчёт на проч­ность при сочетании основных видов деформаций»

2. Решение задач по расчёту вала цилиндрического косозубого редуктора на совместную деформацию изгиба и кручения

ТЕМА 2.8. УСТОЙЧИВОСТЬ ЦЕНТРАЛЬНО-СЖАТЫХ СТЕРЖНЕЙ (4.7. – АВТО)

(эзс – 4 час, арх – 1 час, авто – 1)

Понятие об устойчивых и неустойчивых формах равновесия. Критическая сила.

1. Устойчивость – свойство системы самостоятельно восстанавливать своё первоначальное положение после того, как ей было сообщено некоторое отклонение от положения равновесия.

2. Если система таким свойством не обладает, называется неустойчивой. (третья задача сопротивления материалов – расчёт на устойчивость (прочность, жёсткость – 1, 2 задачи)

3. В механике различают три состояния равновесия

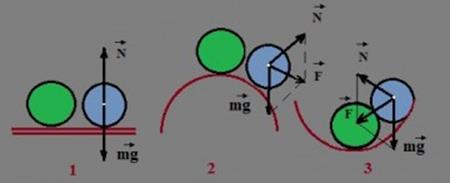
А) безразличное – при малом отклонении тело остаётся в равновесии. Пример: катящееся колесо, шар. Если их остановить в любой точке, оно окажется равновесии – рис.1.

Б) неустойчивое – при малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. Пример: шар в верхней точке – рис.2.

В) устойчивое – при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесие. Пример: шар в нижней точке – рис.3.

4. Потеря устойчивости – если упругое тело (конструкция) при отклонении от равновесия не возвращается к исходному положению. Явление потери устойчивости рассмотрим на примерах:

А) центрально-сжатого стержня — при некоторой продольно сжимающей силе стержень потеряет прямолинейную форму равновесия и изогнётся, иначе говоря, прямая форма равновесия становится неустойчивой.

Б) тонкостенной трубы – нагруженная внешним давлением: круговая форма становится неустойчивой и становится эллиптической, изогнувшись.

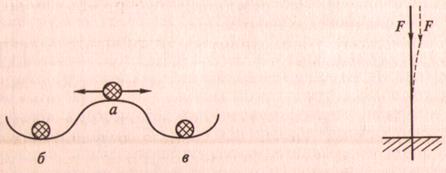
5. Критическая сила – максимальная сжимающая нагрузка Fкр, при которой прямолинейная форма стержня устойчива. (сила, при превышении которой происходит потеря устойчивости – критическое состояние)

Формула Эйлера при различных случаях опорных закреплений. Критическое напряжение.

1. Формула Эйлера для стержня длиной l, шарнирно закреплённого с двух сторон

Fкр = π2ЕJminl2

2. Формула Эйлера при различных случаях опорных закреплений

lпр = µl → Fкр = π2ЕJmin(µl)2

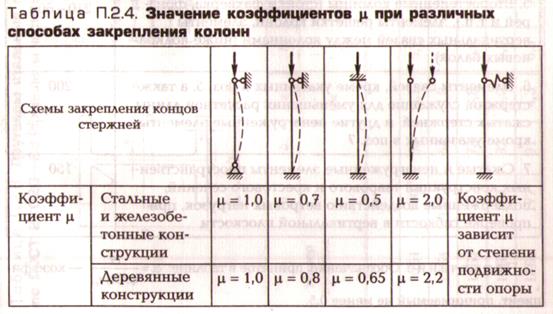
Вывод: значение критической силы зависит от способа закрепления его концов

3. Критические напряжения — нормальные напряжения, соответствующие критической силе, опасные для сжатого стержня. Критическая сила Fкр вызывает в сжатом стержне критическое напряжение σкр.

σкр = π2Е λ2

Гибкость – безразмерная величина, характеризует размеры стержня и способ закрепления концов

λ = µlimin

Пределы применимости формулы Эйлера

А) применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен.

λ ≥ λпред

λпред – предельная гибкость

Б) Как правило, многие конструкции имеют стержни с гибкостью меньше предельной

Формулы Ясинского. График критических напряжений в зависимости от гибкости.

1. Для стержней большой гибкости λ ≥ λпред критическое напряжение по формуле Эйлера.

σкр = π2Е λ2

2. Для стержней средней гибкости λо ≤ λ <λ пред Fкр по формуле Ясинского

σкр = а — b λ

Коэффициенты а, b – разные для разных материалов (определяют экспериментально)

3. Для стержней малой гибкости λ <λ о, для которых σкр соответствует σпред,

т. е. σкр = σт для пластичных материалов

σкр = σв. с. для хрупких материалов

Такие стержни рассчитывают не на устойчивость, а на прочность, как при простом сжатии

Расчёты на устойчивость сжатых стержней:

Условие устойчивости:

σ = FS [σу]

[σу] = σкрkу

[σу] — допускаемое напряжение на устойчивость

σкр – критическое напряжение

kу – коэффициент запаса на устойчивость

Самостоятельная работа обучающихся (эзс – 4 час, арх – 4 час, авто –1)

1. Решить задачи на определение критической силы для стержней большой гибкости по вариантам

2. Составить краткий алгоритм решения задач на определение критической силы для стержней большой гибкости

1. Решение задач по расчёту на устойчивость сжатых стержней — авто

ТЕМА 2.9. ПОНЯТИЕ О ДЕЙСТВИИ ДИНАМИЧЕСКИХ И

ПОВТОРНО-ПЕРЕМЕННЫХ НАГРУЗОК (4.9.АВТО)

(эзс – 2 час, арх – 1 час, авто – 3)

Основные понятия о действии динамических нагрузок

1. Статическая нагрузка – прикладывается без ускорения или с малым ускорением, которым можно пренебречь.

2. Динамическая нагрузка:

А) возникает при изменении скорости приложения нагрузки (груза) за очень короткий промежуток времени, т. е. ускоренно.

Б) часто нагрузки динамические, так как изменяются во времени с большой скоростью.

В) действие таких нагрузок сопровождается колебаниями сооружений и их отдельных элементов.

3. Усилия, напряжения и перемещения для динамических нагрузок больше и опаснее.

4. Виды динамических нагрузок:

А) инерционные – груз ускоренно поднимается вверх, оказывая динамическое воздействие на трос;

Б) ударные – груз падает с некоторой высоты (например, на плиту). Аналогичная нагрузка – при забивке сваи копром.

В) подвижные – перемещение поезда по мосту

Г) переменные или повторно-переменные (циклические) – действуют на элемент конструкции периодически, многократно изменяясь во времени по величине и по направлению. Пример: для отделения куска проволоки от мотка – сгибаем его в разном направлении в одном месте → знакопеременные нагрузки → усталостные разрушения → от удлинений, укорочений, прогибов, сдвигов.

5. В машинах и механизмах встречаются все виды динамических нагрузок. Они характерны для многих машиностроительных конструкций — оси, валы, штоки, пружины, шатуны и т. д – авто.

5. В строительстве чаще встречаются инерционные и ударные нагрузки

Понятие об усталости

1. Нагрузки, циклически изменяющиеся во времени по величине или по величине и по знаку, могут привести к разрушению конструкции при напряжениях, существенно меньших, чем предел текучести (или предел прочности).

2. Такое разрушение принято называть «усталостным». Материал как бы «устает» под действием многократных периодических нагрузок.

3. Усталостное разрушение – разрушение материала под действием повторно — переменных напряжений.

4. Усталость материала – постепенное накопление повреждений в материале под действием переменных напряжений, приводящих к образованию трещин в материале и разрушению.

5. Выносливость – способность материала сопротивляться усталостному разрушению.

6. Предел выносливости (пре­дел усталости) — наибольшее значение максимального по величине напряжения цикла, которому материал может сопротивляться без разрушения неограни­ченно долго.

 7. Виды усталости:

А) многоцикловое усталостное раз­рушение, характеризуемое повреждением и разрушением материала за большое число циклов нагружения (более 105) при напряжениях, мень­ших предела текучести материала.

Б) малоцикловая усталость, которая наблюдается при относительно малом числе циклов (порядка 103…105), когда действующие напряжения вызывают упругопластические дефор­мации, что характерно для высоконапряженных конструкций.

Расчеты деталей сооружений на динамические нагрузки

1. Расчёт более сло­жный, чем на статическую нагрузку:

А) сложнее методы определения внутренних усилий и напряжений от динамической на­грузки

Б) сложнее методы определения меха­нических свойств материалов при динамической нагрузке.