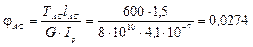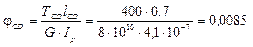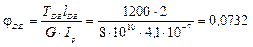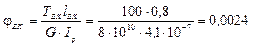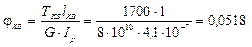Последовательность расчета статически неопределимых систем

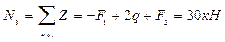
Строим эпюру нормальной силы (рис. 4)

Определяем удлинение стержня

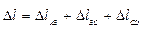
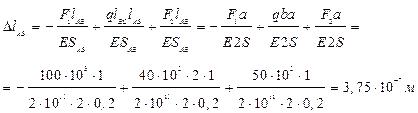
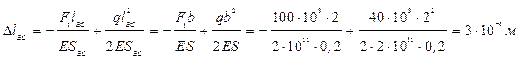
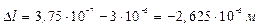
Указания к задаче 3

Стержневая система, рассматриваемая в данной задаче, относится к статически неопределимым системам, в которых невозможно определить усилия в стержнях только при помощи уравнений статики, так как число неизвестных усилий превышает число уравнений статики. При решении задач со статически неопределимыми системами приходится составлять дополнительные уравнения, которые называются уравнениями совместности деформаций. После того, как дополнительные уравнения будут составлены, их решают вместе с имеющимися уравнениями статики, то есть проводят синтез.

Последовательность расчета статически неопределимых систем

Чтобы решить статически неопределимую систему необходимо раскрыть статическую неопределимость.

1. Найти степень статической неопределимости.

,

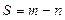где m — число неизвестных усилий;

n – число уравнений статики.

2. Статическая сторона задачи.

Рассматривает все возможные уравнения статики.

; ; .

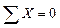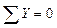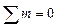3. Геометрическая сторона задачи.

Рассматривает деформированное состояние системы и связывает между собой деформации или перемещения отдельных точек. Эти уравнения называются уравнениями совместности деформаций.

4. Физическая сторона задачи.

Через закон Гука связывает между собой неизвестные усилия и деформации, вызванные этими усилиями.

5. Синтез.

Решая совместно полученные в пунктах 2,3,4 уравнения, раскрываем статическую неопределимость и решаем поставленную задачу.

Примечание. При изменении температуры, рассматривая физическую сторону задачи, кроме деформаций, вызванных нагрузками, нужно учитывать деформации, вызванные изменением температуры.

ПРИМЕР

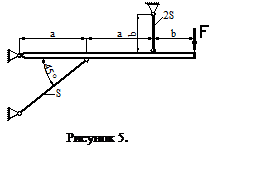Для схемы, изображенной на рис. 5 необходимо:

1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную или неравнополочную сталь, при условии, что поперечное сечение одного из стержней в два раза больше, чем другого.

2) Определить напряжения в стержнях:

—  от действия силы F;

—  от неточности монтажа, если считать, что один из стержней выполнен короче на величину D;

—  от изменения температуры.

3) Определить суммарные напряжения от действия внешних сил, от неточности монтажа и от изменения температуры.

4) Подсчитать недонапряжения или перенапряжения в стержнях.

Дано: F=100кН, а = 1,2м, b = 0,8м, D = 0,2мм, Dt = 20°С, Е = 2×105МПа, a = 125×10-71/гр, [s] = 100МПа.

Решение.

Для определения необходимой по условию прочности площади поперечного сечения стержней обратимся к рис. 6.

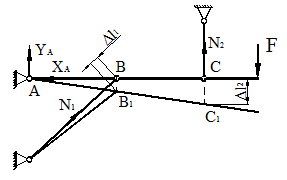
Рисунок 6.

1)  Находим степень статической неопределимости.

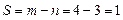
2.1) Статическая сторона задачи

; ;

; ;

; .

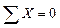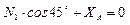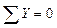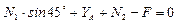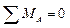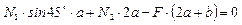2.2) Геометрическая сторона задачи

~ Þ

; ; ;

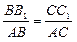
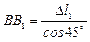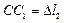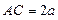
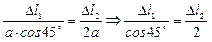
2.3) Физическая сторона задачи

;

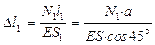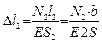
2.4) Синтез

Подставим выражения, полученные в физической стороне задачи, в выражения из геометрической стороны задачи и приведем подобные.

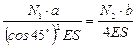
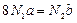
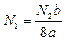
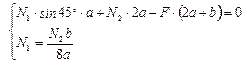Решим совместно систему уравнений, составленную из полученного выражения для N1 и уравнения моментов из статической стороны задачи.

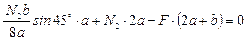
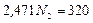
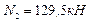
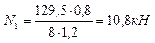
2.5) Определяем площадь поперечного сечения стержней

Определим, какой из стержней нагружен сильнее.

;

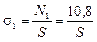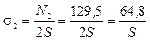
Второй стержень является более нагруженным, так как s2>s1, поэтому запишем для него условие прочности и определим площадь поперечного сечения.

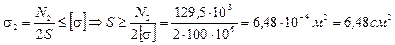
Подбираем по справочнику угловую равнополочную сталь № 70´5 ГОСТ8509-86 (SТ = 6,86 см2).

2.6) Определяем напряжения в стержнях от внешних сил

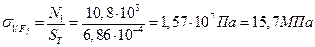
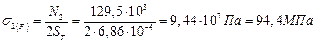
Первый стержень работает на сжатие, а второй – на растяжение.

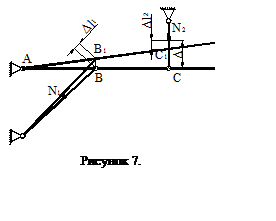
3) Определим напряжения в стержнях от неточности монтажа

Будем считать, что короткий стержень выполнен короче на величину D (рис. 7).

3.1) Статическая сторона задачи

; ;

; ;

; .

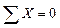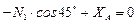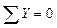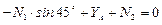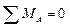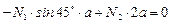3.2) Геометрическая сторона задачи

~ Þ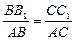

; ; ;

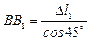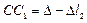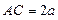
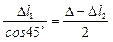
3.3) Физическая сторона задачи

;

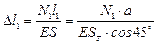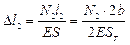
3.4) Синтез

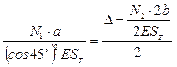
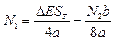
Подставим в полученное выражение данные из условия задачи и получим:

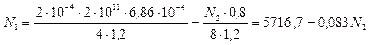
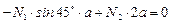
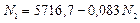
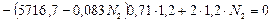
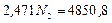
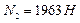
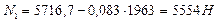
3.5) Определим напряжения в стержнях

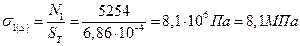
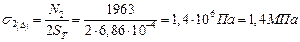
Оба стержня работают на растяжение.

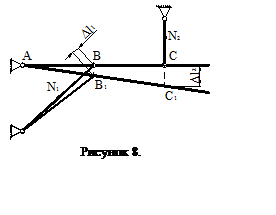
4) Определим напряжения в стержнях от изменения температуры (рис. 8).

Будем считать, что температура системы повышается. Тогда оба стержня будут удлиняться от повышения температуры. При удлинении стержней, они будут воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях будут возникать дополнительные силы сжатия.

4.1) Статическая сторона задачи

; ;

; ;

; .

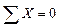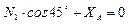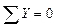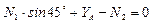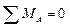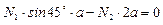4.2) Геометрическая сторона задачи

~ Þ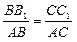

; ; ;

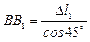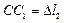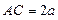
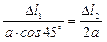
4.3) Физическая сторона задачи

; .

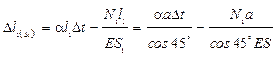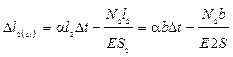4.4) Синтез

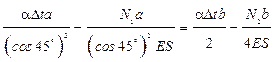
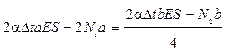
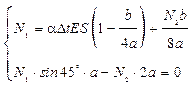
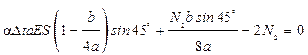
Решив уравнение, получим .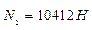

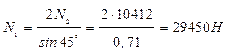
4.5) Определим напряжения в стержнях

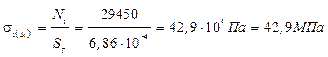
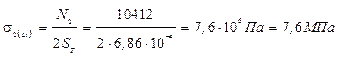
Оба стержня работают на сжатие.

5) Определим суммарные напряжения в стержнях

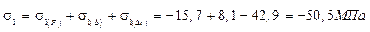
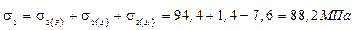
6) Найдем недонапряжения или перенапряжения в стержнях

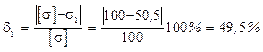— недонапряжение

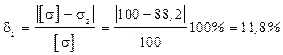— недонапряжение.

Указания к задаче 4

Кручение – это такой вид деформации стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент.

Внешние моменты, воздействующие на вал, называются скручивающими.

Расчет вала на прочность начинается с построения эпюры крутящего момента и отыскания опасного сечения.

Касательные напряжения при кручении определяются по формуле:

,

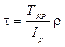где ТКР – крутящий момент, действующий в сечении;

r — радиус той точки поперечного сечения, в которой определяются напряжения;

Ip – полярный момент инерции сечения.

Условие прочности при кручении записывается следующим образом:

.

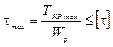где Wp – полярный момент сопротивления сечения.

Угол закручивания вала определяется по формуле:

,

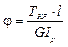где l – длина вала;

G – модуль упругости второго рода.

Условие жесткости при кручении записывается следующим образом:

.

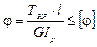Полярный момент инерции и полярный момент сопротивления круглого сечения определяются по формулам соответственно:

, ,

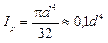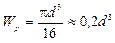где d – диаметр вала.

Полярный момент инерции и полярный момент сопротивления кольцевого сечения определяются по формулам соответственно:

, ,

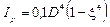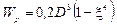где D – внешний диаметр вала;

;

d – внутренний диаметр вала.

ПРИМЕР

Для вала, изображенного на рис. 9, подобрать поперечное сечение круглой, кольцевой и прямоугольной форм, если Т1 =600 Нм, Т2 =1000 Нм, Т3 = =800Нм, Т4 = 1300 Нм, Т5 =1600Нм, x = 0,7, h/b = 2, [t] =100МПа. Построить эпюру углов закручивания для вала круглого поперечного сечения.

Решение

1)  Строим эпюру крутящего момента со свободного конца вала и определяем опасное сечение

АС

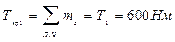
СД

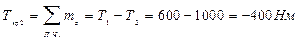
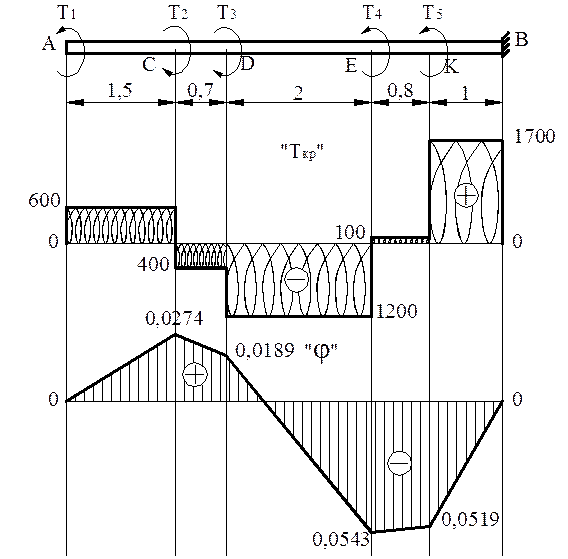
Рисунок 9.

ДЕ

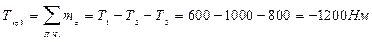
ЕК

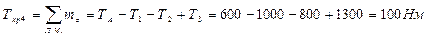
КВ

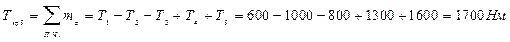
Из эпюры крутящих моментов (рис. 9) видно, что опасным, является участок КВ, максимальное значение крутящего момента Ткр max= 1700 Нм.

2)  Подбираем поперечное сечение вала

7.1) Круглое сечение

Условие прочности при кручении:

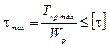
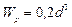
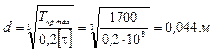
Принимаем d = 45 мм.

7.2) Кольцевое сечение

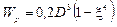
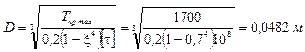
Принимаем D = 50 мм, тогда 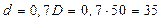мм.

7.3) Прямоугольное сечение

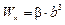
Для прямоугольного сечения с отношением h/b = 2 b = 0,493.

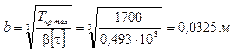
Тогда 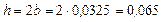м.

3)  Строим эпюру углов закручивания

Найдем момент инерции для круглого сечения:

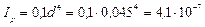м4.