Преобразования лоренца для напряженности полей и потенциалов

Из самого определения этого тензора следует, что он антисимметричен. Антисимметричные тензоры и их основные свойства были достаточно подробно обсуждены выше.

Сейчас запишем компоненты тензора . Так как тензор антисимметричен, то сразу можно написать, что

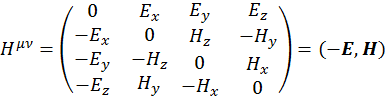(1.10.2)

Здесь E — напряженность электрического поля, а H — напряженность магнитного поля.

Оказывается, что все компоненты тензора можно вывести напрямую из его определения, и в результате получим:

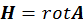(1.10.3)

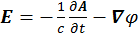(1.10.4)

Мы получили тензор напряженности электромагнитных полей. Иногда в электродинамике используется другой тензор электромагнитного поля, называемый дуальным к основному тензору или дуальным тензором. Дуальный тензор связан с основным следующим соотношением:

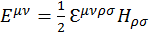(1.10.5)

где — все тот же символ Леви-Чевита.

Исходя из определения, дуальный тензор имеет вид:

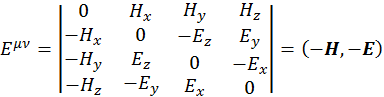(1.10.6)

Проверим некоторые компоненты этого тензора:

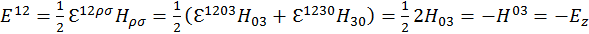(1.10.7)

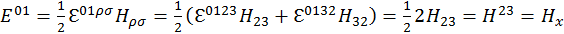(1.10.8)

Можно написать обратное преобразование

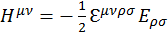(1.10.9)

В общем виде проверка этого соотношения выглядит следующим образом

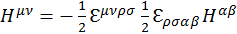
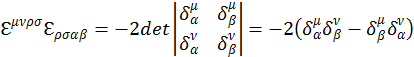
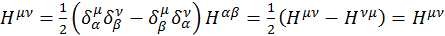(1.10.10)

§ 1.11. Преобразования Лоренца для напряженности полей и потенциалов

Как мы уже знаем, четырехмерный вектор преобразуется по закону:

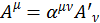. (1.11.1)

Мы уже показали, что

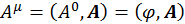(1.11.2)

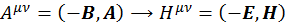. (1.11.3)

Фактически все сводится к замене

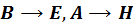. (1.11.4)

Таким образом, мы имеем следующую замену переменных:

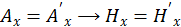
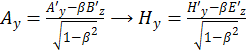(1.11.5)

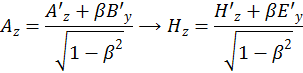
А также

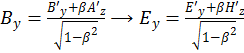(1.11.6)

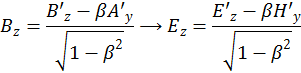
Эти формулы можно записать в трехмерном векторном виде

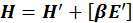. (1.11.7)

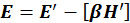(1.11.8)

§ 1.12. Инварианты электромагнитного поля

Тензоры второго ранга имеют инварианты вида:

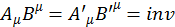(1.12.1)

Это легко можно показать, расписывая тензоры по определению. Наша задача состоит в том, чтобы найти инварианты электромагнитного поля.

Мы знаем только два тензора электромагнитного поля:

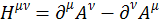(1.12.2)

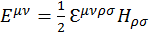(1.12.3)

Из этих двух тензоров можно построить два различных инварианта. Докажем это.

Возможны три комбинации:

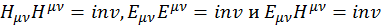(1.12.4)

Для начала вычислим первый инвариант, опуская дословное описание суммирования по каждому из индексов и :

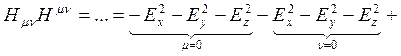
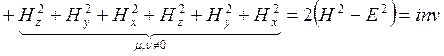. (1.12.5)

То есть, для первого инварианта можно записать:

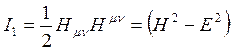. (1.12.6)

Аналогично можно вычислить и второй инвариант:

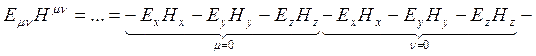
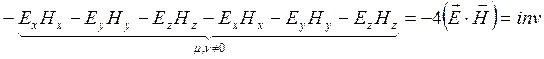. (1.12.7)

Второй инвариант выглядит как:

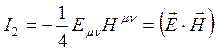. (1.12.8)

Третий инвариант нет смысла высчитывать, т. к. он будет равен первому инварианту. Таким образом, из трех комбинаций осталось две независимых, которые и будут инвариантами электромагнитного поля.

Рассмотрим некоторые следствия из этих инвариантов.

1.  Если в одной инерциальной системе отсчета E<H (E>H), то и в любой другой инерциальной системе отсчета E′<H′ (E′>H′). Если в одной инерциальной системе отсчета E=H, то и в любой другой инерциальной системе отсчета E′=H′.

Данные утверждения следуют из первого инварианта.

2.  Если в одной инерциальной системе отсчета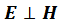, то и в любой другой инерциальной системе отсчета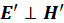

Если cosα>0, то угол между E и H будет острым, если cosα<0 то угол α — тупой.

Если угол между E и H острый или тупой в одной инерциальной системе отсчета, то он будет острым или тупым в любой другой инерциальной системе отсчета.

Это вытекает из скалярного произведения во втором инварианте:

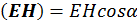(1.12.9)