Применение теории взаимодействия магнитного момента

В точке, где находится, заряд вектор напряженности можно выразить следующим образом:

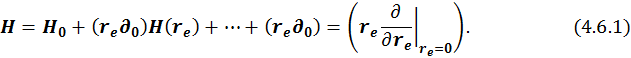
Полная сила, действующая на всю систему, вычисляется как сумма сил действующих на произвольно выбранный нами заряд :

где -скорость заряда e.

Подставим значение вектора напряженности в выражение (4.6.2):

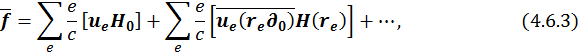
где определяется также как и в (4.4.4).

По теореме о среднем первый член выражения (4.6.3) равен нулю. Аналогично вычисленному в предыдущем параграфе выражению:

мы можем записать:

Тогда для силы действующей на всю систему мы можем записать:

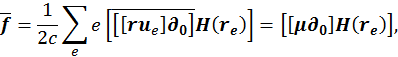
где – магнитный дипольный момент системы:

В выражении (4.6.4) действует только на координаты наблюдателя:

Учитывая, что

полная сила принимает следующий вид:

В механике Ньютона сила выражается через потенциальную энергию (при j=o):

таким образом, сравнив два выражения мы можем записать:

Также, формула для силы может быть записаны в виде функции Штерна и Герлаха:

где согласно (3.4.11) .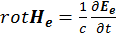

Т. к. мы рассматриваем систему во внешнем магнитном поле (без участия электрического), выражение для силы, действующей на нашу систему примет вид:

Отсюда видно, что если внешнее поле является однородным, то полная сила, действующая на систему равна нулю.

Далее рассмотрим однородное магнитное поле и найдем значение момента сил действующих на систему.

Момент сил, для системы частиц, которые взаимодействуют только друг с другом, при отсутствии внешнего магнитного поля выражается следующей формулой:

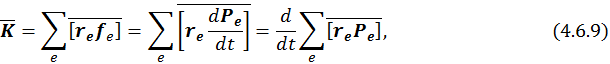
используя терему о среднем мы получим:

Т. о. можно сделать вывод, что при отсутствии внешнего поля момент сил равен нулю. Но при наличии воздействия извне картина существенно изменится, возникает сила Лоренца:

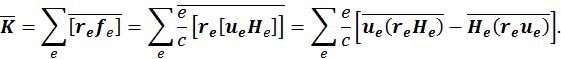
Если рассматриваемое поле однородно, то оно одинаково во всех точках, где находятся заряды, тогда по теореме о среднем второй член равен нулю, таким образом:

используя, ранее выведенную формулу, получим окончательное выражение для момента сил:

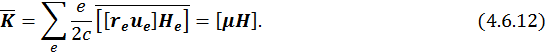
§ 4.7. Применение теории взаимодействия магнитного момента с внешним магнитным полем

а) Диамагнетизм электронной плазмы.

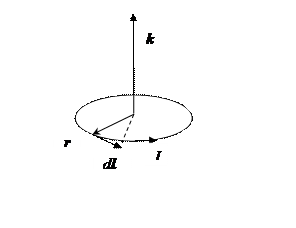
Согласно общему определению магнитного момента системы, в случае одноэлектронного витка с током, магнитный момент можно записать в виде:

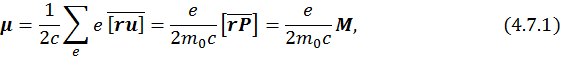
где — механический момент системы, связанный с движение самого заряда, — импульс для одноэлектронного витка с током.

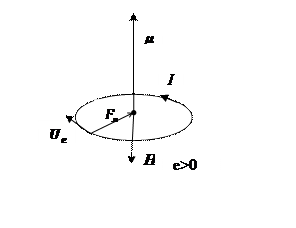
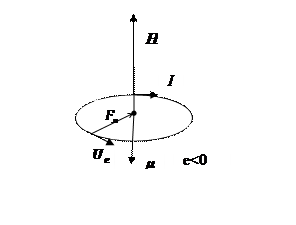
Из выражения видно, что параллельность и антипараллельность моментов определяется знаком заряда частицы.

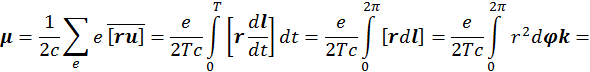
где 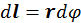— малый участок траектории, — площадь окружности, —единичный вектор, ортогональный плоскости витка с током. Магнитный момент в этом случае параллелен механическому моменту.

Выразим величину магнитного момента через напряженность внешнего магнитного поля:

Умножим и разделим это выражение на круговую частоту 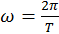, и введем -линейная скорость кругового движения, тогда:

Рассмотрим нерелятивистский случай (), учитывая, что круговая частота имеет следующий вид:

Мы получим, что величина магнитного момента не зависит от заряда: